JAVA [자바] - 소수 구하는 알고리즘 및 구현
- 들어가기 전에
소수 [Prime Number]
소수의 정의는 1보다 큰 자연수 중 1 과 그 수 자기 자신만을 약수로 갖는 자연수를 의미한다는 점은 누구나 알고 있을 것이다.
즉, 소수의 약수는 2개만을 갖고, 그 중 하나는 반드시 1 이며, 나머지는 자기 자신만을 약수로 갖기 때문에 만약 1 보다 크고 자기 자신의 수보다 작은 자연수를 약수로 갖게 된다면 이는 합성수라고 한다.
그리고 위의 개념을 확장해본다면 합성수는 3개 이상인 자연수의 곱으로 이루어져 있으며 소수로 이루어진 곱으로 표현할 수 있다.
그리고 이를 소인수분해라고 한다.
더욱 개념을 넓혀볼까.
소수는 1과 자기 자신만을 약수로 갖고, 합성수는 3개 이상인 자연수의 곱으로 이루어져 있으며 소수들로 이루어진 곱으로 표현할 수 있다고 했다.
1 보다 큰 자연수는 모두 소수 또는 합성수로 이루어져 있으니 1 보다 큰 모든 자연수는 소수들의 곱으로 표현할 수 있다.
이렇듯 소수는 수학적으로도 매우 중요한 개념이다.
그렇다면 왜 개발자 입장에서 또는 프로그래밍의 세계에서 소수가 중요한 이유는 무엇일까.
바로 "암호" 때문이다.
실제로 우리 일상생활에서도 많이 쓰이는 암호 또한 소수를 이용하고 있다.
대표적으로 'RSA 암호화 방식'이 있다.
위 암호화 방식의 가장 근본적인 접근 방식은 이렇다.
"임의의 수들의 곱은 구하기 쉽지만 역으로 소인수 분해하는 것은 어렵다."
즉, 𝑝 × 𝑞 = 𝐍 를 만들기는 쉽지만, 𝐍 을 역으로 소인수 분해하여 𝑝 × 𝑞 를 만족하는 수를 찾기가 어렵다는 것이다.
예로 들어보자.
77 을 소인수분해 하면?
7 × 11 이 바로 나온다.
그렇다면 조금 더 큰 수라면 어떨까?
12126 을 소인수 분해 해보자.
먼저 직관적으로는 2로 나누어 떨어지겠다.
P × 2 = 12126 ... P = 6063
그리고 각 자릿수의 합 ( 6 + 0 + 6 + 3 ) 은 15 로 3의 배수이니 3으로 나누어 떨어지겠다.
P × 2 × 3 = 12126 ... P = 2021
그리고 2021 이 수를 소인수 분해를 해보자.
한 번에 눈에 들어오는가?
2021 을 소인수 분해하면 43 과 47 이다.
즉, 2부터 하나씩 대입해보려 하면 43 까지 대입해보아야 한다.
그리고 43과 47 은 각각 소수로 더이상의 소인수분해가 불가능 하다.
뭐 이정도 까진.. 컴퓨터의 대단한 연산능력에 맏기면 금방 풀릴 수 있겠다.
그런데 다음과 같은 수라면??
114381625757888867669235779976146612010218296721242362562561842935706935245733897830597123563958705058989075147599290026879543541
이 수는 실제로 RSA-129 의 공개키였고 현재는 풀린 129자리의 수다.
위 수를 여러분의 컴퓨터로 소인수 분해를 할 수 있겠는가?
일단 정답부터 말하자면 다음과 같다.
RSA-129 =
3490529510847650949147849619903898133417764638493387843990820577 × 32769132993266709549961988190834461413177642967992942539798288533
위의 두 수는 반드시 소수다.
위 문제를 컴퓨터로 푼다면 쉽게 풀릴 것 같지만 이는 오산이다.
실제로 위 문제를 풀기위해서 약 1600대의 컴퓨터와 600명의 사람이 모여 6개월동안 진행했다.
이 마저도 129자리 소수를 푸는데 저러한 시간이 걸렸는데 현재 암호방식은 RSA-2048로 617 자리수의 공개키가 있다.
617 자리의 수는 얼마나 오래 걸릴지 가늠이 안된다.
그래서 실제로도 대부분의 인터넷뱅킹도 RSA-2048 을 쓰고 있다.
혹시 독자 분들 중에 위 키를 푼다면 혹시 모를까... 세계 유명인사가 될 테니..
RSA-2048 의 공개키를 공유하겠다.
RSA-2048 =
25195908475657893494027183240048398571429282126204032027777137836043662020707595556264018525880784406918290641249515082189298559149176184502808489120072844992687392807287776735971418347270261896375014971824691165077613379859095700097330459748808428401797429100642458691817195118746121515172654632282216869987549182422433637259085141865462043576798423387184774447920739934236584823824281198163815010674810451660377306056201619676256133844143603833904414952634432190114657544454178424020924616515723350778707749817125772467962926386356373289912154831438167899885040445364023527381951378636564391212010397122822120720357
(화이팅입니다...)
서론이 너무 길었다.. 여튼 소수는 우리 일상생활에서도 긴밀하게 쓰이고 있다.
그런김에 소수를 구하고 판별하는 몇가지 방법을 같이 배워보고자 한다.
각 방법마다 소수를 판별하는 알고리즘과,
N 이하의 소수를 모두 구하는 알고리즘을 소개하겠다.
- 방법 1
" N 보다 작은 자연수들로 모두 나눠본다. "
가장 기본적인 방법이라 할 수 있겠다.
임의의 수 N 이 1 과 N 을 제외한 다른 수를 약수로 갖고 있다면 그 수는 소수가 아니고, 만약 다른 약수가 없다면 그 수는 소수일 것이다.
[ 소수 판별 알고리즘 ]
import java.util.Scanner;
public class Prime_1 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
is_prime(in.nextInt());
}
// 소수 판별 메소드
public static void is_prime(int number) {
// 0 과 1 은 소수가 아니다
if(number < 2) {
System.out.print("소수가 아닙니다");
return;
}
// 2 는 소수다
if(number == 2) {
System.out.print("소수입니다");
return;
}
for(int i = 2; i < number; i++) {
// 소수가 아닐경우
if(number % i == 0) {
System.out.print("소수가 아닙니다");
return;
}
}
// 위 반복문에서 약수를 갖고 있지 않는경우 소수다.
System.out.print("소수입니다");
return;
}
}
2 이상 N 미만의 수 중에 나누어 떨어지는 수가 존재한다면 소수가 아님을 이용한 소수 판별법이다.
또한, 위 알고리즘의 시간복잡도는 당연히 N 이하의 수까지 모든 수를 검사하므로 O(N) 이다.
[ N 이하의 모든 소수 구하는 알고리즘 ]
위를 응용하여 N 이하의 소수를 모두 구하는 알고리즘은 다음과 같을 것이다.
// 소수만 출력
import java.util.Scanner;
public class Prime_1 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
// 0 ~ N 까지 수 중 소수를 구하는 반복문
for(int i = 0; i <= N; i++) {
make_prime(i);
}
}
// 소수 생성 메소드
public static void make_prime(int number) {
// 0 과 1 은 소수가 아니므로 종료
if(number < 2) {
return;
}
// 2 는 소수다
if(number == 2) {
System.out.println(number);
return;
}
for(int i = 2; i < number; i++) {
// 소수가 아닐경우 종료
if(number % i == 0) {
return;
}
}
// 위 반복문에서 약수를 갖고 있지 않는경우 소수다.
System.out.println(number);
return;
}
}
위 알고리즘은 소수 판별 알고리즘을 N 번 반복하여 각 수마다 소수 판별 한 뒤 소수만 출력하도록 한 알고리즘이다.
즉 O(N) 알고리즘을 N 번 반복하므로 위 방법의 N 이하의 소수를 모두 구하는 알고리즘의 시간복잡도는 O(N²) 이다.
- 방법 2
" √N 이하의 자연수들로 모두 나눠본다. "
방법 1 의 방법에서 약간 업그레이드 된 알고리즘이다.
바로 N 을 √N 이하의 자연수들만 나누는 방법이다.
왜 √N 이하의 자연수들만 나누면 되는지는 생각보다 매우 쉽게 알 수 있다.
생각해보자. 소수를 판별한다는 것은 결국 1 과 자기 자신을 제외한 다른 자연수를 약수로 갖고 있으면 안된다는 의미다.
임의의 자연수 𝐍 (𝐍 > 0) 이 있다고 가정하자.
𝑝 × 𝑞 = 𝐍 을 만족할 때 우리는 아래와 같은 부등식을 완성할 수 있다.
( 1 ≤ 𝑝 , 𝑞 ≤ 𝐍 )
그리고 𝑝 와 𝑞 중 하나는 √N 보다 작거나 같다.
예로들어 𝐍 = 16 라고 하자.
그러면 아래와 같이 두 수의 곱으로 표현할 수 있다.
1 × 16
2 × 8
4 × 4
8 × 2
16 × 1
여기서 볼 수 있듯이 만약 𝑝 가 증가한다면 자연스레 𝑞 가 감소하고,
반대로 𝑝 가 감소한다면 자연스레 𝑞 가 증가한다.
그리고 𝑝 와 𝑞 는 𝐍의 약수이기 때문에 결국 𝐍 을 임의의 수로 나누게 되면 임의의 수가 √N 보다 작다면 결국 나머지는 √N 보다 클 수 밖에 없다.
결과적으로 𝑝 와 𝑞 중 하나는 반드시 √N 보다 작거나 같다.
즉, √N 이하의 자연수 중에 나누어 떨어지는 수가 있다면 이는 1 과 N 을 제외한 다른 자연수가 N 의 약수라는 의미이므로 소수가 아니게 되는 것이다.
그럼 이를 토대로 알고리즘을 짜보자.
[ 소수 판별 알고리즘 ]
import java.util.Scanner;
public class Prime_2 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
is_prime(in.nextInt());
}
// 소수 판별 메소드
public static void is_prime(int number) {
// 0 과 1 은 소수가 아니다
if(number < 2) {
System.out.print("소수가 아닙니다");
return;
}
// 2 는 소수다
if(number == 2) {
System.out.print("소수입니다");
return;
}
// 제곱근 함수 : Math.sqrt()
for(int i = 2; i <= Math.sqrt(number); i++) {
// 소수가 아닐경우
if(number % i == 0) {
System.out.print("소수가 아닙니다");
return;
}
}
// 위 반복문에서 약수를 갖고 있지 않는경우 소수다.
System.out.print("소수입니다");
return;
}
}
2 이상 √N 이하의 수 중에 나누어 떨어지는 수가 존재한다면 소수가 아님을 이용한 소수 판별법이다.
또한, 위 알고리즘의 시간복잡도는 당연히 √N 이하의 수까지 모든 수를 검사하므로 O(√N) 이다.
[ N 이하의 모든 소수 구하는 알고리즘 ]
위를 응용하여 N 이하의 소수를 구하는 알고리즘은 다음과 같을 것이다.
// 소수만 출력
import java.util.Scanner;
public class Prime_2 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
// 0 ~ N 까지 수 중 소수를 구하는 반복문
for(int i = 0; i <= N; i++) {
make_prime(i);
}
}
// 소수 생성 메소드
public static void make_prime(int number) {
// 0 과 1 은 소수가 아니므로 종료
if(number < 2) {
return;
}
// 2 는 소수다
if(number == 2) {
System.out.println(number);
return;
}
// 제곱근 함수 : Math.sqrt()
for(int i = 2; i <= Math.sqrt(number); i++) {
// 소수가 아닐경우 종료
if(number % i == 0) {
return;
}
}
// 위 반복문에서 약수를 갖고 있지 않는경우 소수다.
System.out.println(number);
return;
}
}
위 알고리즘은 소수 판별 알고리즘을 N 번 반복하여 각 수마다 소수 판별 한 뒤 소수만 출력하도록 한 알고리즘이다.
즉 O(√N) 알고리즘을 N 번 반복하므로 위 방법의 N 이하의 소수를 모두 구하는 알고리즘의 시간복잡도는 O(N√N) 이다.
- 방법 3 : 에라토스테네스의 체
소수를 구하는 대표적인 방법 중 하나다.
" k=2 부터 √N 이하까지 반복하여 자연수들 중 k를 제외한 k의 배수들을 제외시킨다"
즉, 방법으로 보면 다음과 같다.
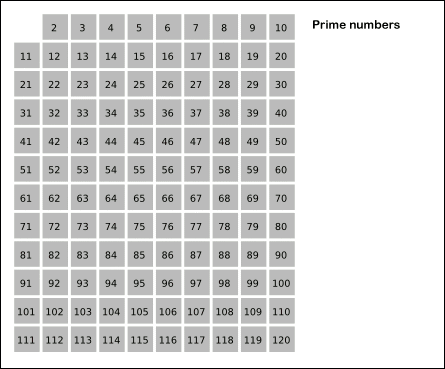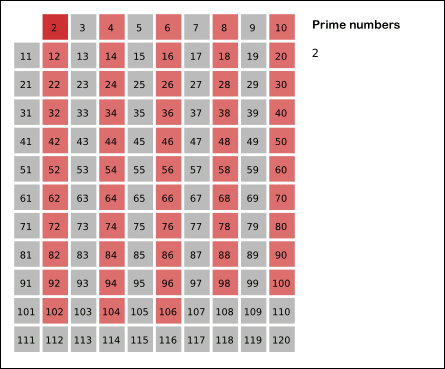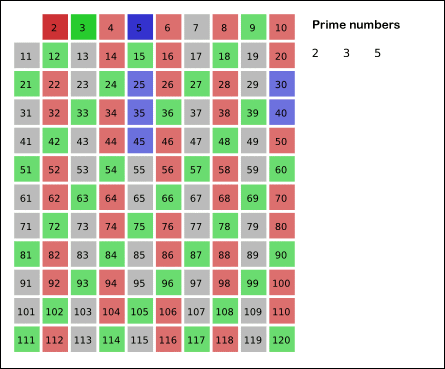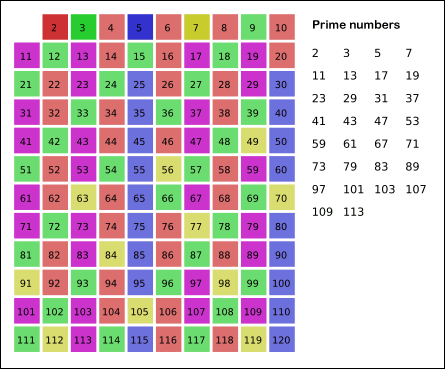
k = 2 이면 2 를 제외한 2의 배수를 모두 지워주고,
k = 3 이면 3 을 제외한 3의 배수를 모두 지워주고,
(4는 이미 k = 2 에서 제외되어 넘어간다.)
k = 5 이면 5 를 제외한 5의 배수를 모두 지워주고..
이렇게 하여 k = √N 까지 반복하는 방법이다.
이 방법은 소수를 구하는 방법이랑 판별하는 방법이 동일하기 때문에 하나로 묶어서 설명하겠다.
[ N 이하의 모든 소수를 구하는 알고리즘 ]
import java.util.Scanner;
public class Prime_3 {
public static boolean[] prime; // 소수를 체크할 배열
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
make_prime(N);
for(int i = 0; i < prime.length; i++) {
if(prime[i] == false) { // 소수(false)일 경우 출력
System.out.println(i);
}
}
}
// N 이하 소수 생성 메소드
public static void make_prime(int N) {
prime = new boolean[N + 1]; // 0 ~ N
/*
소수가 아닌 index = true
소수인 index = false
*/
// 2 미만의 N 을 입력받으면 소수는 판별할 필요 없으므로 바로 return
if(N < 2) {
return;
}
prime[0] = prime[1] = true;
// 제곱근 함수 : Math.sqrt()
for(int i = 2; i <= Math.sqrt(N); i++) {
// 이미 체크된 배열이면 다음 반복문으로 skip
if(prime[i] == true) {
continue;
}
// i 의 배수들을 걸러주기 위한 반복문
for(int j = i * i; j < prime.length; j = j+i) {
prime[j] = true;
}
}
}
}
언뜻 보기에는 이중for문이라 시간복잡도가 O(N²) 일 것 같지만 그렇지 않다.
1 ~ 𝑥 까지의 수가 있는 칸을 체크하는 횟수를 대략적으로 따진다면 아래와 같을 것이다.
(n = 1 부터 시작한다고 할 때)
(𝑥) + (𝑥/2) + (𝑥/3) + (𝑥/4) + (𝑥/5) + (𝑥/6) + ⋯ + 1
그러면 위 식을 다음과 같이 표현 할 수 있다.
𝑥(1 + 1/2 + 1/3 + ⋯ + 1/𝑥)
위의 x로 묶인 괄호 안의 수열은 조화 수(Harmonic Number)라고 하는데, 쉽게 말해서 조화 수열에서 부분 합을 말한다고 생각하면 된다.
그리고 다음과 같이 발산하게 된다고 한다.
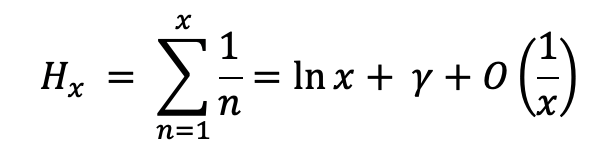
이 때 감마는 상수 값이고 O(1/x)는 우리가 생각하는 big O와 같은 표기로 수학에서는 함수 성장률의 상한선이다. 그리고 위의 조화수는 대략 자연로그의 형태를 따라간다.
(자세한 건 아래 링크를 참고하시기 바란다.)
https://en.wikipedia.org/wiki/Harmonic_number
즉, N 이하의 소수에 대하여 체에 거르는 시간이 logN 이므로 단순하게 체에 거르는 것만 해도 시간 복잡도는 O(N㏒N) 이다.
( ㏒ 는 자연로그 𝑙𝑛 으로 본다 )
그런데 우리는 여기서 더 나아가 이미 체크된 배열은 검사하지 않고 다음 반복문으로 넘어간다.
(𝑥/2) + (𝑥/3) + (𝑥/4) + (𝑥/5) + (𝑥/6) + (𝑥/7)+ (𝑥/8)+ (𝑥/9) + ⋯ + (𝑥/𝑥-1)
우리는 앞서 조화수를 통해 점근적 시간 복잡도 O(NlogN) 이라는 시간 복잡도를 얻었다.
이 의미는 x개의 수에 대해 2일 때 체크하는 개수인 (x/2), 3일 때 체크하는 개수인 (x/3), ... 이렇게 체크를 하게 된다.
하지만 우리가 알고싶은 것은 이미 중복되는 수들은 검사하지 않는다는 것이다. 이 의미는 무엇일까? 결국 검사하는 수는 소수로 판정 될 때 그의 배수들을 지우는 것이라는 것이다. 이 말은 구간 내의 소수의 개수를 알아야 한다는 뜻이기도 하다.
근데, 소수가 규칙성이 있는가? 이 것은 아직까지도 풀지못한 것이다. 이를 찾고자 가우스는 15살 때 하나하나씩 구하면서 x보다 작거나 같은 소수의 밀도에 대해 대략 1 / ln(x) 라는 것을 발견하게 되는데 증명을 못했다. (이를 가우스의 소수 정리라고 한다)
즉, 위를 거꾸로 말하면 x번째 소수는 xlog(x) 라는 의미가 되지 않겠는가? 즉, 우리는 앞서 1/x 의 합을 구했지만, 실제로 중복되는 수가 제외된다면 x는 소수만 된다는 의미고, 이는 소수의 역수 합이다. (1/2 + 1/3 + 1/5 + 1/7 + ⋯ ) 이런식으로 말이다.
그러면 시간 복잡도를 도출해낼 수 있다.
바로 O(Nlog(log N)) 의 시간 복잡도를 갖게 된다.
[소수에 대한 심화 내용]
이왕 소수 이야기가 나온김에 위에서 수식을 정리한 것을 이용하여 조금만 확장을 해보자.
앞서 구한 조화수를 다시 갖고와보자.
sum = (1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + ⋯ )
위 식을 T 라고 놓고 무한히 놓여있다는 가정하에 몇 가지 이리저리 만져보자.

그리고 위 식에서 1/2를 양변에 곱해보자.

그리고 (1)번 식에서 (2)번 식을 빼 보자.

이렇게 우변에 분모는 홀수만 남게 되었다.
그럼 분모 3에 대해서도 양변을 나눠서 해본다면 어떻게 될까? 다음과 같이 될 것이다.

이런식으로 진행하다보면 좌변에는 항상 (1 - (1/소수)) 만 오게 된다는 것을 알 수 있다.
즉, 모든 소수에 대해 위 과정을 반복하면 다음과 같은 등식이 나올 것이다.

그리고 위를 정리하면 다음과 같이 표현 할 수도 있다.

자 위 식의 경우 지수를 모두 -1으로 고정해놓고 정리했지만, 만약 지수도 어떤 집합 내의 수로 본다면 어떻게 정리할 수 있을까?
바로 다음과 같은 수식으로 정리할 수 있다.

만약 수학에 관심이 있는 분이라면 이 공식을 보면 뭔가 익숙하다는 느낌을 받을 수도 있을 것이다.
그렇다. 바로 리만-제타 함수 식다.

위 식에서 s를 복소수로 확장하면, 이 함수를 0으로 만드는 실수부는 1/2 이다. 라는 가설이 그 유명한 '리만 가설'이다. (솔직히 필자도 그렇다고만 알고있지 수학자가 아니라 자세하게는 모른다..)이에 대해 더 나아가면 필자도 모르는 내용이고 주제와는 완전 다른 곳으로 향할 것 같으니... 궁금한 분은 아래 유튜브를 참고하시기를 바란다. (필자가 본 수학 유튜버 중 가장 최고의 유튜버라고 생각한다..)
우리는 앞서 에라토스테네스의 체에서 가우스의 소수 정리 부분 중 소수 밀도라는 얘기를 잠깐 했었다. 여기서 하나 정의하고 있는 것이 바로 π(x) 라는 함수다. (소수 계량 함수라고도 한다.)
이 함수는 x 이하의 수 중 소수의 개수를 표현하는 함수라고 정의하고 있다. 예로들어 아래와 같다.
π(1) = 0, π(2) = 1, π(3) = 2, π(4) = 2 ...
그리고 앞서 소수 정리에서 x 이하의 수에 대해 어떤 정수가 소수일 확률, 즉 밀도는 1 / ln(x) 라고 했다.
즉, 위 가정이 맞다고 할 때, x까지의 모든 소수의 개수는 x / ln(x) 가 될 것이다.
그럼 π(x) 와 x / ln(x) 는 같아야 할 것이다. 즉, 아래와 같은 식이 될 것이다.

위 식이 바로 소수 정리의 메인이다. (x / ln(x) 를 로그 적분 함수로 li(x) 라고도 한다.)
하지만, x / ln(x) 즉, 분명하게 실제 소수의 개수인 π(x)와 li(x) 와는 차이가 존재한다. 바로 이 차이를 줄이는 것이 관건인 것이고 리만 제타 함수는 π(x) 를 구하기 위해 정의한 것이라고 보면 된다.
즉, 더욱 정확하게 소수의 분포를 알아내기 위해 나온 것이 리만 제타 함수고, 여기서 좀 더 확장하여 나온 하나의 가설이 바로 리만가설이라는 것이다. (복소평면에서 비자명근 어쩌고 저쩌고 하는데.. 사실 모두 이해하기에는 저도 너무 어렵네요..)
이렇게 잡지식을 하나 추가해보았다.
참고할만한 풀이 링크는 아래에 기재해두겠다.
How is the time complexity of Sieve of Eratosthenes is n*log(log(n))? - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
- 성능 분석
N 이하의 소수를 모두 구하는 시간 복잡도에 대해서 대락 아래와 같았다.
방법 1 : O(N²)
방법 2 : O(N√N)
방법 3 : O(N㏒(㏒N))
그래프로 보면 대략적으로 다음과 같다.
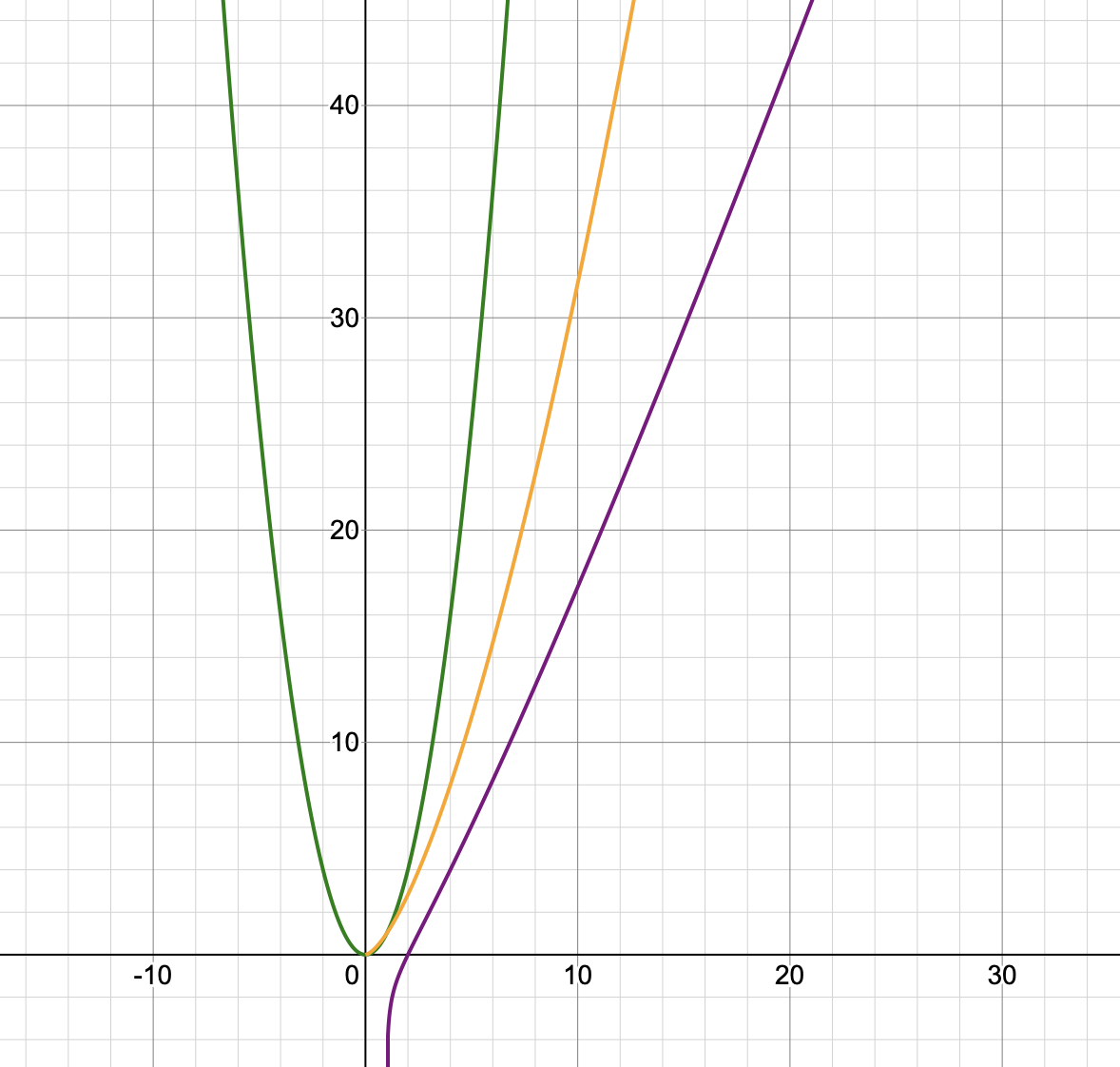
초록색 : 방법 1
노랑색 : 방법 2
보라색 : 방법 3
그럼 실제로도 그런지 위에서 짠 코드를 활용하여 테스트를 해보자.
각각 1만, 5만, 10만, 50만, 100만, 500만, 1000만의 케이스가 주어지고 해당 케이스 수 이하의 모든 소수를 구할 때, 시간이 얼마나 걸리는지 한 번 테스트를 해보자.
코드는 아래와 같이 했으니 참고바란다.
// 소수만 출력
import java.util.ArrayList;
public class Prime_1 {
public static ArrayList<Integer> list;
public static ArrayList<Integer> list2;
public static ArrayList<Integer> list3;
public static void main(String[] args) {
int N = 10000;
for (int i = 0; i < 5; i++) {
System.out.println("Prime Numbers less than or equal to " + N);
list = new ArrayList<Integer>(); // list 초기화
make_prime(N);
list.clear(); // 리스트 비우기
list2 = new ArrayList<Integer>(); // list 초기화
make_prime2(N);
list2.clear(); // 리스트 비우기
list3 = new ArrayList<Integer>(); // list 초기화
make_prime3(N);
list3.clear(); // 리스트 비우기
System.out.println();
if(i % 2 == 0) {
N *= 5;
}
else {
N *= 2;
}
}
}
// 방법 1 : N 이하의 모든 소수
public static long make_prime(int number) {
final long start = System.nanoTime();
boolean TrueFalse; // true : 소수 , false : 비소수
for (int i = 3; i <= number; i++) { // 2는 소수이므로 3 부터 시작
// 0 과 1 은 소수가 아니므로 skip
TrueFalse = true;
for (int j = 2; j < number; j++) {
// 소수가 아닐경우 종료
if (i % j == 0) {
TrueFalse = false;
break;
}
}
// 위 반복문에서 약수를 갖고 있지 않는경우 소수다.
if (TrueFalse)
list.add(i);
}
final long end = System.nanoTime();
System.out.println("run1 : " + (end - start) * 1e-9 + " sec");
return end - start;
}
// 방법 2 : N 이하의 모든 소수
public static long make_prime2(int number) {
final long start = System.nanoTime();
boolean TrueFalse; // true : 소수 , false : 비소수
for (int i = 3; i <= number; i++) { // 2는 소수이므로 3 부터 시작
// 0 과 1 은 소수가 아니므로 skip
TrueFalse = true;
for (int j = 2; j <= Math.sqrt(number); j++) {
// 소수가 아닐경우 종료
if (i % j == 0) {
TrueFalse = false;
break;
}
}
// 위 반복문에서 약수를 갖고 있지 않는경우 소수다.
if (TrueFalse)
list2.add(i);
}
final long end = System.nanoTime();
System.out.println("run2 : " + (end - start) * 1e-9 + " sec");
return end - start;
}
// 방법 3 : N 이하의 모든 소수
public static long make_prime3(int number) {
final long start = System.nanoTime();
boolean[] check = new boolean[number + 1]; // true : 비소수 , false : 소수
check[0] = check[1] = true;
for (int i = 2; i <= Math.sqrt(number); i++) { //
// 0 과 1 은 소수가 아니므로 skip
if (check[i])
continue; // 소수가 아닐경우 skip
for (int j = i * i; j < check.length; j += i) {
check[j] = true;
}
}
for (int i = 0; i < check.length; i++) {
if (!check[i]) list3.add(i); // 소수(flase)인 경우 list3 에 추가
}
final long end = System.nanoTime();
System.out.println("run3 : " + (end - start) * 1e-9 + " sec");
return end - start;
}
}
한 번 기회가 된다면 직접 코드를 돌려보는 것을 추천드린다.
결과는 다음과 같다.

확연히 보기에도 에라토스테네스의 체가 압도적으로 빠르다는 것을 볼 수 있다.
실제로도 1억 이하의 모든 소수를 구하더라도 불과 몇 초 안걸린다.

- 정리
오늘은 소수에 대해 약간의 지식과
소수 판별법, 소수 구하는 방법을 알아보았다.
결과만 말하자면 대부분의 소수 문제는 에라토스테네스의 체를 쓰면 거의 대부분이 풀린다.
알고리즘도 복잡하지 않으면서 매우 좋은 성능을 보여주기 때문이다.
'알고리즘 > Java' 카테고리의 다른 글
| 자바 [JAVA] - 셸 정렬 (Shell Sort) (18) | 2021.02.18 |
|---|---|
| 자바 [JAVA] - 거품 정렬 (Bubble Sort) (2) | 2021.01.18 |
| 자바 [JAVA] - 삽입 정렬 (Insertion Sort) (8) | 2020.11.30 |
| 자바 [JAVA] - 선택 정렬 (Selection Sort) (10) | 2020.11.14 |
| 자바 [JAVA] - 카운팅 정렬 (Counting Sort / 계수 정렬) (36) | 2020.05.29 |