자바 [JAVA] - 셸 정렬 (Shell Sort)
[정렬 알고리즘 모음]
- Shell Sort [셸 정렬]
셸 정렬은 기본적으로 삽입 정렬을 기반으로 하기 때문에 만약 삽입 정렬을 모르신다면 이 글을 읽기 전에 '삽입 정렬'을 보고 오시는 것을 추천드린다.
바로 위에서 말했듯 셸 정렬은 삽입 정렬을 기반으로 한다고 했다.
삽입 정렬이 무엇인가? 삽입 정렬은 현재 비교하고자 하는 target(타겟)과 그 이전의 원소들과 비교하며 자리를 교환(swap)하는 정렬 방법이다.
필자가 링크로 올린 삽입 정렬을 보고 오면 알겠지만, 기본적으로 삽입 정렬은 target(타겟) 원소와 이전 원소들을 비교하여 타겟 원소가 들어갈 위치를 잡는 것이라 만약에 오름차순 기준으로 이전 원소들 보다 target 원소가 작을 경우 이전의 원소들을 모두 탐색하면서 위치를 교환(swap) 해야하는 단점이 존재한다.
그렇다보니 정렬하고자 하는 순서와 반대, 즉 역순에 가까울수록 최악의 시간복잡도를 보이게 된다.
반대로 삽입정렬의 장점은 무엇인가? 거의 정렬 된 상태에 가까울 수록 시간복잡도가 O(N)에 가까워진다.
즉, 장점은 살리면서 단점을 최소화하기 위해 고안 된 방식이 바로 셸 정렬이다.
그렇다면 셸 정렬은 무엇일까?
Shell Sort는 Donald Shell 에 의해 고안된 정렬 방법으로 Shell 이라는 이름이 붙었다.
앞서 설명했듯 Insertion Sort(삽입 정렬)의 장점은 살리면서 단점은 줄인 방식이라고 했다. 일단 단점에 대해 생각해보자. 어떻게 해야 삽입 정렬의 단점을 최소화 시킬 수 있을까?
삽입 정렬의 단점은 오름차순 기준으로 타겟 원소가 이전의 원소보다 작을경우 이전 원소들 모두 교환(swap)을 한다는 것이다. 그럼 이 과정을 줄인다면 어떨까?
즉, 이전의 원소를 모두 비교, 교환하는 것이 아니라 일정 간격 주기로 띄엄띄엄 검사하면서 교환하여 타겟 원소의 위치를 대략적으로 잡아주는 것이다.
그리고 위와 같은 과정을 '간격을 줄여가면서' 정렬해나가다보면 정렬기준에 가까워지지 않겠는가? 그러면 삽입정렬의 장점인 거의 정렬 된 상태일 경우 정렬 속도가 빠르다는 이점 또한 가져갈 수 있다.
쉽게말해 정렬하고자 하는 원소가 10개가 있을 때 간격을 3으로 설정하여 간격이 3인 원소들끼리 삽입정렬을 하고 그 다음 간격을 2로 조정하여 2칸씩 떨어진 원소들끼리 삽입정렬을 하고, 최종적으로 간격이 1인 즉, 우리가 알고있는 기본적인 삽입정렬을 하는 것이다. 이러한 과정을 거치는 것이 바로 셸 정렬이라는 것이다.
셸 정렬은 삽입 정렬을 기반으로 하니 일단 셸 정렬의 특징만 짚고 넘어가보자.
셸 정렬은 데이터를 '비교'하면서 찾기 때문에 '비교 정렬'이며 정렬의 대상이 되는 데이터 외에 추가적인 공간을 필요로 하지 않기 때문에 '제자리 정렬(in-place sort)'이기도 하다. 정확히는 데이터를 서로 교환하는 과정(swap)에서 임시 변수를 필요로 하나, 이는 충분히 무시할 만큼 적은 양이기 때문에 제자리 정렬로 보는 것이다. 이는 선택정렬, 거품 정렬과도 같은 부분이다.
다만, 삽입정렬과는 다르게 일정 간격을 주기로 하여 비교 및 교환이 일어나기 때문에 구조상 안정정렬(Stable Sort)은 아니다.
- 정렬 방법
셸 정렬의 전체적인 과정은 이렇다. (오름차순을 기준으로 설명)
1. 간격(gap)을 설정한다.
2. 각 간격별로 분류 된 서브(부분) 리스트에 대해 삽입정렬을 한다.
3. 각 서브(부분) 리스트의 정렬이 끝나면 간격을 줄인다.
4. 간격이 1이 될 때 까지 2번 과정으로 되돌아가며 반복한다.
이쯤에서 여러분들이 궁금할만 한 점이 하나 생길 것이다.
"그럼 간격은 어떻게 설정해요?"
이 질문에 대한 답은 "정답은 없습니다" 이다.. 왜냐하면 간격(gap)이 너무 적으면 건너 뛰는 간격이 적다는 것, 즉 pass 속도가 느려지고, 반대로 간격이 너무 많으면 오버헤드가 발생하기 때문이다.
그래서 많은 사람들이 각 간격에 따라 평균적으로 좋은 간격들을 내놓았는데, 이를 갭 시퀀스(Gap Sequences)라고 한다.
아래 글을 보면 많은 갭 시퀀스들이 있다는 것을 볼 수 있다.
en.wikipedia.org/wiki/Shellsort#Gap_sequences
Shellsort - Wikipedia
From Wikipedia, the free encyclopedia Jump to navigation Jump to search Sorting algorithm which uses multiple comparison intervals Swapping pairs of items in successive steps of Shellsort with gaps 5, 3, 1 Shellsort, also known as Shell sort or Shell's met
en.wikipedia.org
사진으로 보자면 이렇다.
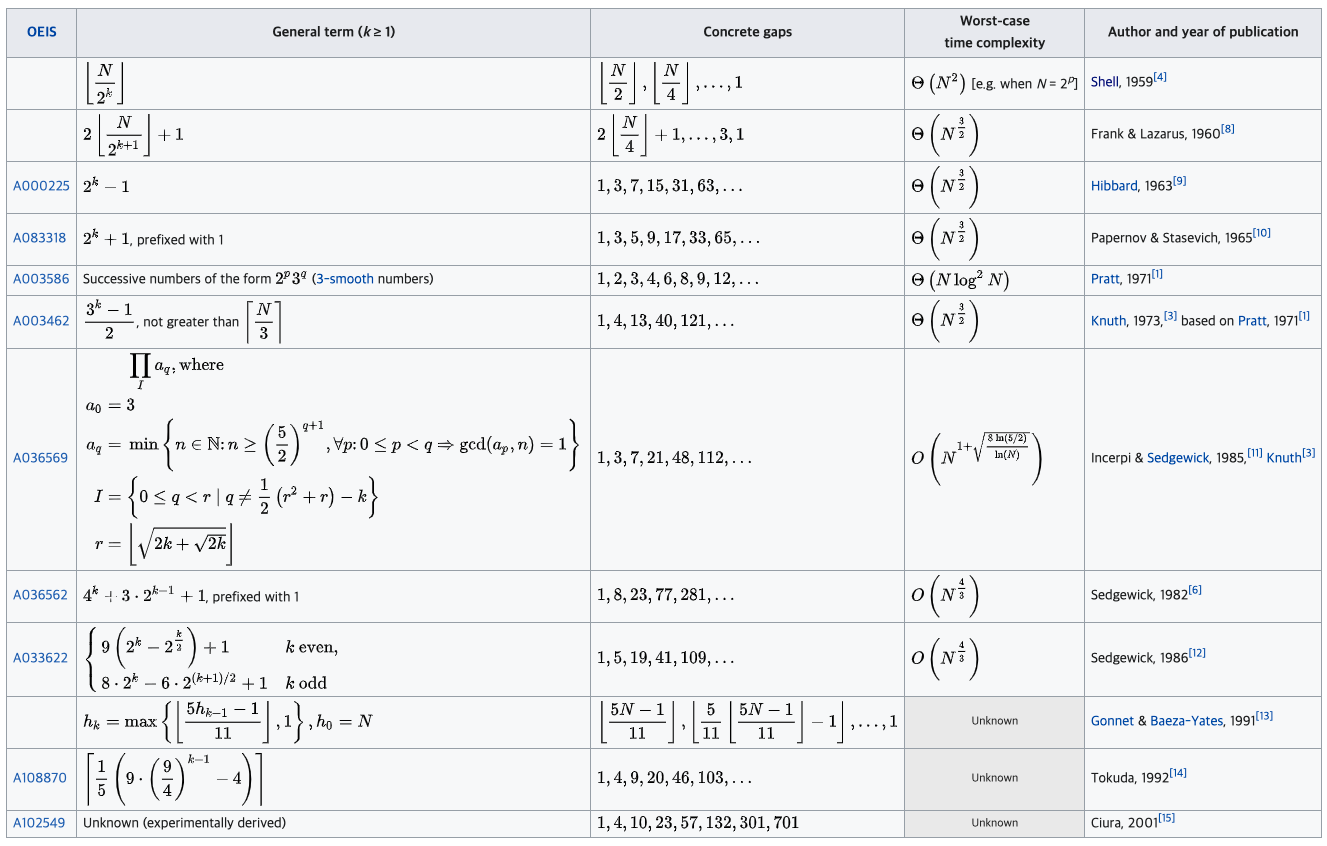
이렇게 많은 gap sequence 들이 있지만, 그래도 가장 대표적으로 많이 다루는 것은 3가지 정도가 된다.
A003462(Knuth Sequence)
A108870(Tokuda Sequence)
A102549(Ciura Sequence)
이 중 우리가 오늘 사용 할 것은 가장 아래에 있는 Ciura 시퀀스를 사용할 것이다. 이유는 다른 건 없고 현재까지 알려진 gap sequence들 중 가장 좋은 퍼포먼스를 보였다고 한다.
다만 문제는 해당 gap sequence는 경험에 의존하여 최선의 시퀀스를 만든 것이기 때문에 현재 알려진 것은 {1, 4, 10, 23, 57, 132, 301, 701, 1750} 까지다.
(1750은 2011년에 추가된 것 같다. 자세한 건 아래 링크에 있다.)
A102549 - OEIS
%I %S 1,4,10,23,57,132,301,701,1750 %N Optimal (best known) sequence of increments for shell sort algorithm. %C Values were found empirically. Better than A033622, A036562, A036564, A036569, and A055875. %D Marcin Ciura, Best Increments for the Average Cas
oeis.org
그럼 리스트가 더 클 경우는 어떻게 해야할까... 이 부분은 앞서 링크한 위키피디아 글의 각 gap sequence를 비교한 표 바로 밑에 쓰여 있다. 아래 글의 빨간색 선으로 마킹한 부분을 읽으면 이렇다.

위 빨간색 줄에서 마지막에 701 이 후 확장된 시퀀스는 결정된게 없다고 보고 있는데, 현재는 1750까지 나왔으니 1750을 기준으로 하여 이 후 gap sequence는 2.25씩 곱하여 gap sequence를 확장 할 수 있다고 하니 그렇게 하여 다음과 같은 갭 시퀀스를 쓰려고 한다.
{ 1, 4, 10, 23, 57, 132, 301, 701, 1750, 3937,
8858, 19930, 44842, 100894, 227011, 510774,
1149241, 2585792, 5818032, 13090572, 29453787,
66271020, 149109795, 335497038, 754868335, 1698453753};(자바의 배열은 Integer.MAX_VALUE(약 21억)을 넘지 못하므로 1698453753까지만 고려하여 gap sequence를 만들면 된다.)
그럼 이제 본격적으로 정렬 과정을 보자.

위와 같이 일정 간격의 원소들끼리 삽입정렬을 시도하면서 그 간격을 점차 줄여나아가면 된다.
얼핏 보기에는 반복을 여러번 하기 때문에 오히려 삽입 정렬보다 성능이 떨어져 보이지만 위 예시를 잘 보면 그렇지 않다. 예로들어 round1의 두 번째 서브리스트인 9와 2를 보자. 만약에 gap 없이, 그러니까 그냥 삽입정렬을 하면 원래의 경우 2는 이전 원소들보다 작기 때문에 총 5번의 비교, 교환 과정이 발생한다.
하지만, 위 처럼 gap을 두고 부분적으로 삽입정렬을 시행하기 때문에 2의 경우 단 한 회만에 gap의 크기인 4만큼 jump(pass) 하여 위치를 잡는다.
이렇게 일정 간격만큼 패스하면서 '거의 정렬 된 상태'로 만들고 최종적으로 마지막에 gap이 1인 삽입정렬을 시도하면 성능이 기존의 삽입 정렬보다 우수해지는 원리인 것이다.
전체적인 흐름을 보자면 다음과 같은 형태로 정렬 한다.

그 외에도 많은 참고 영상들이 있는데, 영상으로 보는 것이 더 쉬울 것 같아 같이 첨부하도록 하겠다.
- Shell Sort 구현하기
public class Shell_Sort {
private final static int[] gap =
{ 1, 4, 10, 23, 57, 132, 301, 701, 1750, 3937,
8858, 19930, 44842, 100894, 227011, 510774,
1149241, 2585792, 5818032, 13090572, 29453787,
66271020, 149109795, 335497038, 754868335, 1698453753}; // 갭을 담고있는 배열
public static void shell_sort(int[] a) {
shell_sort(a, a.length);
}
// 맨 처음 gap을 참조 할 인덱스를 구하는 메소드
private static int getGap(int length) {
int index = 0;
// 최소한 부분 배열의 원소가 2개씩은 비교 되도록 나눠준다.
int len = (int)(length / 2.25);
while (gap[index] < len) {
index++;
}
return index;
}
private static void shell_sort(int[] a, int size) {
int index = getGap(size); // 첫 gap을 사용할 index
// gap[index] 값부터 gap[0] 까지 반복한다.
for (int i = index; i >= 0; i--) {
for (int j = 0; j < gap[i]; j++) { // 각 부분 리스트에 대해 삽입정렬을 한다.
insertion_sort(a, j, size, gap[i]);
}
}
}
/**
*
* @param a 배열
* @param start 부분 배열의 첫 번째 원소 인덱스
* @param size 배열의 전체 크기
* @param gap 현재 gap
*/
private static void insertion_sort(int[] a, int start, int size, int gap) {
// 부분 배열의 두 번째 원소부터 size까지 반복한다. (gap 값씩 건너띔)
for (int i = start + gap; i < size; i += gap) {
int target = a[i];
int j = i - gap;
// 타겟 원소가 이전의 원소보다 작을 때 까지 반복
while (j >= start && target < a[j]) {
a[j + gap] = a[j]; // 이전 원소를 한 칸씩 뒤로 미룬다.
j -= gap;
}
/*
* 위 반복문에서 탈출 하는 경우 앞의 원소가 타겟보다 작다는 의미이므로
* 타겟 원소는 j번째 원소 뒤에 와야한다.
* 그러므로 타겟은 j + gap 에 위치하게 된다.
*/
a[j + gap] = target;
}
}
}
일단, 이해하기 쉽게 삽입정렬을 따로 분리하여 정렬되는 과정을 봤다. 위의 정렬 과정을 이해한다면 다음과 같이 다듬어 좀 더 보기 좋게 만들면서 최적화를 할 수 있다.
public class Shell_Sort {
private final static int[] gap =
{ 1, 4, 10, 23, 57, 132, 301, 701, 1750, 3937,
8858, 19930, 44842, 100894, 227011, 510774,
1149241, 2585792, 5818032, 13090572, 29453787,
66271020, 149109795, 335497038, 754868335, 1698453753}; // 갭을 담고있는 배열
public static void shell_sort(int[] a) {
shell_sort(a, a.length);
}
// 맨 처음 gap을 참조 할 인덱스를 구하는 메소드
private static int getGap(int length) {
int index = 0;
// 최소한 부분 배열의 원소가 2개씩은 비교 되도록 나눠준다.
int len = (int)(length / 2.25);
while (gap[index] < len) {
index++;
}
return index;
}
private static void shell_sort(int[] a, int size) {
int gapIndex = getGap(size);
// 갭이 1이 될 때까지 반복
while(gapIndex >= 0) {
int step = gap[gapIndex--]; // 현재 gap(step)
/*
* --- 삽입 정렬 과정 ---
*
* 각 부분리스트의 두 번째 원소의 인덱스 부터 순회한다.
* 예로들어 step이 3일 때 arr[0], arr[1], arr[2] 는
* 이전 원소와 비교할 것이 없다.
* 그러므로 step부터 순회한다.
*/
for(int i = step; i < size; i++) {
/*
* j는 target 원소가 되며 현재 원소(target) a[j]가 이전 원소 a[j - step]보다
* 작을 때 까지 반복한다.
*/
for (int j = i; j >= step && a[j] < a[j - step]; j -= step) {
/*
* 현재(target) 원소의 인덱스(j)와 이전의 원소(j-step)의 인덱스에 있는
* 원소의 값을 교환한다.
*/
swap(a, j, j - step);
}
}
}
}
private static void swap(int[] a, int i, int j) {
int swap = a[i];
a[i] = a[j];
a[j] = swap;
}
}
이렇게도 구현 할 수 있다.
첫 번째와 조금 순회 방식은 다른데, 첫 번째 방식은 부분 리스트에 대해 하나의 부분리스트를 삽입정렬을 통해 정렬을 완성하고 다음 부분리스트로 넘어간다면, 두 번째 방식은 하나의 부분리스트를 먼저 완료하는 것이 아니라 부분리스트를 한 번씩 돌아가면서 이전 원소들에 대해 삽입정렬을 수행하는 것이다.
- 셸 정렬의 장점 및 단점
[장점]
1. 멀리 있는 원소들끼리 빠르게 비교 및 교환이 이루어진다.
2. 삽입정렬(Insertion Sort), 거품정렬(Bubble Sort)에 비해 정렬 속도가 빠르다.
[단점]
1. 일반적인 삽입정렬에 비해 구현이 까다롭다.
2. gap sequence에 영향을 많이 받으며 적절한 시퀀스를 선택해야 한다.
3. 일정 간격을 두고 원소의 교환이 이루어지기 때문에 안정정렬이 아니다.
시간 복잡도에 대해 잠깐 언급하자면 가장 간단하게 답을 내릴 수 있다. "갭 시퀀스에 따라 달라진다."
왜냐하면, 결국 서브 리스트를 어떻게 분할해서 삽입정렬을 하느냐인데 간단히 구해지는 갭 시퀀스는 어떻게든 시간 복잡도를 구할 수 있다만, 오늘처럼 일정한 규칙이 아닌 경험적으로 얻어낸 시퀀스나 복잡한 수식에 의해 얻어낸 시퀀스의 경우 그 분석이 매우 어렵다.
다만, 이상적으로 최상의 경우나 최악의 경우는 구할 수 있다.
최상의 경우는 이미 정렬 된 상태이면서, gap sequence가 현재 리스트의 크기를 2n 으로 나눌 수 있을 때다. 그러면 삽입정렬 과정에서 이전의 데이터를 한 번만 비교 한 뒤 더이상 비교하지 않기 때문에 사실상 리스트의 원소를 탐색하는 과정이 시간복잡도가 된다.
쉽게 생각해보면 리스트의 크기가 N일 때 이분탐색처럼 N/2 + N/4 + N/8 + ⋯ + 1 이다.
그러면 연산횟수가 x라고 할 때 N이 1일 경우 1에서 2를 x번 곱해야 한다. 즉, N = 1 × 2x 방정식이 나오고, x를 구하기 위해 양변에 로그를 취해 log2N = xlog22 를 만들어 다시 풀면 logN = x 가 된다.
여기서 위 logN 는 특정 값에 다다르기 위한 x이고, 이 과정을 정렬에서는 모든 원소가 한 번씩 해야하기 때문에 logN 이 N번 반복되므로 시간 복잡도는 O(NlogN) 이 된다는 정도다.
최악의 경우는 gap이 1이고 삽입정렬의 가장 단점이였던 '역순으로 된 리스트' 일 경우이므로. 한 마디로 그냥 삽입 정렬과 똑같으면서 최악의 경우를 생각하면 된다. 당연 O(N2)의 시간 복잡도를 갖는다.
하지만 gap을 1로 사용하면 삽입정렬과 다를게 없기 때문에 일반적인 gap sequence에서는 이 또한 얘기가 달라진다.
정리하자면 일반적으로 시간복잡도는 구하기 매우 까다롭고 어려우며 갭 시퀀스에 따라 의존적이다.
이미 초반에 첨부를 했지만, 위키피디아에서는 최악의 경우에 대한 표가 있기 때문에 한 번 더 보여주겠다.

- 정리
셸 정렬의 경우 삽입 정렬의 확장판이라고 생각하면 된다. Shell Sort자체가 안정정렬은 아니지만, 충분히 빠른 정렬이기도 하기 때문에 안정정렬이 필요 없는 primitive type의 경우에는 shell sort로 써도 원소가 무작위인 상황에서는 충분히 쓸만하다고 본다.
각 정렬 알고리즘 별 시간 복잡도와 평균 정렬 속도는 다음과 같다.

보면 삽입 정렬의 정렬의 장점을 이용하여 구현되었기 때문에 매우 좋은 성능을 보이고 있다는 것을 볼 수 있다.
테스트는 필자가 깃허브에 올린 코드를 활용하면 된다.
이번 셸 정렬의 경우 아마 구현 자체는 삽입 정렬의 연장선이라서 그리 어렵지 않게 구현 할 수 있어 쉽게 이해했을 것이다.
혹여 부족한 부분이 있거나 궁금한 점, 모르거나 이해가 가지 않는 부분이 있다면 언제든 댓글 달아주시면 감사하겠다.
그 외에 필자가 여러 타입들에 대해 구현 한 정렬 알고리즘 소스 코드들을 자세히 보고싶다면 아래 깃허브 repo에 업로드되어있으니 이를 참고하시길 바란다.
https://github.com/kdgyun/Sorting_Algorithm.git
kdgyun/Sorting_Algorithm
Contribute to kdgyun/Sorting_Algorithm development by creating an account on GitHub.
github.com
'알고리즘 > Java' 카테고리의 다른 글
| 자바 [JAVA] - 합병정렬 / 병합정렬 (Merge Sort) (24) | 2021.03.31 |
|---|---|
| 자바 [JAVA] - 힙 정렬 (Heap Sort) (31) | 2021.03.14 |
| 자바 [JAVA] - 거품 정렬 (Bubble Sort) (2) | 2021.01.18 |
| 자바 [JAVA] - 삽입 정렬 (Insertion Sort) (8) | 2020.11.30 |
| 자바 [JAVA] - 선택 정렬 (Selection Sort) (10) | 2020.11.14 |