자바 [JAVA] - 삽입 정렬 (Insertion Sort)

 

[정렬 알고리즘 모음]

 

 

1. 계수 정렬 (Counting Sort)

2. 선택 정렬 (Selection Sort)

3. 삽입 정렬 (Insertion Sort) - [현재 페이지]

4. 거품 정렬 (Bubble Sort)

5. 셸 정렬 (Shell Sort)

6. 힙 정렬 (Heap Sort)

7. 합병(병합) 정렬 (Merge sort)

8. 퀵 정렬 (Quick Sort)

9. 이진 삽입 정렬 (Binary Insertion Sort)

10. 팀 정렬 (Tim Sort)

 

 

 

 

 

 

 

 

• Insertion Sort [삽입 정렬]

 

 

 

삽입 정렬은 현재 비교하고자 하는 target(타겟)과 그 이전의 원소들과 비교하며 자리를 교환(swap)하는 정렬 방법이다.

 

말로만 설명하기에는 어려울 수 있으나 그림으로 보면 이해하기 쉬우니 일단 삽입 정렬에 대한 특징만 짚고 넘어가보자.

 

삽입 정렬은 데이터를 '비교'하면서 찾기 때문에 '비교 정렬'이며 정렬의 대상이 되는 데이터 외에 추가적인 공간을 필요로 하지 않기 때문에 '제자리 정렬(in-place sort)'이기도 하다. 정확히는 데이터를 서로 교환하는 과정(swap)에서 임시 변수를 필요로 하나, 이는 충분히 무시할 만큼 적은 양이기 때문에 제자리 정렬로 보는 것이다. 이는 선택정렬과도 같은 부분이다.

 

그리고 이전에 다뤘던 선택 정렬과는 달리 삽입 정렬은 '안정 정렬'이다.

 

 

 

 

 

 

 

 

 

---

• 정렬 방법

 

 

 

 

 

삽입 정렬의 경우 원리 자체는 간단하다. 앞에서부터 해당 원소가 위치 할 곳을 탐색하고 해당 위치에 삽입하는 것이다.

 

 

삽입 정렬의 전체적인 과정은 이렇다. (오름차순을 기준으로 설명)

 

1. 현재 타겟이 되는 숫자와 이전 위치에 있는 원소들을 비교한다. (첫 번째 타겟은 두 번째 원소부터 시작한다.)

2. 타겟이 되는 숫자가 이전 위치에 있던 원소보다 작다면 위치를 서로 교환한다.

3. 그 다음 타겟을 찾아 위와 같은 방법으로 반복한다. 

 

 

즉, 그림으로 보면 다음과 같은 과정을 거친다.

 

 

 

 

 

 

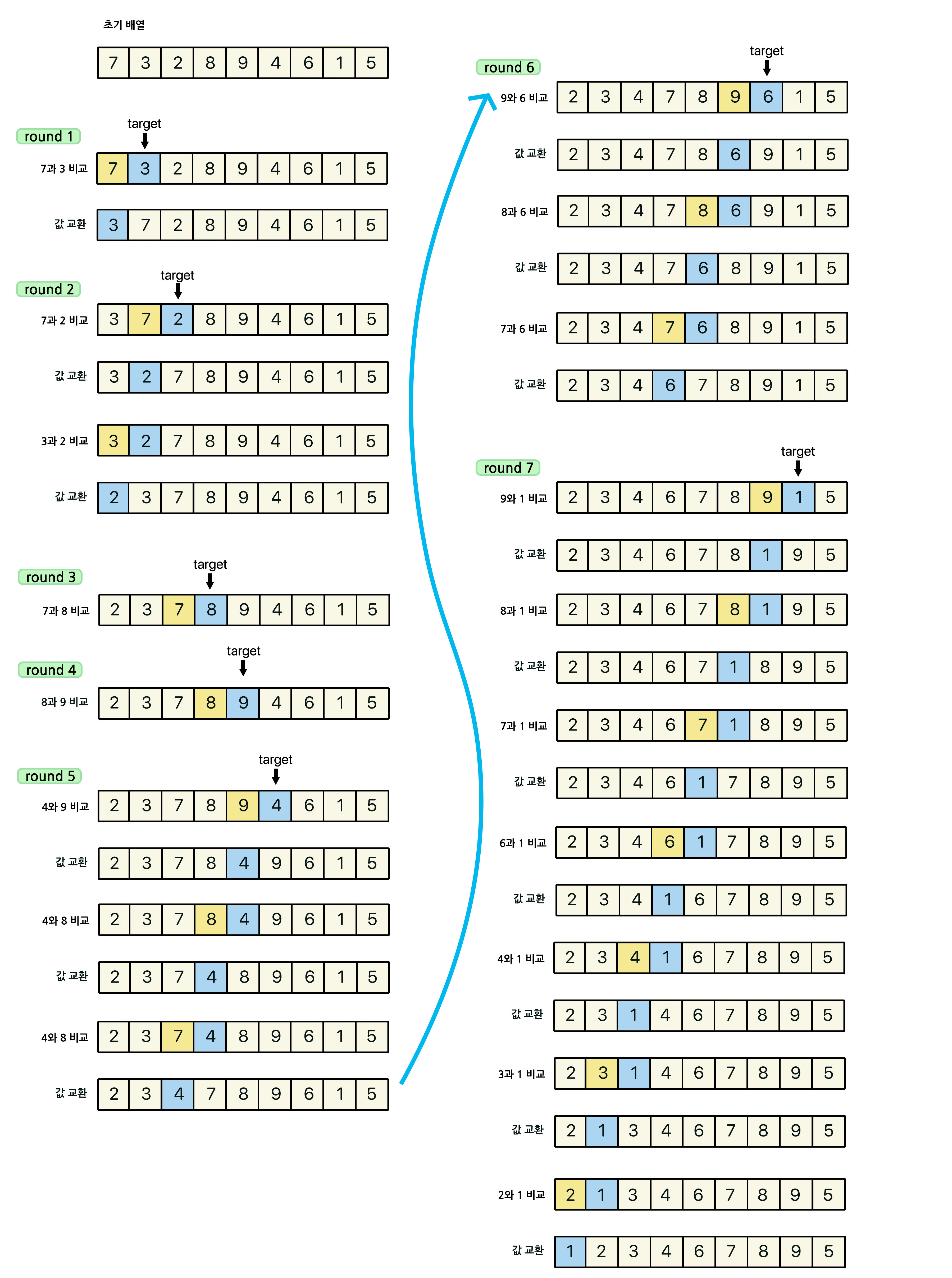
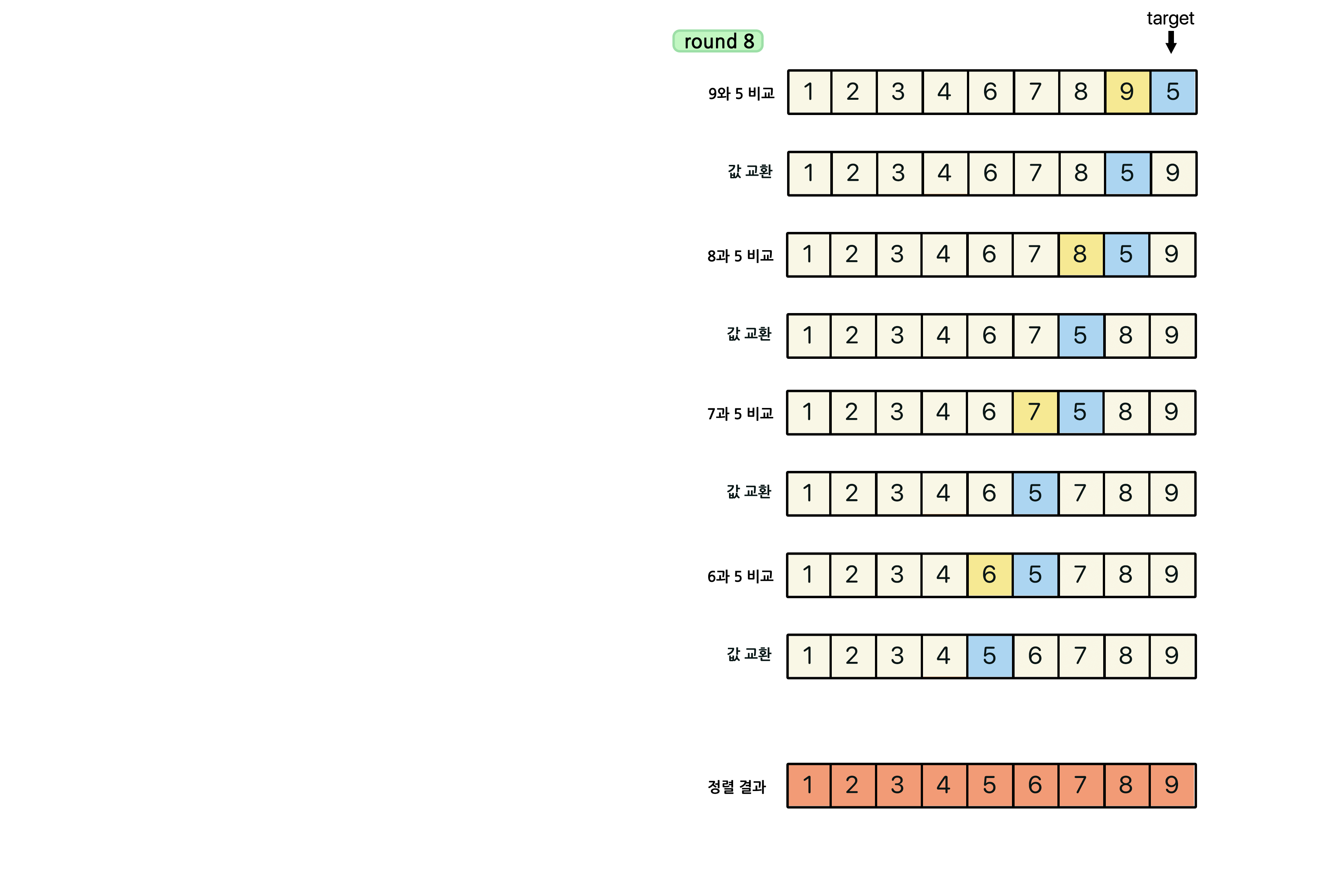
첫 번째 원소는 타겟이 되어도 비교 할 원소가 없기 때문에 처음 원소부터 타겟이 될 필요가 없고 두 번째 원소부터 타겟이 되면 된다.

 

 

 

전체적인 흐름을 보자면 다음과 같은 형태로 정렬 한다.

 

https://en.wikipedia.org/wiki/Insertion_sort

 

 

https://ko.wikipedia.org/wiki/삽입_정렬

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

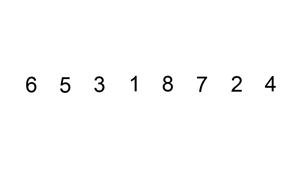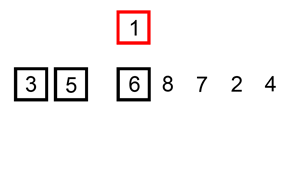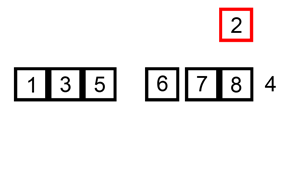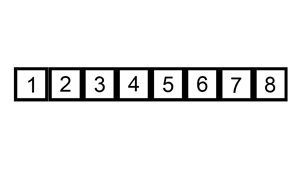
그 외에도 많은 참고 영상들이 있는데, 영상으로 보는 것이 더 쉬울 것 같아 같이 첨부하도록 하겠다.

 

 

 

https://www.youtube.com/watch?v=8oJS1BMKE64&list=PLZh3kxyHrVp_AcOanN_jpuQbcMVdXbqei

 

 

 

 

 

 

---

• Insertion Sort 구현하기

 

 

 

public class Insertion_Sort {

	public static void insertion_sort(int[] a) {
		insertion_sort(a, a.length);
	}
	
	private static void insertion_sort(int[] a, int size) {
		
		
		for(int i = 1; i < size; i++) {
			// 타겟 넘버
			int target = a[i];
			
			int j = i - 1;
			
			// 타겟이 이전 원소보다 크기 전 까지 반복
			while(j >= 0 && target < a[j]) {
				a[j + 1] = a[j];	// 이전 원소를 한 칸씩 뒤로 미룬다.
				j--;
			}
			
			/*
			 * 위 반복문에서 탈출 하는 경우 앞의 원소가 타겟보다 작다는 의미이므로
			 * 타겟 원소는 j번째 원소 뒤에 와야한다.
			 * 그러므로 타겟은 j + 1 에 위치하게 된다.
			 */
			a[j + 1] = target;	
		}
		
	}
}

 

 

 

구현 자체는 어렵지 않다.

 

결과적으로 타겟 이전 원소가 타겟 숫자보다 크기 직전까지 모든 수를 뒤로 한 칸씩 밀어내는 것이다. 

 

 

 

 

 

 

---

 

• 삽입 정렬의 장점 및 단점

[장점]

1. 추가적인 메모리 소비가 작다.

2. 거의 정렬 된 경우 매우 효율적이다. 즉, 최선의 경우 O(N)의 시간복잡도를 갖는다.

3. 안장정렬이 가능하다.

 

 

[단점]

1. 역순에 가까울 수록 매우 비효율적이다. 즉, 최악의 경우 O(N²)의 시간 복잡도를 갖는다.

2. 데이터의 상태에 따라서 성능 편차가 매우 크다. 

 

 

 

 

 

시간복잡도에 대해 잠깐 언급하자면, 위 알고리즘에서도 볼 수 있듯, 타겟 숫자가 이전 숫자보다 크기 전까지 반복하기 때문에 이미 정렬이 되어있는 경우 항상 타겟숫자가 이전 숫자보다 크다. 즉, 값을 N번만 비교하기 때문에 최선의 경우 O(N)의 시간 복잡도를 갖게 되는 것이다.

 

반대로 최악의 경우는 타겟 숫자가 이전 숫자보다 항상 작기 때문에 결국 N 번째 숫자에 대하여 N-1 번을 비교해야 한다. 그렇기 때문에 최악의 경우는 O(N²)의 시간복잡도를 보인다.

 

그럼 평균 시간 복잡도는? 이라는 질문이라면 삽입 정렬의 평균 시간 복잡도 또한 O(N²)의 시간 복잡도를 갖는다.

 

공식을 유도해보자면 이렇다. 

이미 최선의 경우는 O(N)인 것을 알았으니 최악의 경우를 보자.

 

N이 정렬해야하는 리스트의 자료 수, i가 타겟이 되는 인덱스라고 할 때 loop(반복문)을 생각해보자.

 

i=2  일 때, 데이터 비교 횟수는 2-1 = 1번

i=3 일 때, 데이터 비교 횟수는 3-1 = 2번

i=4 일 때, 데이터 비교 횟수는 4-1 = 3 번

                   ⋮

i=N 일 때, 데이터 비교 횟수는 N-1 번

 

즉, 다음과 같이 공식화 할 수 있다.

그리고 N에 대하여 다음을 만족하기 때문에 시간복잡도 또한 도출 할 수 있다.

 

 

자, 그럼 최악과 최선의 경우를 합쳐서 2로 나누면 평균이지 않겠는가? 결과적으로 시간복잡도는 상한선을 의미하기 때문에 아래와 같은 결과를 도출할 수 있다.

 

 

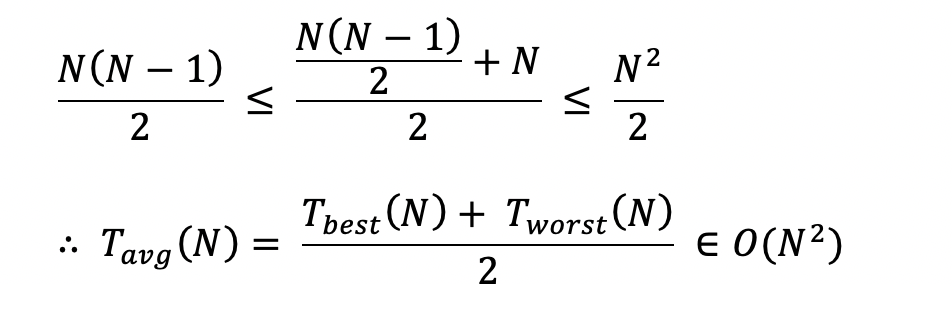
결과적으로 최상의 경우와 최악의 경우의 평균으로 보더라도 '상한선'이라는 개념에 의해 O(N²)이 정설로 보고 있다.

 

 

물론 다음에 다룰 Bubble Sort나 Selection Sort 와 이론상 같은 시간복잡도를 갖음에도 평균 비교 횟수에 대한 기대값이 상대적으로 적기 때문에 평균 시간복잡도가 O(N²) 인 정렬 알고리즘 중에서는 빠른편에 속하는 알고리즘이다.

 

 

 

 

 

 

 

 

 

 

 

---

 

• 정리

 

삽입 정렬의 경우 거의 정렬 된 배열에서 좋은 성능을 보이기 때문에 실제로 병합정렬과 삽입 정렬을 혼합한 Tim Sort(팀 정렬)이 있다. 또한 이 팀 정렬이 프로그래밍 언어에서도 자체 라이브러리로 정렬 알고리즘에 적용하고 있는 언어들이 있다.

 

이후 Tim Sort를 배울 때 삽입 정렬도 다루게 되니 잘 기억해두시길 바란다. (정확히는 이진 삽입 정렬이기 때문에 이후에 이에 대해 다루기 때문에 적어도 삽입 정렬에 대한 메커니즘은 확실하게 이해하고 있어야한다.)

 

그리고 삽입 정렬을 변형하여 만들어낸 Shell Sort(셸 정렬)도 있으니 미리 알아두시길 바란다.

 

이전에 다뤘던 정렬 알고리즘과 앞으로 다룰 정렬 알고리즘들의 정렬 별 성능표는 아래와 같다.. 우리가 구현한 알고리즘은 Insertion Sort이다. 참고로 15만 개의 랜덤 정수를 정렬했으며 총 100번을 반복한 결과를 차트로 제작하였다. 

 

필자가 테스트 한 결과로 Insertion sort는 2초대에 자리하고 있다. (컴퓨터의 환경 및 벤치마크 방식에 따라 달라질 수 있다) 

 

 

 

 

또한 각 정렬 알고리즘 별 시간 복잡도와 평균 정렬 속도는 다음과 같다.

 

 

이후에 차근차근 구현해보겠지만, 각 알고리즘마다 최상과 평균 시간복잡도와 안정성은 어느정도 알고있는 것이 좋다. 

(참고로 Shell Sort의 경우 /가 나눗셈을 의미하는게 아니라 갭 시퀀스(gap sequence)에 따라 시간복잡도가 달라진다. 그래서 'gap sequence가 좋은 경우' / 'gap sequence가 나쁜 경우' 이렇게 보면 된다. 자세한 내용은 shell sort를 다룰 때 말해드리겠다.)

 

 

 

 

 

 

 

이번 삽입 정렬은 매우 기초적인 정렬 방법 중 하나다. 이후 필자가 목표했던 Tim Sort와 Dual-pivot Quick Sort을 다루기 전에 기본 정렬 방식을 확실히 알고 가야 이해할 수 있기 때문에 쉬운 정렬부터 차근차근 올릴 것이다. (그리고 이 번 정렬 방식은 앞으로 구현 할 Tim Sort에서 활용되는 이진 삽입 정렬에 대한 개념에서 또 나오니 잘 기억해두길 바란다.)

 

혹여 부족한 부분이 있거나 궁금한 점, 모르거나 이해가 가지 않는 부분이 있다면 언제든 댓글 달아주시면 감사하겠다.

 

 

그 외에 필자가 여러 타입들에 대해 구현 한 정렬 알고리즘 소스 코드들을 자세히 보고싶다면 아래 깃허브 repo에 업로드되어있으니 이를 참고하시길 바란다.

 

 

https://github.com/kdgyun/Sorting_Algorithm.git

kdgyun/Sorting_Algorithm