자바 [JAVA] - 퀵 정렬 (Quick Sort)
[정렬 알고리즘 모음]
- Quick Sort [퀵 정렬]
이 번에 다뤄볼 정렬은 퀵 정렬이다. 이름에서도 보이듯이 빠른(Quick) 정렬이다.
아마 다른 블로거 혹은 책에서 본 적이 있다면 느끼실 수 있겠지만, 퀵 정렬의 경우 그 구현방법이 정말 다양하다. 그 이유는 조금 뒤에 얘기해보도록 하겠다.
퀵 정렬의 메커니즘은 크게 다음과 같다.
하나의 리스트를 피벗(pivot)을 기준으로 두 개의 부분리스트로 나누어 하나는 피벗보다 작은 값들의 부분리스트, 다른 하나는 피벗보다 큰 값들의 부분리스트로 정렬한 다음, 각 부분리스트에 대해 다시 위 처럼 재귀적으로 수행하여 정렬하는 방법이다.
이 부분에서 만약 알고리즘에 대해 잘 알고있다면 '분할 정복(Divide and Conquer)'을 떠올릴 것이다.
맞다. 퀵 정렬은 기본적으로 '분할 정복' 알고리즘을 기반으로 정렬되는 방식이다. 다만, 병합정렬(Merge Sort)과 다른 점은 병합정렬의 경우 하나의 리스트를 '절반'으로 나누어 분할 정복을 하고, 퀵 정렬(Quick Sort)의 경우 피벗(pivot)의 값에 따라 피벗보다 작은 값을 갖는 부분리스트와 피벗보다 큰 값을 갖는 부분리스트의 크기가 다를 수 있기 때문에 하나의 리스트에 대해 비균등하게 나뉜다는 점이 있다.
실제로도 정렬 방법에서 병합 정렬과 퀵 정렬은 많이 비교되곤 한다. (다만 일반적으로 병합정렬보다 퀵정렬이 빠르다.)
위 말만 들으면 잘 감이 안오실 것 같다.
구체적으로 알아보기에 앞서 미리 언급하자면 퀵 정렬은 데이터를 '비교'하면서 찾기 때문에 '비교 정렬'이며 정렬의 대상이 되는 데이터 외에 추가적인 공간을 필요로 하지 않는다. 그러므로 '제자리 정렬(in-place sort)이다.'
퀵 정렬은 병합정렬과는 다르게 하나의 피벗을 두고 두 개의 부분리스트를 만들 때 서로 떨어진 원소끼리 교환이 일어나기 때문에 불안정정렬(Unstable Sort) 알고리즘이기도 하다.
위 말만 듣는다면 이해하기는 어려울 테니 정렬 방법에 대해 구체적으로 알아보도록 하자.
- 정렬 방법
퀵 정렬의 전체적인 과정은 이렇다.
1. 피벗을 하나 선택한다.
2. 피벗을 기준으로 양쪽에서 피벗보다 큰 값, 혹은 작은 값을 찾는다. 왼쪽에서부터는 피벗보다 큰 값을 찾고, 오른쪽에서부터는 피벗보다 작은 값을 찾는다.
3. 양 방향에서 찾은 두 원소를 교환한다.
4. 왼쪽에서 탐색하는 위치와 오른쪽에서 탐색하는 위치가 엇갈리지 않을 때 까지 2번으로 돌아가 위 과정을 반복한다.
5. 엇갈린 기점을 기준으로 두 개의 부분리스트로 나누어 1번으로 돌아가 해당 부분리스트의 길이가 1이 아닐 때 까지 1번 과정을 반복한다. (Divide : 분할)
6. 인접한 부분리스트끼리 합친다. (Conqure : 정복)
위 6가지 과정에 의해 정렬되는 방식이다.
2~3번 과정의 경우 좀 더 구체적으로 말하자면 대부분의 구현은 현재 리스트의 양 끝에서 시작하여 왼쪽에서는 피벗보다 큰 값을 찾고, 오른쪽에서는 피벗보다 작은 값을 찾아 두 원소를 교환하는 방식이다. 그래야 피벗보다 작은 값은 왼쪽 부분에, 피벗보다 큰 값들은 오른쪽 부분에 치우치게 만들 수 있기 때문이다. 이를 흔히 호어(Hoare)방식이라고 한다.
피벗을 선택하는 과정은 여러 방법이 있는데, 대표적으로 세 가지가 있다.
현재 부분배열의 가장 왼쪽 원소가 피벗이 되는 방법, 중간 원소가 피벗이 되는 방법, 마지막 원소가 피벗이 되는 방법이다.
각각의 방식은 다음과 같다.
(길이가 너무 길어지기 때문에 더 보기로 해두겠다.)
[왼쪽 피벗 선택 방식]
[오른쪽 피벗 선택 방식]
[중간 피벗 선택 방식]
위 3 가지 방식 모두 특징은 '피벗'을 하나 설정하고 피벗보다 작은 값들은 왼쪽에, 큰 값들은 오른쪽에 치중하도록 하는 것이다. 이 과정을 흔히 파티셔닝(Partitioning)이라고 한다.
그렇게 파티셔닝을 했다면 파티셔닝을 통해 배치 된 피벗의 위치를 기준으로 좌우 부분리스트로 나누어 각각의 리스트에 대해 재귀호출을 해주면 된다.
위 원리를 이해해야 앞으로 구현 할 dual-pivot quick sort(이중 피벗 퀵 정렬) 또한 이해하기가 쉬울 것이다.
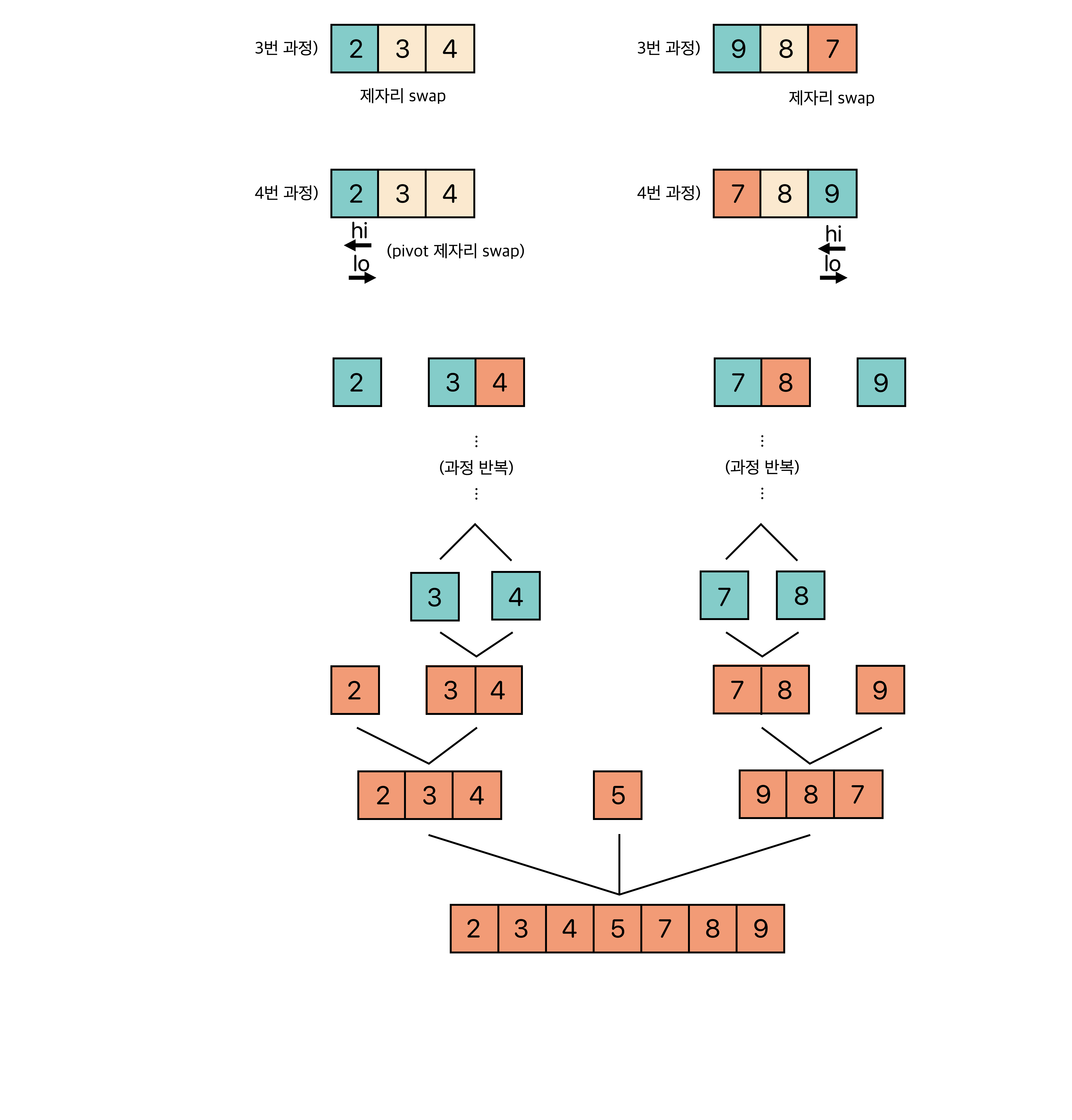
그리고 혹시 몰라 움직이는 이미지로 이해할 수 있도록 이미지를 첨부했다.
전체적인 흐름을 보자면 다음과 같은 형태로 정렬 한다.

그 외에도 많은 참고 영상들이 있는데, 영상으로 보는 것이 더 쉬울 것 같아 같이 첨부하도록 하겠다.
(위 영상은 중간 요소를 피벗으로 설정하여 정렬하는 과정이다)
- Quick Sort 구현하기
그러면 일단 구현을 해야 할 것이다.
퀵 정렬의 경우 결국 피벗을 어느 곳을 기준으로 잡을 것인지가 관건일 것이다. 이러한 부분 때문에, 여러 블로거 혹은 책들마다 구현 방식이 매우 상이하다는 것이다.
일단 가장 기본적인 퀵 정렬을 구현해보도록 하겠다. 이해하기 가장 쉬우면서 기본적인 방법은 왼쪽 피벗 선택 방식이다. 위에서 설명한 방식을 그대로 구현하면 된다. (자세한 건 주석과 함께 달아놓겠다.)
[왼쪽 피벗 선택 방식]
public class QuickSort {
public static void sort(int[] a) {
l_pivot_sort(a, 0, a.length - 1);
}
/**
* 왼쪽 피벗 선택 방식
* @param a 정렬할 배열
* @param lo 현재 부분배열의 왼쪽
* @param hi 현재 부분배열의 오른쪽
*/
private static void l_pivot_sort(int[] a, int lo, int hi) {
/*
* lo가 hi보다 크거나 같다면 정렬 할 원소가
* 1개 이하이므로 정렬하지 않고 return한다.
*/
if(lo >= hi) {
return;
}
/*
* 피벗을 기준으로 요소들이 왼쪽과 오른쪽으로 약하게 정렬 된 상태로
* 만들어 준 뒤, 최종적으로 pivot의 위치를 얻는다.
*
* 그리고나서 해당 피벗을 기준으로 왼쪽 부분리스트와 오른쪽 부분리스트로 나누어
* 분할 정복을 해준다.
*
* [과정]
*
* Partitioning:
*
* a[left] left part right part
* +---------------------------------------------------------+
* | pivot | element <= pivot | element > pivot |
* +---------------------------------------------------------+
*
*
* result After Partitioning:
*
* left part a[lo] right part
* +---------------------------------------------------------+
* | element <= pivot | pivot | element > pivot |
* +---------------------------------------------------------+
*
*
* result : pivot = lo
*
*
* Recursion:
*
* l_pivot_sort(a, lo, pivot - 1) l_pivot_sort(a, pivot + 1, hi)
*
* left part right part
* +-----------------------+ +-----------------------+
* | element <= pivot | pivot | element > pivot |
* +-----------------------+ +-----------------------+
* lo pivot - 1 pivot + 1 hi
*
*/
int pivot = partition(a, lo, hi);
l_pivot_sort(a, lo, pivot - 1);
l_pivot_sort(a, pivot + 1, hi);
}
/**
* pivot을 기준으로 파티션을 나누기 위한 약한 정렬 메소드
*
* @param a 정렬 할 배열
* @param left 현재 배열의 가장 왼쪽 부분
* @param right 현재 배열의 가장 오른쪽 부분
* @return 최종적으로 위치한 피벗의 위치(lo)를 반환
*/
private static int partition(int[] a, int left, int right) {
int lo = left;
int hi = right;
int pivot = a[left]; // 부분리스트의 왼쪽 요소를 피벗으로 설정
// lo가 hi보다 작을 때 까지만 반복한다.
while(lo < hi) {
/*
* hi가 lo보다 크면서, hi의 요소가 pivot보다 작거나 같은 원소를
* 찾을 떄 까지 hi를 감소시킨다.
*/
while(a[hi] > pivot && lo < hi) {
hi--;
}
/*
* hi가 lo보다 크면서, lo의 요소가 pivot보다 큰 원소를
* 찾을 떄 까지 lo를 증가시킨다.
*/
while(a[lo] <= pivot && lo < hi) {
lo++;
}
// 교환 될 두 요소를 찾았으면 두 요소를 바꾼다.
swap(a, lo, hi);
}
/*
* 마지막으로 맨 처음 pivot으로 설정했던 위치(a[left])의 원소와
* lo가 가리키는 원소를 바꾼다.
*/
swap(a, left, lo);
// 두 요소가 교환되었다면 피벗이었던 요소는 lo에 위치하므로 lo를 반환한다.
return lo;
}
private static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
위와 같이 왼쪽 피벗을 선택해서 피벗보다 작은 요소들은 왼쪽에, 피벗보다 큰 요소들은 오른쪽에 치중시킨 뒤, 피벗의 위치를 최종적으로 들어갈 위치와 교환해준 뒤 그 위치를 반환하는 메소드가 partition메소드고, 반환 된 피벗의 위치를 기준으로 왼쪽과 오른쪽 부분리스트로 나누어 재귀적으로 분할정복을 해주는 것이다.
오른쪽 피벗 선택 방식 또한 위 방식에서 역순으로만 해주면 된다. (자세한 건 주석과 함께 달아놓겠다.)
[오른쪽 피벗 선택 방식]
public class QuickSort {
public static void sort(int[] a) {
r_pivot_sort(a, 0, a.length - 1);
}
/**
* 오른쪽 피벗 선택 방식
* @param a 정렬할 배열
* @param lo 현재 부분배열의 왼쪽
* @param hi 현재 부분배열의 오른쪽
*/
private static void r_pivot_sort(int[] a, int lo, int hi) {
/*
* lo가 hi보다 크거나 같다면 정렬 할 원소가
* 1개 이하이므로 정렬하지 않고 return한다.
*/
if(lo >= hi) {
return;
}
/*
* 피벗을 기준으로 요소들이 왼쪽과 오른쪽으로 약하게 정렬 된 상태로
* 만들어 준 뒤, 최종적으로 pivot의 위치를 얻는다.
*
* 그리고나서 해당 피벗을 기준으로 왼쪽 부분리스트와 오른쪽 부분리스트로 나누어
* 분할 정복을 해준다.
*
* [과정]
*
* Partitioning:
*
* left part right part a[right]
* +---------------------------------------------------------+
* | element < pivot | element >= pivot | pivot |
* +---------------------------------------------------------+
*
*
* result After Partitioning:
*
* left part a[hi] right part
* +---------------------------------------------------------+
* | element < pivot | pivot | element >= pivot |
* +---------------------------------------------------------+
*
*
* result : pivot = hi
*
*
* Recursion:
*
* r_pivot_sort(a, lo, pivot - 1) r_pivot_sort(a, pivot + 1, hi)
*
* left part right part
* +-----------------------+ +-----------------------+
* | element <= pivot | pivot | element > pivot |
* +-----------------------+ +-----------------------+
* lo pivot - 1 pivot + 1 hi
*
*/
int pivot = partition(a, lo, hi);
r_pivot_sort(a, lo, pivot - 1);
r_pivot_sort(a, pivot + 1, hi);
}
/**
* pivot을 기준으로 파티션을 나누기 위한 약한 정렬 메소드
*
* @param a 정렬 할 배열
* @param left 현재 배열의 가장 왼쪽 부분
* @param right 현재 배열의 가장 오른쪽 부분
* @return 최종적으로 위치한 피벗의 위치(lo)를 반환
*/
private static int partition(int[] a, int left, int right) {
int lo = left;
int hi = right;
int pivot = a[right]; // 부분리스트의 오른쪽 요소를 피벗으로 설정
// lo가 hi보다 작을 때 까지만 반복한다.
while(lo < hi) {
/*
* hi가 lo보다 크면서, lo의 요소가 pivot보다 큰 원소를
* 찾을 떄 까지 lo를 증가시킨다.
*/
while(a[lo] < pivot && lo < hi) {
lo++;
}
/*
* hi가 lo보다 크면서, hi의 요소가 pivot보다 작거나 같은 원소를
* 찾을 떄 까지 hi를 감소시킨다.
*/
while(a[hi] >= pivot && lo < hi) {
hi--;
}
// 교환 될 두 요소를 찾았으면 두 요소를 바꾼다.
swap(a, lo, hi);
}
/*
* 마지막으로 맨 처음 pivot으로 설정했던 위치(a[right])의 원소와
* hi가 가리키는 원소를 바꾼다.
*/
swap(a, right, hi);
// 두 요소가 교환되었다면 피벗이었던 요소는 hi에 위치하므로 hi를 반환한다.
return hi;
}
private static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
오른쪽 피벗 선택 방식도 그렇게 어려운 것은 없을 것이다. 왼쪽 피벗 선택 방식에서 순서와 부등호만 약간 수정해주면 된다.
마지막으로 중간 피벗 선택 방식인데, 이 부분은 약간 고려해야 할 것들이 있다. 일단 코드를 보면서 확인해보자.
[중간 피벗 선택 방식]
public class QuickSort {
public static void sort(int[] a) {
m_pivot_sort(a, 0, a.length - 1);
}
/**
* 중간 피벗 선택 방식
* @param a 정렬할 배열
* @param lo 현재 부분배열의 왼쪽
* @param hi 현재 부분배열의 오른쪽
*/
private static void m_pivot_sort(int[] a, int lo, int hi) {
/*
* lo가 hi보다 크거나 같다면 정렬 할 원소가
* 1개 이하이므로 정렬하지 않고 return한다.
*/
if(lo >= hi) {
return;
}
/*
* 피벗을 기준으로 요소들이 왼쪽과 오른쪽으로 약하게 정렬 된 상태로
* 만들어 준 뒤, 최종적으로 pivot의 위치를 얻는다.
*
* 그리고나서 해당 피벗을 기준으로 왼쪽 부분리스트와 오른쪽 부분리스트로 나누어
* 분할 정복을 해준다.
*
* [과정]
*
* Partitioning:
*
* left part a[(right + left)/2] right part
* +---------------------------------------------------------+
* | element < pivot | pivot | element >= pivot |
* +---------------------------------------------------------+
*
*
* result After Partitioning:
*
* left part a[hi] right part
* +---------------------------------------------------------+
* | element < pivot | pivot | element >= pivot |
* +---------------------------------------------------------+
*
*
* result : pivot = hi
*
*
* Recursion:
*
* m_pivot_sort(a, lo, pivot) m_pivot_sort(a, pivot + 1, hi)
*
* left part right part
* +-----------------------+ +-----------------------+
* | element <= pivot | | element > pivot |
* +-----------------------+ +-----------------------+
* lo pivot pivot + 1 hi
*
*/
int pivot = partition(a, lo, hi);
m_pivot_sort(a, lo, pivot);
m_pivot_sort(a, pivot + 1, hi);
}
/**
* pivot을 기준으로 파티션을 나누기 위한 약한 정렬 메소드
*
* @param a 정렬 할 배열
* @param left 현재 배열의 가장 왼쪽 부분
* @param right 현재 배열의 가장 오른쪽 부분
* @return 최종적으로 위치한 피벗의 위치(hi)를 반환
*/
private static int partition(int[] a, int left, int right) {
// lo와 hi는 각각 배열의 끝에서 1 벗어난 위치부터 시작한다.
int lo = left - 1;
int hi = right + 1;
int pivot = a[(left + right) / 2]; // 부분리스트의 중간 요소를 피벗으로 설정
while(true) {
/*
* 1 증가시키고 난 뒤의 lo 위치의 요소가 pivot보다 큰 요소를
* 찾을 떄 까지 반복한다.
*/
do {
lo++;
} while(a[lo] < pivot);
/*
* 1 감소시키고 난 뒤의 hi 위치가 lo보다 크거나 같은 위치이면서
* hi위치의 요소가 pivot보다 작은 요소를 찾을 떄 까지 반복한다.
*/
do {
hi--;
} while(a[hi] > pivot && lo <= hi);
/*
* 만약 hi가 lo보다 크지 않다면(엇갈린다면) swap하지 않고 hi를 리턴한다.
*/
if(lo >= hi) {
return hi;
}
// 교환 될 두 요소를 찾았으면 두 요소를 바꾼다.
swap(a, lo, hi);
}
}
private static void swap(int[] a, int i, int j) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
중간 선택 방식은 조금은 복잡하다. 일단 중간 위치를 피벗으로 설정하게 되면 필자가 이미지로 첨부한 것에서도 볼 수 있듯이 hi가 가리키는 위치가 pivot의 위치보다 높으면서 hi가 가리키는 원소가 pivot보다 작은 경우가 생긴다.
그렇기 때문에 분할정복으로 재귀를 호출하더라도 파티셔닝을 통해 얻은 피벗까지 포함하여 부분리스트로 나누어야 한다.
실제로 이 방식은 큰 장점이 있어 위와 같은 방식의 피벗 선택을 많이 추천하곤 한다. 이 부분은 바로 다음 파트에서 설명하도록 하겠다.
- 퀵 정렬의 장점 및 단점
[장점]
1. 특정 상태가 아닌 이상 평균 시간 복잡도는 NlogN이며, 다른 NlogN 알고리즘에 비해 대체적으로 속도가 매우 빠르다. 유사하게 NlogN 정렬 알고리즘 중 분할정복 방식인 merge sort에 비해 2~3배정도 빠르다. (정리 부분의 표 참고)
2. 추가적인 별도의 메모리를 필요로하지 않으며 재귀 호출 스택프레임에 의한 공간복잡도는 logN으로 메모리를 적게 소비한다.
[단점]
1. 특정 조건하에 성능이 급격하게 떨어진다.
2. 재귀를 사용하기 때문에 재귀를 사용하지 못하는 환경일 경우 그 구현이 매우 복잡해진다.
위에서 시간 복잡도에 대해 O(NlogN) 으로 유지가 된다고 했다. 이는 합병(병합)정렬과 같은 이유이기 떄문에 표를 그대로 갖고오겠다.
왜 그러한 시간복잡도가 나오는지 한 번 같이 알아보도록 하자.

이상적으로 피벗이 중앙에 위치되어 리스트를 절반으로 나눈다고 할 때, N개의 데이터가 있는 리스트를 1개까지 쪼개어 트리로 나타내게 되면 이진트리(Binary Tree) 형태로 나온다는 것은 우리가 확인 할 수 있다.
N개 노드에 대한 이진트리의 높이(h)는 logN 인 것은 힙정렬에서 다뤘으므로 해당 링크를 참고하시길 바란다.
그러면 비교 및 정렬 과정을 생각해보아야 한다.
우리가 피벗을 잡고 피벗보다 큰 요소와 작은 요소를 각 끝단에서 시작하여 탐색하며 만족하지 못하는 경우 swap을 한다. 이는 현재 리스트의 요소들을 탐색하기 때문에 O(N)이다.
좀 더 자세하게 말하자면 i번 째 레벨에서 노드의 개수가 2i 개이고, 노드의 크기. 한 노드에 들어있는 원소 개수는 N/2i 개다.
이를 곱하면 한 레벨에서 비교작업에 대한 시간 복잡도는 O(2i × N/2i) 이고 이는 곧 O(N)이다.
그리고 O(N)의 비교작업을 트리의 높이인 logN -1 번 수행하므로 다음과 같이 표기할 수 있다.
O(N) × O(logN)
최종적으로 위를 계산하면 O(NlogN) 의 시간복잡도를 갖는 것을 알 수 있다.
위와 달리 반대로 최악의 경우도 있다. (퀵 정렬의 최대의 단점이다.)
바로 정렬 된 상태의 배열을 정렬하고자 할 때다.
간단한 예시로 왼쪽을 기준으로 피벗을 잡을 때를 생각해보자.
우리가 N개가 있는 리스트에 대해 가장 왼쪽 요소를 pivot을 잡고, pivot보다 작은 요소는 왼쪽에, 큰 요소는 오른쪽에 위치시켜 두 부분리스트로 나누게 된다. 이때 만약 pivot이 가장 작은 요소였다면 부분리스트는 어떻게 나눠질까?
왼쪽의 부분리스트는 없고, N-1개의 요소를 갖는 오른쪽 부분리스트만 생성될 것이다.
이를 반복적으로 재귀호출을 해본다고 해보자.
결과적으로 각 재귀 레벨에서 N개의 비교작업을 N번 재귀호출을 하기 때문에 O(N2) 의 최악의 성능을 내기도 한다.

마찬가지로 정렬할 리스트가 이미 내림차순으로 정렬되어있다면 위 트리에서 왼쪽 서브 트리로 치중되어버릴 것이다. 마찬가지로 O(N2) 의 시간복잡도를 갖게 된다.
이는 왼쪽 피벗을 선택하건, 오른쪽 피벗을 선택하건 위와같이 트리가 치중되는 건 마찬가지다. 이 때문에 만약 위 처럼 치중 될 경우 공간 복잡도 또한 O(N)으로 되어버린다.
그래서 중간 피벗이 선호되는 이유가 바로 이러한 이유 때문이다. 그러면 거의 정렬 된 배열이더라도 거의 중간지점에 가까운 위치에서 왼쪽 리스트와 오른쪽 리스트가 균형에 가까운 트리를 얻어낼 수 있기 때문이다. (물론 아예 불가능한 건 아니다.)
그러면 위와 같이 거의 정렬 된 상태의 배열에서 효과적으로 해결할 수 있다.
그럼 왜 다른 O(NlogN) 정렬 방법들에 비해 빠른가에 대해 궁금할 것이다. 만약 Shell Sort 가 다른 정렬 알고리즘에 비해 빠른편에 속하는 이유를 알고 있다면 좀 더 쉽게 이해 할 것이다.
기본적으로 Shell Sort나, Quick Sort는 정렬 방식이 '멀리 떨어진 요소와 교환'되는 정렬 방식이다. Shell Sort는 일정 간격을 두고 두 원소의 값을 비교하며 정렬하고, Quick Sort 또한 양 끝에서 피벗을 기준으로 피벗보다 작은 값을 갖는 위치에 있어야 할 원소가 피벗보다 크거나, 그 반대인 경우 서로 원소를 교환하는 방식이다.
이러한 방식은 해당 원소가 최종적으로 있어야 할 위치에 거의 근접하게 위치하도록 하기 때문에 효율이 좋은 것이다.
예로들어 9번째 원소가 3번째에 위치해야 한다고 할 때, 보통의 경우 9 → 8 → 7 → 6 → 5 → 4 → 3 이런식으로 자기가 현재 있는 위치와 바로 직전의 원소와 교환되면서 총 6번에 걸쳐 이동을 했었어야 한다면, Shell Sort나 Quick Sort의 경우 9 → 1 -> 4 -> 3 서로 떨어져있는 비연속적 원소가 교환되면서 원래 있어야 할 위치에 거의 근접하게 위치하도록 하기 때문에 빠른 정렬이 가능한 것이다.
대신에 위와 같이 정렬하는 경우 별도의 배열이나 플래그(flag)를 부여하지 않는한 대부분의 정렬의 경우 안정정렬은 안된다고 보면 된다.
- 정리
퀵 정렬의 경우 대부분의 정렬들에 비해 빠른 속도를 자랑하기 때문에 많이 다뤄지는 정렬이다. 또한 자바에서는 primitive 타입 배열들의 경우 앞으로 구현 할 dual-pivot quick sort 을 기본 정렬로 사용하고 있기 때문에 이 정렬의 기본 베이스인 quick sort를 이해하고 넘어가야 dual-pivot quick sort의 내용 또한 어렵지 않게 이해할 수 있을 것이다.
또한 여러분들이 시간이 된다면 위와 같이 거의 정렬 된 상태에서 성능이 매우 떨어진다는 점을 고려 할 때, 임계값을 설정하여 일정 크기 이하로 떨어질 경우 정렬 된 배열에서 좋은 성능을 발휘하는 Insertion sort(삽입 정렬)을 하도록 바꾸면 거의 정렬 된 배열에서도 어느정도 성능 하락을 방지할 수 있으니 이렇게 혼합하여 구현해보는 것도 추천 드린다.
각 정렬 알고리즘 별 시간 복잡도와 평균 정렬 속도는 다음과 같다.

보면 quick sort의 경우 매우 빠른 편인 것을 볼 수 있다. (참고로 중간 피벗 선택 방식이다.)
이번 퀵 정렬의 경우 분할정복 알고리즘을 알고있어야 하기 때문에 만약 이에 대한 기본 지식이 없을 경우 어려울 수 있는 정렬방식이다. 또한 피벗을 어떻게 선택하냐의 문제와 잘못된 참조가 있는지를 고려해야 하기 때문에 이전까지 구현했던 정렬들과 다르게 조금 복잡한 정렬 방법이기도 하다.
혹여 부족한 부분이 있거나 궁금한 점, 모르거나 이해가 가지 않는 부분이 있다면 언제든 댓글 달아주시면 감사하겠다.
그 외에 필자가 여러 타입들에 대해 구현 한 정렬 알고리즘 소스 코드들을 자세히 보고싶다면 아래 깃허브 repo에 업로드되어있으니 이를 참고하시길 바란다.
https://github.com/kdgyun/Sorting_Algorithm.git
kdgyun/Sorting_Algorithm
Contribute to kdgyun/Sorting_Algorithm development by creating an account on GitHub.
github.com
'알고리즘 > Java' 카테고리의 다른 글
| 자바 [JAVA] - 팀 정렬 (Tim Sort) (10) | 2021.11.02 |
|---|---|
| 자바 [JAVA] - 이진 삽입 정렬 (Binary Insertion Sort) (8) | 2021.08.01 |
| 자바 [JAVA] - 합병정렬 / 병합정렬 (Merge Sort) (24) | 2021.03.31 |
| 자바 [JAVA] - 힙 정렬 (Heap Sort) (31) | 2021.03.14 |
| 자바 [JAVA] - 셸 정렬 (Shell Sort) (18) | 2021.02.18 |