[백준] 11653번 : 소인수분해 - JAVA [자바]
11653번: 소인수분해
첫째 줄에 정수 N (1 ≤ N ≤ 10,000,000)이 주어진다.
www.acmicpc.net
-
문제
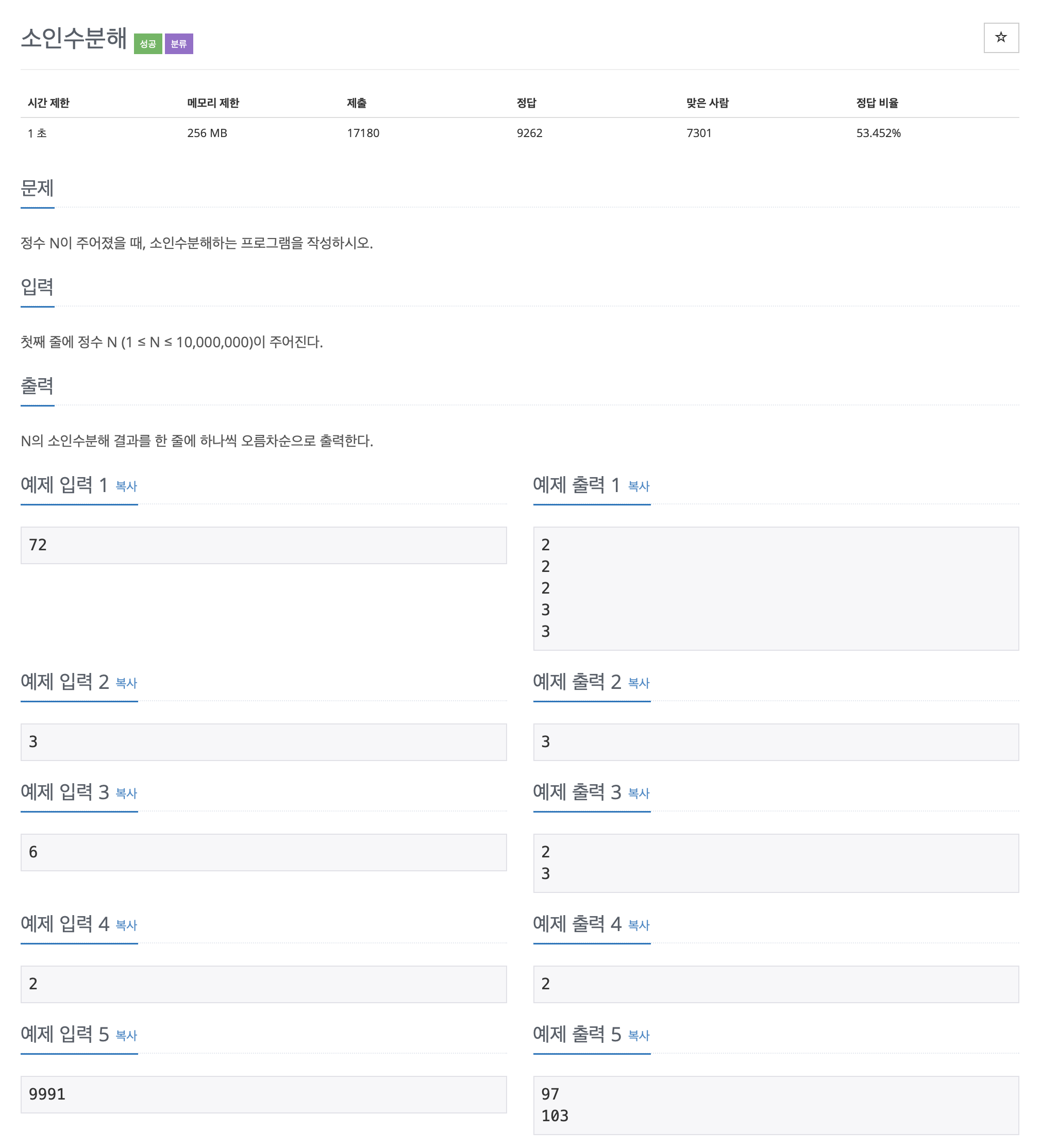
소인수 분해 문제다. 찾아보니 중학교 교과과정에서 배운다고 하니 아마 다들 쉽게 풀 수 있을 듯 하다.
- 알고리즘 [접근 방법]
소인수분해 문제 자체는 어렵지 않으니 잠깐 소인수분해에 대해 알아보면 좋을 것 같다.
소인수분해가 어릴 때 부터 배우면서 약수와 배수를 구하기 위해 쓰이면서 자연스럽게 많이 쓰기 때문에 어떤 것인지는 대강 알고있으나 정확한 정의나 왜 소인수분해인지는 모르고 가는 경우가 많다.
사실 수학용어를 번역하면서 한자 뜻을 빌려와 쓰기 때문에 그렇기도 하다. 오히려 영어 뜻을 그대로 번역하는게 이해하기 쉬울 때도 많다.
그럼 소인수분해를 영어로 어떻게 표현할까?
소인수 분해를 영어로 하면 prime factorization 이라고 한다.
prime 은 소수(1과 자기 자신으로만 나누어 떨어지는 정수)를 의미한다. 그리고 factorization에서 보면 factor + ization이 결합된 문장인 것을 볼 수 있다.
factor는 말그대로 요소, 인수, 인자를 의미하고 -ization은 접미사로 본 형태는 ~ize에서 파생된 것인데, ~ize가 '~화 되다'를 의미한다면 ~ization은 ~ize를 명사화 해서 말 그대로 '~화'를 의미한다. 흔히 붙는다. (예로들어 socialize 는 '사회화 되다'라는 의미, socialization 은 사회화 의미로 된다.) 즉, factorization은 쉽게 말하면 '인수화'라는 의미고 이는 곧 인수분해랑 같은 의미다. 수학적으로 말하면 어떤 수를 인수로 분해하는 것을 의미할 것이다.
그럼 prime과 factorization의 뜻을 합치면 '소수 인수화' 또는 '소수인수분해'라고 하는 겁니다. 다만 번역하면 소수의 '수'와 인수의 '수'가 같은 수로 동어반복이기 때문에 '소인수'라고 합쳐진 것이다.
참고로 한자로 표기하자면 소인수분해는 素因數分解 이고, 소수는 素數 이다.
즉, 소인수분해는 어떤 수를 소수인 인수로 분해하는 것이다.
이 소인수분해가 중요한 이유는 현대 암호학의 가장 기본 토대가 되는 부분이기 때문이다. 앞으로 여러분이 암호학에 관심을 갖게 된다면 배우겠지만, 아직까지 소인수분해를 일률적으로 구할 수 있는 공식을 발견하지 못했기 때문이다.
즉, 두 수의 곱셈을 결과로 나타내기는 쉬워도 결과를 두 수의 곱셈으로 나타내기 어렵다는 역발상에서 시작되는 것이 암호학의 가장 기초다.
혹여 이러한 내용에 관심이 있다면 아래 포스팅을 참고하면 좋을 것 같다.
패스워드의 암호화와 저장 - Hash(해시)와 Salt(솔트)
'암호화는 그 어느 시스템의 정보보다 가장 중요하며 가장 안전해야 하는 것이다' 필자가 "프로그래머로써 가장 중요하게 생각해야 할 것 하나만 뽑는다면?" 이라는 질문이 들어온다면 위와 같��
st-lab.tistory.com
그럼 본격적으로 알고리즘을 파헤쳐보자.
가장 쉬운 방법은 2부터 N까지 모든 수를 나눠보면서 나머지가 0일 경우 그 값을 출력하는 것이다. 즉, 아래와 같이 구할 수 있다. (1의 경우는 소수가 아니므로 당연히 제외되어야 한다.)
for(int i = 2; i <= N; i++) {
while(N % i == 0) {
println(i);
N /= i;
}
}
물론 위와같이 구해도 문제는 없지만 좀 더 효율적으로 짤 수도 있다.
어떤 N이 두 개이상 곱셈(인수)으로 나타낼 수 있을 때 인수 중 한 개 이상은 반드시 √N보다 작거나 같다는 것이다.
즉, 반복문의 범위를 √N까지 반복하는 것이다.
그리고 이 때 중요한 점은, N /= i로 나누고 남은 최종 N이 두 가지 케이스로 나뉜다는 것이다.
예로들어 N = 16이 입력되었다고 가정해보자.
반복문으로 √N까지 한다고 하면 4까지 반복을 할 것이다.
그리고 처음 2에서 while문의 조건식을 만족(16 % 2 == 0)하면서 2를 출력한 다음 N을 2로 나누어 8이 되고, 다시 8 % 2 == 0 을 만족하므로 또다시 2를 출력한 뒤 N을 2로 나누어 4가 되고 이런식으로 쭉 가다가 마지막에 2 % 2 == 0 을 만족하여 2를 다시 한 번 출력한 뒤, N을 2로 나누어 1이 되고 while문 반복을 종료하게 된다. 그리고 1이 인수분해 되는 일은 없으므로 for문 또한 종료가 된다.
반대로 N = 34가 입력되었다고 가정해보자.
반복문으로 √N까지 한다고 하면 근사값이 대략 5.83이므로 5까지 반복을 할 것이다.
그리고 처음 2에서 while문의 조건식 34 % 2 == 0 이므로 2를 출력한 다음 N을 2로 나눌 것이다. 그러면 17이므로 17 % 2 는 0이 아니기 때문에 while문은 종료된다. 그리고 for반복문 i값이 1씩 증가해서 검사하다가 i = 5 가 되면 종료가 되어버린다. 그렇게 되면 N은 17이라는 인수를 갖고 있는데 출력을 못하고 종료가 되어버리는 문제가 생긴다.
즉, for반복문을 종료하고 N이 1이 아니라면 N은 소수이자 인수인 것이 자명하기 때문에 한 번 더 출력해주는 조건문을 달아주어야 한다. 즉 다음과 같이 써야한다.
for(int i = 2; i <= sqrt(N); i++) { // 또는 i * i <= N
while(N % i == 0) {
println(i);
N /= i;
}
}
if(N != 1) {
println(N);
}
이를 토대로 알고리즘을 작성하면 끝난다.
- 3가지 방법을 사용하여 풀이한다.
기본적으로 알고리즘은 √N까지 반복하는 것으로 쓸 것이다. 굳이 N까지 검사해줄 필요가 없기 때문에.. 대신 입력과 출력을 달리하여 성능차이를 볼 것인데, 입력은 Scanner와 BufferedReader을 쓸 것이고 출력은 매 번 출력하는 방식과 StringBuilder을 사용하여 출력하는 방식을 사용해볼 것이다.
다음과 같은 3가지 방식을 이용할 것이니 참고하시길 바란다.
1. Scanner + System.out.println()
2. Scanner + StringBuilder
3. BufferedReader + StringBuilder
- 풀이
- 방법 1 : [Scanner + System.out.println()]
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
for (int i = 2; i <= Math.sqrt(N); i++) { // 또는 i * i <= N
while (N % i == 0) {
System.out.println(i);
N /= i;
}
}
if (N != 1) {
System.out.println(N);
}
}
}
가장 기본적인 방법이라 할 수 있겠다.
- 방법 2 : [Scanner + StringBuilder]
입력 방법을 Scanner 대신 BufferedReader 을 사용하여 풀이하는 방법이다. 단, BufferedReader 는 문자열을 한 줄로 읽기 때문에 N과 M을 구분하기 위해 공백을 기준으로 문자열을 분리해주어야하니 StringTokenizer 을 사용하여 풀도록 하겠다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
StringBuilder sb = new StringBuilder();
int N = in.nextInt();
for (int i = 2; i <= Math.sqrt(N); i++) { // 또는 i * i <= N
while (N % i == 0) {
sb.append(i).append('\n');
N /= i;
}
}
if (N != 1) {
sb.append(N);
}
System.out.println(sb);
}
}
출력을 바꾼 방식이다. BufferedWriter을 써도 되지만, BufferedWriter을 쓸 줄 안다면 대부분 BufferedReader도 쓸테니..
- 방법 3 : [BufferedReader + StringBuilder]
입력 방법을 Scanner 대신 BufferedReader 을 사용하여 풀이하는 방법이다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int N = Integer.parseInt(br.readLine());
for (int i = 2; i <= Math.sqrt(N); i++) {
while (N % i == 0) {
sb.append(i).append('\n');
N /= i;
}
}
if (N != 1) {
sb.append(N);
}
System.out.println(sb);
}
}
- 성능

채점 번호 : 20597227 - 방법 3 : BufferedReader + StringBuilder
채점 번호 : 20597227 - 방법 2 : Scanner + StringBuilder
채점 번호 : 20597227 - 방법 1 : Scanner + System.out.println()
입력의 경우는 확실히 Scanner 보다는 BufferedReader 가 빠른 걸 볼 수 있다. 다만 몇가지 TC를 보니 랜덤데이터인지 체점서버 문제인지는 모르겠지만 매번 출력하는 경우 200ms가 나올 때도 있고 위 처럼 120ms가 나올 때도 있어서 위 이미지에서는 차이가 거의 없는 것으로 나온다.
- 정리
워낙 쉬웠던 문제라 크게 어렵지 않았다. 그래서 소인수에 대해 좀 더 알고갔으면 하는 마음에 소인수분해에 대해 조금 내용보충을 하였다. 혹여 이해가 가지 않는 부분이 있다면 댓글 달아주시면 최대한 빠르게 답변드리도록 하겠다.
'JAVA - 백준 [BAEK JOON] > 기타 문제' 카테고리의 다른 글
| [백준] 17298번 : 오큰수 - JAVA [자바] (45) | 2021.01.21 |
|---|---|
| [백준] 15236번 : Dominos - JAVA [자바] (0) | 2020.11.01 |
| [백준] 1003번 : 피보나치 함수 - JAVA [자바] (24) | 2020.07.22 |
| [백준] 2748번 : 피보나치 수 2 - JAVA [자바] (6) | 2020.07.21 |
| [백준] 1011번 : Fly me to the Alpha Centauri - JAVA [자바] (43) | 2020.04.07 |