[백준] 1003번 : 피보나치 함수 - JAVA [자바]
1003번: 피보나치 함수
각 테스트 케이스마다 0이 출력되는 횟수와 1이 출력되는 횟수를 공백으로 구분해서 출력한다.
www.acmicpc.net
- 문제

이전의 피보나치 수를 풀어보셨다면 쉽게 풀 수 있는 문제다. 이 문제는 피보나치 수를 구할 때, fibonacci(0)과 fibonacci(1)이 각각 몇 번 호출되는지를 묻는 문제다.
- 알고리즘 [접근 방법]
이 문제 또한 풀이방법은 여러가지다.
대표적으로 정석적인 방법인 재귀(Top-Down)를 이용하여 풀이하는 방법이 있고, 다른 하나는 반복문(Bottom-Up)을 사용하여 계산하는 방법이 있다.
혹여 피보나치 수를 DP로 풀이하는 방법을 모르신다면 아래 링크의 포스팅을 한 번 읽어보고 오는 것을 추천한다.
[백준] 2748번 : 피보나치 수 2 - JAVA [자바]
st-lab.tistory.com
DP 재귀 풀이법
위 참고 포스팅을 보셨다면 알겠지만, 재귀호출을 할 때 이미 한 번 탐색(연산)했던 값이 있다면 또다시 연산하는 것이 아니라 이미 계산된 값을 재사용하여 반복적인 연산과정을 줄이는 방법이 DP풀이의 기초다.
이전 글에서는 피보나치 수를 배열에 담아 만약 해당 배열에 값이 없다면 fibonacci(N - 1) + fibonacci(N - 2) 을 통해 재귀호출을 해주었고, 만약 배열에 값이 있다면(이미 이전에 호출했었던 N이라면) 해당 배열값을 바로 반환해주었다.
이번 문제는 그럼 DP로 어떻게 접근해야 할까?
일단, 이번 문제는 피보나치 수를 구하는 것이 아니라 피보나치 수에서 0과 1이 호출되는 횟수를 구하는 것이다.
예로들자면 이런 것이다.
N=2 일 때, Fibonacci(2) = Fibonacci(1) + Fibonacci(0) 이므로 0과 1은 각각 1번씩 호출된다.
N=3 일때는 Fibonacci(3) = Fibonacci(2) + Fibonacci(1) 이고 이는 다시
Fibonacci(3) = (Fibonacci(1) + FibonaccI(0)) + Fibonacci(1) 이므로 0은 1번, 1은 2번 호출된다.
이렇게 N에대하여 각 0과 1이 호출된 횟수를 저장하면 되지 않겠는가?
간단하게 생각해보자. 만약 처음에 N=20 이 입력되어 20에 대해 0과 1 호출횟수를 구한다면 Fibonacci(19) 에 대해서도 자연스럽게 구해질 것이고, Fibonacci(18), Fibonacci(17), ⋯ 해서 N 이하의 모든 수들은 자연스럽게 0과 1을 찾기위해 하위단계로 재귀호출될 것이다.
즉, N=20 에 대해 구한다음에 만약 N=15 같이 이하의 수가 입력된다면 또 다시 재귀호출 할 필요 없이 이미 연산과정에서 한 번 탐색이 이루어졌으므로 바로 해당 값을 꺼내면 된다.
이 과정을 DP로 풀어내면 된다는 의미다. 즉, 한 번 탐색할 때마다 해당 N의 0과 1의 값을 저장해두고, 이후 다음 탐색에서 이미 탐색했던 노드일 경우 해당 배열값을 쓰면 된다.
코드로는 N이 최대 40 까지 주어지고, 각 N에 0과 1이 호출된 횟수를 담아야 하므로 2차원 배열이 있어야겠다. (또한 null 체크를 하기 위해 int[][] 배열이 아닌 Integer[][] 배열로 쓸 것이다. int[][] 배열을 쓰고자 한다면 모든 배열의 값을 -1 과 같은 값으로 모두 초기화 해주길 바란다.)
static Integer[][] dp = new Integer[41][2];
dp[0][0] = 1; // N=0 일 때의 0 호출 횟수
dp[0][1] = 0; // N=0 일 때의 1 호출 횟수
dp[1][0] = 0; // N=1 일 때의 0 호출 횟수
dp[1][1] = 1; // N=1 일 때의 1 호출 횟수
statc Integer[] fibonacci(int N) {
// N에 대한 0, 1의 호출 횟수가 없을 떄(탐색하지 않은 값일 때)
if(dp[N][0] == null || dp[N][1] == null) {
// 각 N에 대한 0 호출 횟수와 1 호출 횟수를 재귀호출한다.
dp[N][0] = fibonacci(N - 1)[0] + fibonacci(N - 2)[0];
dp[N][1] = fibonacci(N - 1)[1] + fibonacci(N - 2)[1];
}
// N에 대한 0과 1, 즉 [N][0]과 [N][1] 을 담고있는 [N]을 반환한다.
return dp[N];
}
위와 같은 알고리즘을 통해 풀어낼 수 있다.
dp 라는 배열을 선언하고, 피보나치 함수는 각 N에 대한 0과 1의 값을 dp에 저장하면서 재귀호출을 해주는 것이다.
이 방법이 문제의 취지에 가장 정석적인(?) 방법이지 않을까 생각된다.
DP 반복문 풀이법
대부분의 알고리즘은 규칙성이 있다는 것, 즉 수식화 할 수 있다. 간단하게 말해서 N=0 부터 시작하여 몇 개를 쭉 나열하다보면 규칙성이 보일 가능성이 높다는 것이다.
한 번 쭉 나열해보자.
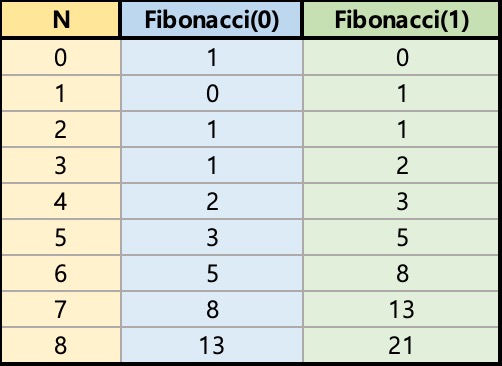
규칙성이 보이는가?
보면 N에 대한 0과 1은 다음과 같은 규칙을 따른다.
1. N에 대한 0호출 횟수 = N-1의 1 호출 횟수
2. N에 대한 1 호출 횟수 = N-1의 0 호출 횟수 + N-1의 1 호출 횟수
위 규칙을 반복문으로 풀자면 다음과 같다.
// 기본 값(N=0일 때)
int zero = 1;
int one = 0;
int zero_plus_one = 1;
for (int i = 0; i < N; i++) {
zero = one; // 0호출 횟수를 이전의 1호출 횟수로 변경
one = zero_plus_one; // 1호출 횟수를 이전의 0과 1호출 횟수의 합으로 변경
zero_plus_one = zero + one; // 0과 1 호출의 합 계산
}
이렇게 하여 N에대한 0과 1 호출 횟수를 쉽게 구할 수 있다.
아마 다들 어렵지 않게 이해했으리라 본다
- 4가지 방법을 사용하여 풀이한다.
이 번에는 입출력과 알고리즘을 달리하여 각 성능별로 비교해보고자 한다.
입력에서는 BufferedReader가 Scanner보다 빠르다는 것은 충분히 이제는 알고있으리라 생각되므로 Scanner에서만 입출력 차이를 두고, BufferedReader을 통해 각 알고리즘별 성능을 비교해 볼 것이다. 즉, 다음과 같이 4가지 풀이방법을 보여주겠다.
1. 재귀 + Scanner + System.out.println 반복출력
2. 재귀 + Scanner + StringBuilder
3. 재귀 + BufferedReader + StringBuilder
4. 반복문 + BufferedReader + StringBuilder
- 풀이
- 방법 1 : [재귀 + Scanner + System.out.println 반복출력]
import java.util.Scanner;
public class Main {
static Integer[][] dp = new Integer[41][2];
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
dp[0][0] = 1; // N=0 일 때의 0 호출 횟수
dp[0][1] = 0; // N=0 일 때의 1 호출 횟수
dp[1][0] = 0; // N=1 일 때의 0 호출 횟수
dp[1][1] = 1; // N=1 일 때의 1 호출 횟수
int T = in.nextInt();
while(T-- > 0){
int N = in.nextInt();
fibonacci(N);
System.out.println(dp[N][0] + " " + dp[N][1]);
}
}
static Integer[] fibonacci(int N) {
// N에 대한 0, 1의 호출 횟수가 없을 떄(탐색하지 않은 값일 때)
if(dp[N][0] == null || dp[N][1] == null) {
// 각 N에 대한 0 호출 횟수와 1 호출 횟수를 재귀호출한다.
dp[N][0] = fibonacci(N - 1)[0] + fibonacci(N - 2)[0];
dp[N][1] = fibonacci(N - 1)[1] + fibonacci(N - 2)[1];
}
// N에 대한 0과 1, 즉 [N][0]과 [N][1] 을 담고있는 [N]을 반환한다.
return dp[N];
}
}
가장 기본적인 방법이라 할 수 있겠다.
참고로 필자는 while문이 쓰기 편해서 위와같이 while(T-->0)이라고 했지만, for문으로 대체해도 무방하다.
- 방법 2 : [재귀 + Scanner + StringBuilder]
출력을 반복적으로 하는대신 StringBuilder을 사용하여 풀이하는 방법이다.
import java.util.Scanner;
public class Main {
static Integer[][] dp = new Integer[41][2];
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
dp[0][0] = 1; // N=0 일 때의 0 호출 횟수
dp[0][1] = 0; // N=0 일 때의 1 호출 횟수
dp[1][0] = 0; // N=1 일 때의 0 호출 횟수
dp[1][1] = 1; // N=1 일 때의 1 호출 횟수
int T = in.nextInt();
StringBuilder sb = new StringBuilder();
while(T-- > 0){
int N = in.nextInt();
fibonacci(N);
sb.append(dp[N][0] + " " + dp[N][1]).append('\n');
}
System.out.print(sb);
}
static Integer[] fibonacci(int N) {
// N에 대한 0, 1의 호출 횟수가 없을 떄(탐색하지 않은 값일 때)
if(dp[N][0] == null || dp[N][1] == null) {
// 각 N에 대한 0 호출 횟수와 1 호출 횟수를 재귀호출한다.
dp[N][0] = fibonacci(N - 1)[0] + fibonacci(N - 2)[0];
dp[N][1] = fibonacci(N - 1)[1] + fibonacci(N - 2)[1];
}
// N에 대한 0과 1, 즉 [N][0]과 [N][1] 을 담고있는 [N]을 반환한다.
return dp[N];
}
}
크게 어려울 것은 없을 것이다. 출력이 얼마나 될지 모르는 문제들은 되도록이면 BufferedWriter나 StringBuilder을 사용하여 풀이하는 것이 성능상으로 이점이 많다.
- 방법 3 : [재귀 + BufferedReader + StringBuilder]
이번에는 BufferedReader 을 사용하여 입력을 받는 방식이다. 알고리즘은 변경되는 것이 없으니 어려운 점은 없을 것이라 본다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
static Integer[][] dp = new Integer[41][2];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
dp[0][0] = 1; // N=0 일 때의 0 호출 횟수
dp[0][1] = 0; // N=0 일 때의 1 호출 횟수
dp[1][0] = 0; // N=1 일 때의 0 호출 횟수
dp[1][1] = 1; // N=1 일 때의 1 호출 횟수
int T = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
while(T --> 0){
int N = Integer.parseInt(br.readLine());
fibonacci(N);
sb.append(dp[N][0] + " " + dp[N][1]).append('\n');
}
System.out.println(sb);
}
static Integer[] fibonacci(int N) {
// N에 대한 0, 1의 호출 횟수가 없을 떄(탐색하지 않은 값일 때)
if(dp[N][0] == null || dp[N][1] == null) {
// 각 N에 대한 0 호출 횟수와 1 호출 횟수를 재귀호출한다.
dp[N][0] = fibonacci(N - 1)[0] + fibonacci(N - 2)[0];
dp[N][1] = fibonacci(N - 1)[1] + fibonacci(N - 2)[1];
}
// N에 대한 0과 1, 즉 [N][0]과 [N][1] 을 담고있는 [N]을 반환한다.
return dp[N];
}
}
위 방법이 가장 기본적인 문제의 취지에 맞게 풀이한 코드가 아닐까 싶다. 또한 이렇게 DP를 잘 활용할 줄 알아야 이후의 그리디 알고리즘에서 좀 더 편하게 풀 수 있을 것이다. 꼭 개념을 잘 이해하도록 하자.
- 방법 4 : [반복문 + BufferedReader + StringBuilder]
이번에는 위 알고리즘 설명에서 보여주었던 반복문으로 푸는 방식이다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
static int zero;
static int one;
static int zero_plus_one;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
for (int i = 0; i < T; i++) {
int N = Integer.parseInt(br.readLine());
fibonacci(N);
sb.append(zero).append(' ').append(one).append('\n');
}
System.out.println(sb);
}
public static void fibonacci(int N) {
// 반드시 초기화 해야한다.
zero = 1;
one = 0;
zero_plus_one = 1;
for (int i = 0; i < N; i++) {
zero = one;
one = zero_plus_one;
zero_plus_one = zero + one;
}
}
}
크게 어려울 것은 없을 것이다. 그리고 정적변수 값만 변경하면 되기 때문에 따로 fibonacci함수에서 return 할 것이 없다. 그렇기 때문에 void로 함수를 구성해주도록 하자.
- 성능

채점 번호 : 21146371 - 방법 4 : 반복문 + BufferedReader + StringBuilder
채점 번호 : 21146367 - 방법 3 : 재귀 + BufferedReader + StringBuilder
채점 번호 : 21146361 - 방법 2 : 재귀 + Scanner + StringBuilder
채점 번호 : 21146357 - 방법 1 : 재귀 + Scanner + System.out.println 반복출력
입력의 경우는 확실히 Scanner 보다는 BufferedReader 가 빠른 걸 볼 수 있다. 그리고 반복문과 재귀로 풀이하는 것에 큰 차이는 없는 것 같다. 수가 그리 크기 않거나 테스트 케이스가 적어서 그런가..
..
- 정리
DP를 이용한 풀이 방법은 꼭 필자의 방법처럼 하지 않아도 된다. 애초에 중복되는 연산과정을 줄이기 위해 고안된 방법론이기 때문에 0과 1을 저장하지 않고 다른 값을 저장할 수도 있다. 그러나 확실한 것은 DP 개념을 정확히 알고있어야 앞으로의 프로그래밍에서 좀 더 효율적으로 데이터를 처리할 수 있다.
DP는 데이터 탐색에 있어 가장 기본중의 기본이 되는 효율적 탐색의 기초라고 필자는 생각한다. 그만큼 여러분들 또한 이에 대한 개념을 정확하게 이해할 수 있었으면 좋겠다.
혹여 어렵거나 모르는 부분이 있으면 댓글 남겨주시면 최대한 빠르게 답변드리도록 하겠다.
'JAVA - 백준 [BAEK JOON] > 기타 문제' 카테고리의 다른 글
| [백준] 15236번 : Dominos - JAVA [자바] (0) | 2020.11.01 |
|---|---|
| [백준] 11653번 : 소인수분해 - JAVA [자바] (3) | 2020.10.18 |
| [백준] 2748번 : 피보나치 수 2 - JAVA [자바] (6) | 2020.07.21 |
| [백준] 1011번 : Fly me to the Alpha Centauri - JAVA [자바] (43) | 2020.04.07 |
| [백준] 10996번 : 별 찍기 - 21 - JAVA [자바] (2) | 2020.03.15 |