자바 [JAVA] - 카운팅 정렬 (Counting Sort / 계수 정렬)
[정렬 알고리즘 모음]
- Counting Sort [계수 정렬 / 카운팅 정렬]
Counting Sort... 계수 정렬, 카운팅 정렬 등으로 많이 불리지만, 가장 와닿는 단어는 카운팅 정렬이므로 이 포스팅에서는 카운팅 정렬로 통일하여 쓰겠다.
카운팅 정렬은 수많은 정렬 알고리즘 중 시간복잡도가 𝚶(𝑛) 으로 엄청난 성능을 보여주는 알고리즘이다. 보통 빠르다는 정렬 알고리즘으로는 대표적으로 퀵 정렬(Quick Sort), 힙 정렬(Heap Sort), 합병 정렬(Merge Sort) 등이 있는데, 이들의 평균 시간복잡도는 𝚶(nlogn) 인 것에 비하면 엄청난 속도인 것은 당연지사다.
기본적으로 정렬이라하면 데이터끼리 직접 비교하는 경우가 많다. 그렇기 때문에 데이터 직접 비교를 사용하는 정렬 알고리즘의 경우 𝚶(nlogn) 보다 작아질 수 없는 것이 한계다. 그렇다면 카운팅 정렬은 어떻게 이를 극복한 것일까?
그럼에도 왜 퀵 정렬같은 𝚶(nlogn) 의 정렬 알고리즘을 많이 사용하는 것일까?
이에 대해 같이 알아보자.
- 정렬 방법
카운팅 정렬의 기본 메커니즘은 아주 단순하다. 데이터의 값이 몇 번 나왔는지를 세주는 것이다. 말 그대로 counting 하는 것이다.
그림으로 차근차근 이해해보자.
먼저 아래와 같은 배열이 있다고 가정해보자.

- 과정 1
array 를 한 번 순회하면서 각 값이 나올 때마다 해당 값을 index 로 하는 새로운 배열(counting)의 값을 1 증가시킨다.
과정으로 보면
array[0] = 7 이므로 counting[7] 값을 1 증가,
array[1] = 2 이므로 counting[2] 값을 1 증가,
...
array[11] = 1 이므로 count[1] 값을 1 증가.
이렇게 과정을 거친다. 이 과정을 마치면 다음 그림처럼 된다.
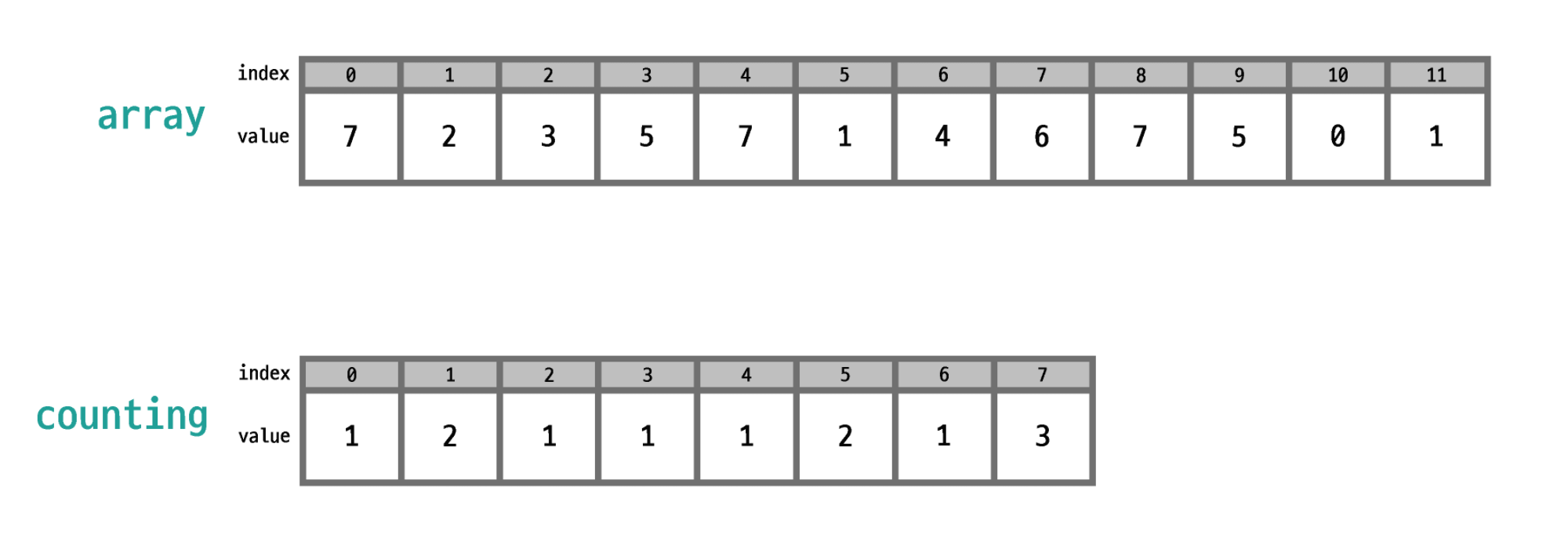
counting 배열의 의미는 다음과 같다.
0의 개수는 1개
1의 개수는 2개
2의 개수는 1개
...
이런식으로 counting 배열은 각 값의 개수가 담겨있는 배열이 된다.
- 과정 2
counting 배열의 각 값을 누적합으로 변환시킨다.
말로는 이해가 어려울 수 있으니, 그림으로 보여주겠다.
이런식으로 counting 배열 값들을 누적합으로 설정해준다.
즉, 우리는 다음과 같은 두 배열을 갖고 있게 되는 것이다.

여기서 우리가 알 수 있는 것은 정렬을 할 경우 counting 배열의 각 값은 (시작점 - 1)을 알려준다는 것이다.
무슨 말인지는 마지막 과정 3을 보면서 이해해보자.
- 과정 3
마지막 단계다.
앞서 잠깐 언급했듯이, counting 배열의 각 값은 (시작점 - 1)을 알려준다고 했다. 즉, 해당 값에 대응되는 위치에 배정하면 된다는 의미다. 간단하게 예를 들면 이렇게 되는 것이다.
array[0] = 7 이고, counting[7] = 12 이다. 여기서 countin[7] 의 값에 1 을 빼준 뒤 해당 값이 새로운 배열의 인덱스 11에 위치하게 된다.
array[1] = 2 이고, counting[2] = 4 이다. 여기서 countin[2] 의 값에 1 을 빼준 뒤 해당 값이 새로운 배열의 인덱스 3에 위치하게 된다.
이런식으로 쭉 하면 된다.
다만 안정적으로 정렬하기 위해서는 array의 마지막 index 부터 순회하는 것이 좋다.
그림으로 보자면 다음과 같다.

이런식으로 하면 result 배열은 array 배열의 정렬된 형태로 있게 된다.
이 과정 자체가 두 수를 비교하는 과정이 없기 때문에 빠른 배치가 가능하다. 다만 보다시피 몇가지 단점 또한 존재한다.
바로 counting 배열이라는 새로운 배열을 선언해주어야 한다는 점이다. 생각보다 이 단점이 꽤 클 수 있는데, array 안에 있는 max값의 범위에 따라 counting 배열의 길이가 달라지게 된다. 예로들어 10개의 원소를 정렬하고자 하는데, 수의 범위가 0~1억이라면 메모리가 매우 낭비가 된다.
즉, Counting Sort가 효율적인 상황에서 쓰려면 수열의 길이보다 수의 범위가 극단적으로 크면 메모리가 엄청 낭비 될 수 있다는 것. 그렇기 때문에 각기 상황에 맞게 정렬 알고리즘을 써야하는데, 퀵 정렬이나 병합정렬 등이 선호되는 이유도 이에 있다.
(Quick 정렬의 경우 시간복잡도 평균값이 𝚶(nlogn) 으로 빠른편이면서 배열도 하나만 사용하기 때문에 공간복잡도는 𝚶(𝑛) 으로 시간과 메모리 둘 다 효율적이라는 점이다.)
그럼 본격적으로 구현을 해보자.
- 구현하기 [Java]
먼저 array 크기(수열의 크기)는 100개로 하고, 수의 범위는 0~30 으로 할 것이다.
public class CountingSort {
public static void main(String[] args) {
int[] array = new int[100]; // 수열의 원소 : 100개
int[] counting = new int[31]; // 수의 범위 : 0 ~ 30
int[] result = new int[100]; // 정렬 될 배열
for(int i = 0; i < array.length; i++) {
array[i] = (int)(Math.random()*31); // 0 ~ 30
}
// Counting Sort
// 과정 1
for(int i = 0; i < array.length; i++) {
// array 의 value 값을 index 로 하는 counting 배열 값 1 증가
counting[array[i]]++;
}
// 과정 2
for(int i = 1; i < counting.length; i++) {
// 누적 합 해주기
counting[i] += counting[i - 1];
}
// 과정 3
for(int i = array.length - 1; i >= 0; i--) {
/*
* i 번쨰 원소를 인덱스로 하는 counting 배열을 1 감소시킨 뒤
* counting 배열의 값을 인덱스로 하여 result에 value 값을 저장한다.
*/
int value = array[i];
counting[value]--;
result[counting[value]] = value;
}
/* 비교 출력 */
// 초기 배열
System.out.println("array[]");
for(int i = 0; i < array.length; i++) {
if(i % 10 == 0) System.out.println();
System.out.print(array[i] + "\t");
}
System.out.println("\n\n");
// Counting 배열
System.out.println("counting[]");
for(int i = 0; i < counting.length; i++) {
if(i % 10 == 0) System.out.println();
System.out.print(counting[i] + "\t");
}
System.out.println("\n\n");
// 정렬된 배열
System.out.println("result[]");
for(int i = 0; i < result.length; i++) {
if(i % 10 == 0) System.out.println();
System.out.print(result[i] + "\t");
}
System.out.println();
}
}
위 코드를 토대로 실행을 해보면 다음과 같이 출력된다. (물론 랜덤값으로 수열을 초기화 했기 때문에 조금씩은 다르나 정렬이 된다는 것을 보여주어야 겠으니..)

매우 잘 정렬된다. 물론 정렬이 잘 되는 것은 볼 수 있으나 속도가 빠른지는 100개 정렬만으로는 감이 안올 것이다. 그러니 범위를 좀 더 넓혀보기도 하고 여러가지 변수 범위를 변경해보시길 바란다.
- 정리
Counting Sort 는 각 배열 원소끼리 직접 비교하는 것이 아닌, 인덱스를 갖고 위치를 찾아나가는 것이다. 위의 예시에서는 비교를 위해 array 와 result 배열이 존재했지만, 수의 범위를 알고있고 입출력만 하는 것이라면 array에 0번째부터 입력하는게 아니라 counting 처럼 입력 받자마자 해당 값을 array 배열의 인덱스를 사용하여 array 배열 값을 증가시킨 뒤, 누적 합 부분을 skip 하고 바로 array[0] 부터 해당 인덱스의 값이 0 이 될 때 까지 인덱스를 출력해주면 된다.
예로들면 이렇게 말이다.
public class counting_sort {
public static void main(String[] args) {
int[] arr = new int[101]; // 수의 범위 : 0 ~ 100
for (int i = 0; i < 50; i++) { // 수열의 크기 : 50
arr[(int) (Math.random() * 101)]++; // 0 ~ 100
}
for(int i = 0; i < arr.length; i++) {
while(arr[i]-- > 0) { // arr 값이 0보타 클 경우
System.out.print(i + " ");
}
}
}
}
필자가 이 방법을 설명하는 이유는, 백준에서 정렬 문제를 풀 때 이 방법이 매우 빠르기 때문이다.
특히, 시간 제한이 매우 빡빡한 경우에는 Arrays.sort() 를 쓰더라도 시간초과가 난다. 특히 최악의 경우 퀵 정렬이라도 시간이 O(n2) 이기 때문에 이를 노리고 저격 데이터가 있을 수 있다. 그러니 앵간한 문제에서는 이 방법을 쓰는 것을 적극 추천한다.
그러나 일반적인 상황이라면 단순 숫자가 아닌 대부분 객체를 갖고 정렬을 하게 된다. 어디까지나 Counting Sort는 특정 타입에 한정되어있기도 하고, 만약 입력되는 수의 개수는 적지만, 수의 범위가 매우 클 경우 심한 메모리 낭비와 더불어 자바에서는 1차원 배열 객체 하나의 크기는 최대 Integer.MAX_VALUE 미만으로만 가능하기 때문에 (배열의 경우 int값으로 색인하며 또한 대부분의 사용자의 heap 메모리가 하나의 배열을 8GB 만큼 큰 메모리를 확보하지 못한다.) 실생활에서는 거의 안쓰인다. 그렇기 때문에 대부분 언어에서는 TimSort나 QuickSort 를 쓰는 것이다.
'알고리즘 > Java' 카테고리의 다른 글
| 자바 [JAVA] - 셸 정렬 (Shell Sort) (18) | 2021.02.18 |
|---|---|
| 자바 [JAVA] - 거품 정렬 (Bubble Sort) (2) | 2021.01.18 |
| 자바 [JAVA] - 삽입 정렬 (Insertion Sort) (8) | 2020.11.30 |
| 자바 [JAVA] - 선택 정렬 (Selection Sort) (10) | 2020.11.14 |
| JAVA [자바] - 소수 구하는 알고리즘 및 구현 (25) | 2020.04.15 |