[백준] 4948번 : 베르트랑 공준 - JAVA [자바]
https://www.acmicpc.net/problem/4948
4948번: 베르트랑 공준
문제 베르트랑 공준은 임의의 자연수 n에 대하여, n보다 크고, 2n보다 작거나 같은 소수는 적어도 하나 존재한다는 내용을 담고 있다. 이 명제는 조제프 베르트랑이 1845년에 추측했고, 파프누티 체비쇼프가 1850년에 증명했다. 예를 들어, 10보다 크고, 20보다 작거나 같은 소수는 4개가 있다. (11, 13, 17, 19) 또, 14보다 크고, 28보다 작거나 같은 소수는 3개가 있다. (17,19, 23) n이 주어졌을 때, n보다 크고, 2n보
www.acmicpc.net
-
문제
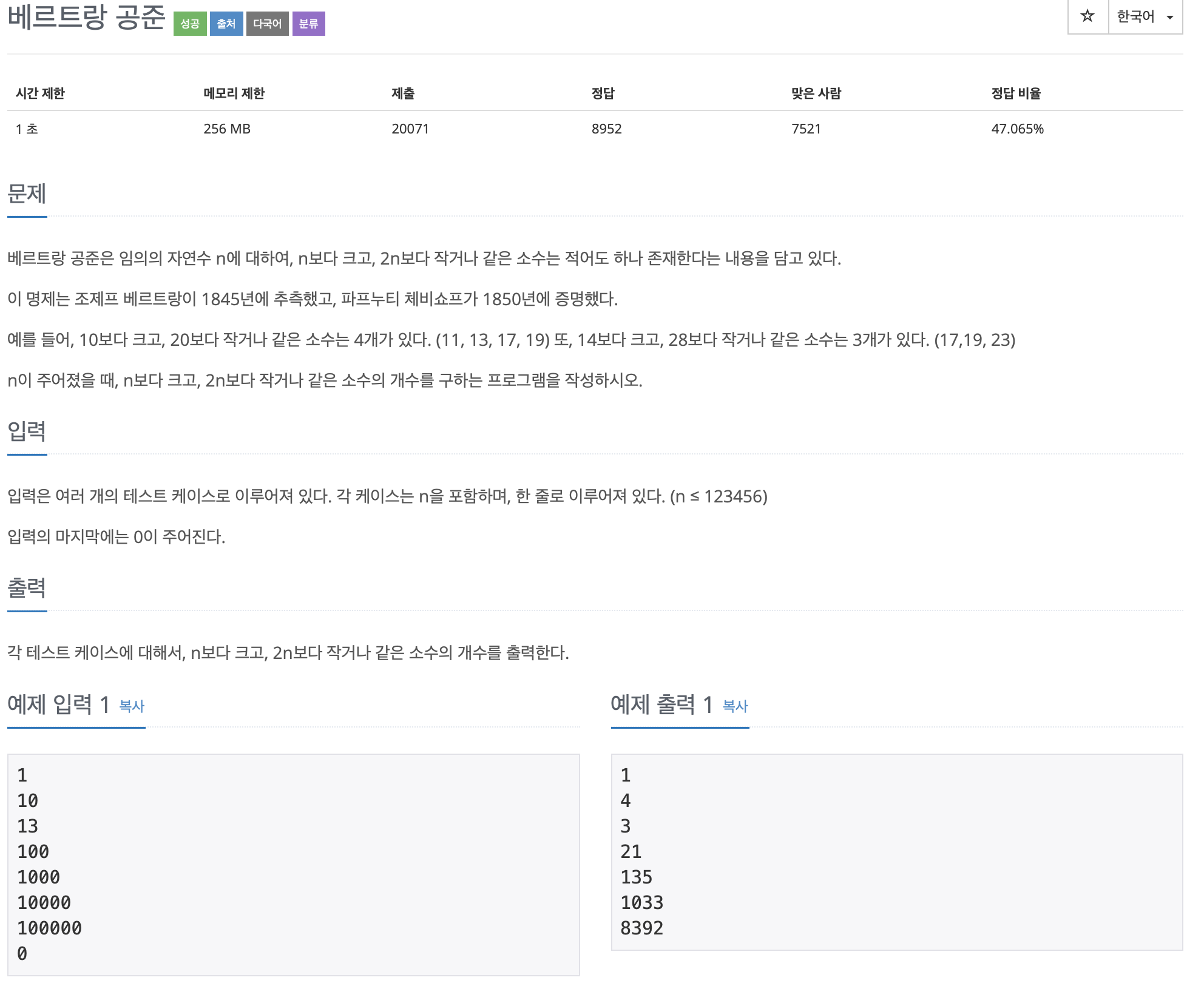
입력이 주어질 때 N ~ 2N 사이에 몇 개의 소수가 있는지 구하는 문제다.
그리 어려운 문제가 아니니 같이 풀어보도록 하자.
- 3가지 방법을 이용하여 풀이한다.
기본적인 알고리즘은 에라토스테네스의 체를 이용하여 소수를 구할 것이다.
위 알고리즘에 대한 글은 아래 포스팅을 참고하면 된다.
https://st-lab.tistory.com/81?category=830901
소수를 구하는 알고리즘 - JAVA [자바]
들어가기 전에 소수 [Prime Number] 소수의 정의는 1보다 큰 자연수 중 1 과 그 수 자기 자신만을 약수로 갖는 자연수를 의미한다는 점은 누구나 알고 있을 것이다. 즉, 소수의 약수는 2개만을 갖고, 그 중 하나는..
st-lab.tistory.com
위 에라토스테네스의 체를 이용하여 boolean 배열로 소수인 경우는 false, 소수가 아닌경우는 true 를 담고 있도록 할 것이다.
그리고 입력 N 이 주어지면 해당 배열에서 index 가 N ~ 2N 까지 순회하면서 false 의 개수를 세어주면 된다.
4가지 방법은 다음과 같이 짤 것이다.
- Scanner 로 입력받는 방법
- BufferedReader 로 입력받는 방법
- BufferedReader 로 입력받되 효율적으로 출력하는 방법
- 3번과 같으나 소수의 개수를 미리 구해놓고 해결하는 방법
- 풀이
- 방법 1
import java.util.Scanner;
public class Main {
/*
n > 123456 이므로 2n 은 최대 246912 이다.
0 부터 시작하므로 246912 + 1
*/
public static boolean[] prime = new boolean[246913];
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
get_prime(); // 소수를 얻는 메소드 실행
while(true) {
int n = in.nextInt();
if(n == 0) break; // n 이 0 일경우 종료
int count = 0; // 소수 개수를 셀 변수
for(int i = n + 1; i <= 2 * n; i++) {
if(!prime[i]) count++;
}
System.out.println(count);
}
}
// 소수를 얻는 메소드
public static void get_prime() {
// 0 과 1 은 소수가 아니므로 ture
prime[0] = prime[1] = true;
for(int i = 2; i <= Math.sqrt(prime.length); i++) {
if(prime[i]) continue;
for(int j = i * i; j < prime.length; j += i) {
prime[j] = true;
}
}
}
}
가장 기본적인 방법이라 할 수 있겠다.
참고로 입력의 범위는 최대 123456 이므로 n = 123456 일 때, 2n 은 246912 이다.
배열 index 는 0 부터 시작하므로 +1 을 한 246913 개의 index 를 갖는 정적 boolean 배열을 생성하는 것이다.
- 방법 2
위 코드에서 Scanner 대신 BufferedReader 로 입력받는 방법이다.
알고리즘 자체는 같으니 별다른 설명은 하지 않겠다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
/*
n > 123456 이므로 2n 은 최대 246912 이다.
0 부터 시작하므로 246912 + 1
*/
public static boolean[] prime = new boolean[246913];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
get_prime(); // 소수를 얻는 메소드 실행
while(true) {
int n = Integer.parseInt(br.readLine());
if(n == 0) break; // n 이 0 일경우 종료
int count = 0; // 소수 개수를 셀 변수
for(int i = n + 1; i <= 2 * n; i++) {
if(!prime[i]) count++;
}
System.out.println(count);
}
}
// 소수를 얻는 메소드
public static void get_prime() {
// 0 과 1 은 소수가 아니므로 ture
prime[0] = prime[1] = true;
for(int i = 2; i <= Math.sqrt(prime.length); i++) {
if(prime[i]) continue;
for(int j = i * i; j < prime.length; j += i) {
prime[j] = true;
}
}
}
}
다만 필자의 다른 포스팅을 보았다면 알 수 있듯이 BufferedReader.readLine() 을 쓸 경우 항상 문자열로만 받기때문에 int 형의 변수로 쓰고싶다면 String 을 int 로 변환시켜주는 Integer.parseInt() 을 써주어야 한다.
- 방법 3
방법 자체는 방법 2와 비슷하지만 더욱 효율적인 알고리즘을 구상해보고자 한다.
일단 우리가 가장 쉽게 볼 수 있는 것은 출력 호출, 즉 System.out.println() 을 반복적으로 출력해주어야 한다.
특히 테스트케이스가 몇 개인지 밝히고 있지않아서 만약 n 이 100만번 입력된다면 출력 또한 100만번 호출되니 너무 비효율적일 것 같다.
그래서 결과를 String 으로 하나로 묶은 다음에 반복문이 종료되면 그동안의 결과들을 한 번에 출력해주면 된다.
위 방법의 해법은 StringBuilder 을 사용하여 하나의 문자열로 묶어주도록 하자.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
/*
n > 123456 이므로 2n 은 최대 246912 이다.
0 부터 시작하므로 246912 + 1
*/
public static boolean[] prime = new boolean[246913];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
get_prime(); // 소수를 얻는 메소드 실행
StringBuilder sb = new StringBuilder();
while(true) {
int n = Integer.parseInt(br.readLine());
if(n == 0) break; // n 이 0 일경우 종료
int count = 0; // 소수 개수를 셀 변수
for(int i = n + 1; i <= 2 * n; i++) {
if(!prime[i]) count++;
}
sb.append(count).append('\n'); // 문자열로 이어준다
}
System.out.print(sb);
}
// 소수를 얻는 메소드
public static void get_prime() {
// 0 과 1 은 소수가 아니므로 ture
prime[0] = prime[1] = true;
for(int i = 2; i <= Math.sqrt(prime.length); i++) {
if(prime[i]) continue;
for(int j = i * i; j < prime.length; j += i) {
prime[j] = true;
}
}
}
}
- 방법 4
여기서 더욱 좋은 방법은 없을까?
아까 방법 3에서는 우리가 출력이 반복되었기 때문에 한 번에 출력하도록 바꿔주었다.
이와같이 반복되는 것이 무엇이 있을까?
잘 보면 우리는 n 을 입력받을 때마다 prime[] 배열에서 n+1 부터 2*n 까지 반복적으로 false 의 개수를 세어준다.
만약에 123456 을 30 번 반복입력받으면 어떻게 될까?
앞서 이미 세어줬음에도 계속 반복문이 돌 때마다 세어준다.
그러면 각 반복문마다 세지 말고 처음에 각 입력값마다 소수의 개수가 몇 개인지 센 배열이 있다면 어떨까?
위를 적용한다면 굳이 반복문마다 셀 필요 없이 해당 값의 배열에 저장된 수를 출력하면 되니 매우 빠를 것이다.
그러면 위 발상을 한 번 적용시켜보자.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
/*
n > 123456 이므로 2n 은 최대 246912 이다.
0 부터 시작하므로 246912 + 1
*/
public static boolean[] prime = new boolean[246913];
/*
1 부터 누적하여 각 index 까지의
소수의 개수를 담을 배열
*/
public static int[] count_arr = new int[246913];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
get_prime(); // 소수를 얻는 메소드 실행
get_count(); // 소수의 개수가 저장된 배열을 얻는 메소드 실행
StringBuilder sb = new StringBuilder();
while(true) {
int n = Integer.parseInt(br.readLine());
if(n == 0) break; // n 이 0 일경우 종료
// 2n 까지의 소수의 개수 - n 까지의 소수의 개수
sb.append(count_arr[2 * n] - count_arr[n]).append('\n');
}
System.out.print(sb);
}
// 소수를 얻는 메소드
public static void get_prime() {
// 0 과 1 은 소수가 아니므로 ture
prime[0] = prime[1] = true;
for(int i = 2; i <= Math.sqrt(prime.length); i++) {
if(prime[i]) continue;
for(int j = i * i; j < prime.length; j += i) {
prime[j] = true;
}
}
}
// 소수의 개수를 얻는 메소드
public static void get_count() {
int count = 0;
for(int i = 2; i < prime.length; i++) {
if(!prime[i]) count++; // 소수일 경우 count를 증가시킨다
/*
0 ~ i 까지 소수의 개수 = count
count 값을 count_arr 의 i 에 저장한다
*/
count_arr[i] = count;
}
}
}
- 성능

위에서 부터 순서대로
채점 번호 : 19383425 - 방법 4 (BufferedReader + StringBuilder + count_arr)
채점 번호 : 19383003 - 방법 3 (BufferedReader + StringBuilder)
채점 번호 : 19382767 - 방법 2 (BufferedReader)
채점 번호 : 19382642 - 방법 1 (Scanner)
보다시피 입출력의 성능차이와 알고리즘에 따라 시간이 달라질 수 있음을 알 수 있다.
- 정리
오늘은 조금 다양한 방법들을 제시했다.
물론 필자의 방법보다 더욱 좋은 방법들이야 매우 많다.
다만 필자의 방법들을 보고 다양하게 문제를 접근할 수 있다는 것을 알았으면 한다.
'JAVA - 백준 [BAEK JOON] > 기본 수학 2' 카테고리의 다른 글
| [백준] 11653번 : 소인수분해 - JAVA [자바] (0) | 2021.01.09 |
|---|---|
| [백준] 9020번 : 골드바흐의 추측 - JAVA [자바] (16) | 2020.05.05 |
| [백준] 1929번 : 소수 구하기 - JAVA [자바] (18) | 2020.04.21 |
| [백준] 2581번 : 소수 - JAVA [자바] (20) | 2020.04.21 |
| [백준] 1978번 : 소수 찾기 - JAVA [자바] (20) | 2020.04.08 |