[백준] 1978번 : 소수 찾기 - JAVA [자바]
https://www.acmicpc.net/problem/1978
1978번: 소수 찾기
첫 줄에 수의 개수 N이 주어진다. N은 100이하이다. 다음으로 N개의 수가 주어지는데 수는 1,000 이하의 자연수이다.
www.acmicpc.net
- 문제

드디어 새로운 카테고리의 첫 문제!
소수 찾기다.
당연하겠지만 여기서 말하는 소수는
0.001, 0.235 같은 decimals 가 아닌 1과 자기 자신만을 약수로 갖는 자연수를 의미한다.
- 2가지 입력방법을 이용하여 풀이한다.
Scanner 로 입력받아 연산하는 방법과 BufferedReader 로 입력받아 연산하는 방법, 두 가지 방법을 통해 풀이해보고자 한다.
- 소수 판별 방법
소수 판별법은 정말 여러가지가 있다.
그 중 대표적인 방법 3가지를 알아보려 한다.
방법 1 : 기본 판별 법
기본적인 소수 판별은 그렇게 어렵지 않다.
1 과 자기 자신만을 약수로 갖기 때문에 2 부터 판별하려는 수 직전까지 하나씩 나눠보면서 나누어 떨어지는 수가 없다면 소수고, 나누어 떨어지는 수가 있다면 소수가 아닐 것이다.
즉 아래와 같이 짤 수 있다.
Number 이라는 숫자를 판별한다고 가정한다.
boolean is_Prime(int Number) {
// 1 은 소수가 아니다.
if(Number == 1){
return false;
}
// 2 ~ Number-1 까지 중 나누어 떨어지는 약수가 있는지 판별
// Number = 2 의 경우는 자연스럽게 for문을 검사하지 않게 됨
for(int i = 2; i < Number; i++) {
if(N % i == 0) return false;
}
// 위 두 조건에 걸리지 않으면 소수다.
return true;
}
반드시 유의할 점은 1 은 소수가 아니다.
그러므로 판별 할 수가 1 일 경우를 예외처리 해줄 필요가 있다.
그리고 2 부터 N-1 까지 값을 N 에 나눠서 나머지가 있는지를 검사하는 방법이다.
이 방법의 경우 시간복잡도는 O(N) 이다.
방법 2 : 제곱근을 이용한 기본 판별법
방법 1 에서 조금 더 효율적으로 판별할 수 있는 방법이 있다.
아주 단순한 방법이다.
생각해보자. 소수를 판별한다는 것은 결국 1 과 자기 자신만을 약수로 가져야 한다.
여기서 포인트는 '약수'라는것이다.
예로들어 11 이라는 수를 판별한다고 생각해보자.
방법 1 로 한다면 2 부터 10 까지 하나씩 나눠보면서 나누어 떨어지는 수가 있는지 검사할 것이다.
11 % 2 ⇨ 약수 아님
11 % 3 ⇨ 약수 아님
11 % 4 ⇨ 약수 아님
11 % 5 ⇨ 약수 아님
11 % 6 ⇨ 약수 아님
11 % 7 ⇨ 약수 아님
11 % 8 ⇨ 약수 아님
11 % 9 ⇨ 약수 아님
11 % 10 ⇨ 약수 아님
∴ 11 은 소수
그런데 가만히 생각해보면 4 이상의 수는 사실 검사 할 필요가 없다.
생각해보자.
Number 을 A × B 의 합성수 (Number = A × B) 라고 볼 때 아래와 같이 부등식을 세울 수 있다.
⇨ ( 1 ≤ A, B < Number )
여기서 만약 A 와 B 가 Number 의 제곱근보다 커지면 위 부등식에 모순이 생긴다.
A, B > sqrt( Number )
↳ A × B > Number
위 식은 결국 A × B = Number 라는 식과 모순이므로 다음과 같은 결론을 내릴 수 있다.
∴ 합성수 Number = A × B 에서 A 와 B 중 적어도 하나는 Number 의 제곱근보다 작거나 같다.
즉, 11 을 4 이상으로 나누려는 수가 11 의 제곱근보다 크기 때문에 몫은 11 의 제곱근보다 작은수가 된다.
결과적으로 2 또는 3 가 몫이 되거나 나누어 떨어지지 않는 수이기 때문에 4 이상의 수를 검사할 필요가 없다.
다른 예로 12 를 가정해보자. 12 의 약수는 아래와 같다.
1, 2, 3, 4, 6, 12
그리고 12 의 제곱근은 약 3.46 이다.
그러면 위 공식에 그대로 적용해본다면
1, 2, 3 까지는 나누어 떨어지는 수가 각 각 12, 6, 4 에 대응된다.
그리고 4 이상부터 검사하면 아래와 같다.
12 ÷ 4 = 3 ... 0 ⇨ 약수
12 ÷ 5 = 2 ... 2 ⇨ 약수 아님
12 ÷ 6 = 2 ... 0 ⇨ 약수
12 ÷ 7 = 1 ... 5 ⇨ 약수 아님
12 ÷ 8 = 1 ... 4 ⇨ 약수 아님
12 ÷ 9 = 1 ... 3 ⇨ 약수 아님
12 ÷ 10 = 1 ... 2 ⇨ 약수 아님
12 ÷ 11 = 1 ... 1 ⇨ 약수 아님
즉, 12 의 제곱근 이상의 수로 나누면 두 가지 경우밖에 없다.
1. 이전의 검사한 수 중 약수인 수를 약수로 갖는다.
2. 약수가 아니다.
그렇기 때문에 소수를 판별할 때 굳이 Number - 1 까지가 아닌 Number 의 제곱근 까지만 검사하면 된다.
위 정리를 이용하여 검사한다면 아래와 같이 짤 수 있다.
boolean is_Prime(int Number) {
// 1 은 소수가 아니다.
if(Number == 1){
return false;
}
// 2 ~ Number의 제곱근까지 중 나누어 떨어지는 약수가 있는지 판별
// Number = 2 의 경우는 자연스럽게 for문을 검사하지 않게 됨
for(int i = 2; i <= Math.sqrt(Number); i++) {
if(N % i == 0) return false;
}
// 위 두 조건에 걸리지 않으면 소수다.
return true;
}
그리고 이 방법의 경우 시간 복잡도는 O(√N) 으로 방법 1 에 비해 더욱 좋은 효율을 볼 수 있다.
방법 3 : 에라토스테네스의 체
가장 대표적인 방법 중 하나다.
원리는 간단하다.
만약 여러개의 소수를 구하고 싶을 때 체를 거르듯이 하는 방법을 쓰면 매우 쉽게 판별 할 수 있다.
방법은 다음과 같다.
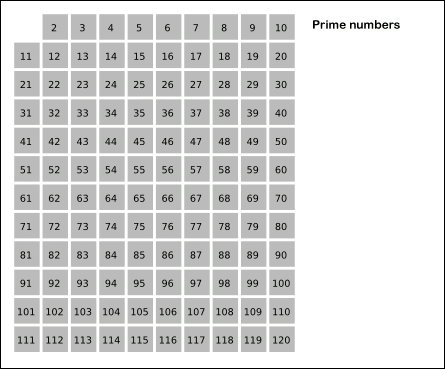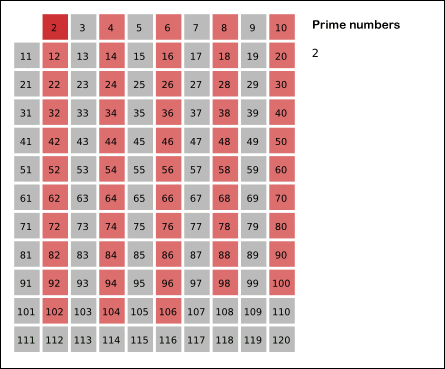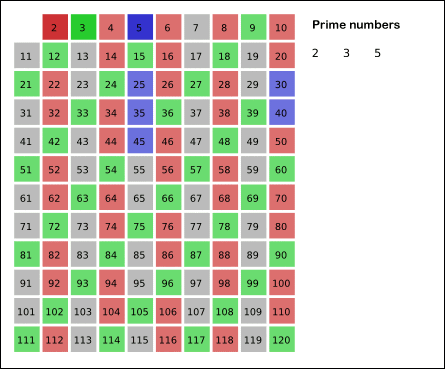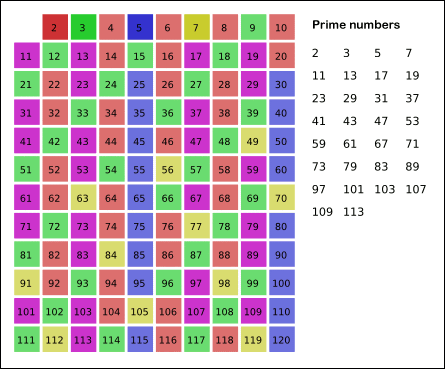
즉 2 를 제외한 2의 배수인 수를 모두 거르고,
3 을 제외한 3 의 배수를 모두 거르고,
( 4 는 2 의 배수에서 걸러졌으므로 Pass )
5 를 제외한 5 의 배수를 모두 거르고,
이런식으로 반복하는 하는 것이다.
그리고 이 방법 또한 마찬가지로 방법 2를 적용시켜 구하려는 범위의 최댓값의 제곱근까지만 반복하면 된다.
즉, 위에서 2 ~ 120 까지의 수 중 소수를 찾고 싶다면
120 의 제곱근인 10.95... 결과적으로 10 까지만 거르면 나머지 체크가 안된 수들이 소수가 되는 것이다.
그러면 1 ~ 10000 까지의 수 중 소수만을 True 값을 갖고있는 배열을 하나 만들어보자.
// 1 ~ Max 범위
// 소수인 수 = false
// 소수가 아닌 수 = true
public boolean[] make_prime(int Max) {
boolean[] Prime = new boolean[Max + 1]; // 0 부터 시작하므로 +1
// 0 과 1 은 소수가 아니므로 true
Prime[0] = true;
Prime[1] = true;
for(int i = 2; i <= Math.sqrt(Max); i++) {
// 이미 걸러진 배열일 경우 다음 반복문으로 건너뜀
if(Prime[i] = true) {
continue;
}
/*
정석대로라면 j = i * 2 부터 시작이지만
이미 2의 배수가 걸러졌기때문에
i 의 제곱수부터 시작해도 된다.
*/
for(int j = i * i; j < Max + 1; j = j + i) {
Prime[j] = true;
}
}
// 배열 index 가 소수라면 false 로, 아니라면 true 로 완성됨
return Prime;
}
위와 같이 짤 수 있다.
위 방법의 장점은 방법 1, 2 보다 시간복잡도가 좋다.
방법 3의 경우 O(n ㏒ (㏒ n)) 의 시간 복잡도를 갖고 있다.
엥? 방법 1이나 2가 그러면 시간복잡도가 더 좋은거 아닌가요? 라고 한다면,
방법 3은 하나의 수에 대한게 아니라 1 ~ N 까지의 수 중 모든 소수를 구하는 것이다.
만약 방법 1 과 2를 1 ~ N 까지의 수 중 모든 소수를 구하라고 하면 시간복잡도는 다음과 같이 된다.
방법 1 : O(N²)
방법 2 : O(N√N)
방법 3 : O(N ㏒ (㏒ N))
그래프로 그려본다면 다음과 같을 것이다.

초록색 : 방법 1
노란색 : 방법 2
보라색 : 방법 3
위의 3 가지 방법은 앞으로 소수 구하는 문제들에서 매우 유용하므로 잘 익혀두길 바란다.
이번 문제의 풀이에서는 방법 2를 쓸 것이다.
- 풀이
- 방법 1
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
int count = 0;
for(int i = 0; i < N; i++) {
// 소수인경우 true, 아닌경우 false
boolean isPrime = true;
int num = in.nextInt();
if(num == 1) { // 1 인경우 다음 반복문으로
continue;
}
for(int j = 2; j <= Math.sqrt(num); j++) {
if(num % j == 0) {
isPrime = false; // 소수가 아니므로 false 로 바꿔줌
break;
}
}
if(isPrime) { // 소수인경우 count 값 1 증가
count++;
}
}
System.out.println(count);
}
}
가장 기본적인 방법이다.
위 소수 찾는 방법에서 설명한 방법 2를 거의 그대로 갖고왔다.
아마 어렵지 않게 이해했으리라 본다.
- 방법 2
BufferedReader 을 쓰는 방식이다.
그리고 반드시 자료형 타입을 잘 보아야 한다.
br.readLine() 은 문자열로 데이터를 읽으니 반드시 꺼내서 쓸 때 int 형으로 쓰고자 한다면 Integer.parseInt()로 String 을 int 형으로 변환시켜준다.
다만, 필자는 StringTokenizer 를 통해 문자열을 분리해줄 것이다.
이 과정에서 StringTokenizer 자체가 토큰이 남아있는지 여부를 true, false 로 반환시켜주는 hasMoreTokens() 라는 메소드를 갖고 있기 때문에 굳이 N 을 쓸 필요가 없기에 N 은 입력만 받고 따로 변수를 두지 않는다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
br.readLine(); // N 은 쓰지 않음.
int count = 0;
StringTokenizer st = new StringTokenizer(br.readLine()," ");
while(st.hasMoreTokens()) {
// 소수인경우 true, 아닌경우 false
boolean isPrime = true;
int num = Integer.parseInt(st.nextToken());
if(num == 1) {
continue;
}
for(int i = 2; i <= Math.sqrt(num); i++) {
if(num % i == 0) {
isPrime = false;
break;
}
}
if(isPrime) {
count++;
}
}
System.out.println(count);
}
}
위 코드를 실행하면 Scanner 보다 BufferedReader 가 속도가 빠르니 시간이 단축되므로 매우 좋다.
- 성능 차이

위에서 부터 순서대로
채점 번호 : 19009698 - BufferedReader
채점 번호 : 19009677 - Scanner
- 정리
오늘은 소수를 어떻게 구할지, 또는 판별할지를 알아보았다.
물론 필자처럼 구하지 않고 1 ~ 1000까지 에라토스테네스의 체를 이용하여 소수만 체크되어있는 배열을 구한 뒤, 숫자를 입력받으면 배열의 index 와 비교하여 판별할 수도 있다.
여러가지 방법이 있으니 다양하게 시도해보아도 좋을 것 같다.
'JAVA - 백준 [BAEK JOON] > 기본 수학 2' 카테고리의 다른 글
| [백준] 11653번 : 소인수분해 - JAVA [자바] (0) | 2021.01.09 |
|---|---|
| [백준] 9020번 : 골드바흐의 추측 - JAVA [자바] (16) | 2020.05.05 |
| [백준] 4948번 : 베르트랑 공준 - JAVA [자바] (14) | 2020.04.24 |
| [백준] 1929번 : 소수 구하기 - JAVA [자바] (18) | 2020.04.21 |
| [백준] 2581번 : 소수 - JAVA [자바] (20) | 2020.04.21 |