[백준] 2839번 : 설탕 배달 - JAVA [자바]
https://www.acmicpc.net/problem/2839
2839번: 설탕 배달
문제 상근이는 요즘 설탕공장에서 설탕을 배달하고 있다. 상근이는 지금 사탕가게에 설탕을 정확하게 N킬로그램을 배달해야 한다. 설탕공장에서 만드는 설탕은 봉지에 담겨져 있다. 봉지는 3킬로그램 봉지와 5킬로그램 봉지가 있다. 상근이는 귀찮기 때문에, 최대한 적은 봉지를 들고 가려고 한다. 예를 들어, 18킬로그램 설탕을 배달해야 할 때, 3킬로그램 봉지 6개를 가져가도 되지만, 5킬로그램 3개와 3킬로그램 1개를 배달하면, 더 적은 개수의 봉지를 배달할 수
www.acmicpc.net
-
문제

이번 문제는 나름! 수학적 사고를 테스트하는 문제다.
여기서 주의해야할 점은 N 에 정확히 맞추어 봉지의 개수가 최소가 되는 값을 구하는 것이다.
- 2가지 입력방법을 이용하여 풀이한다.
Scanner 로 입력받아 연산하는 방법과 BufferedReader 로 입력받아 연산하는 방법, 두 가지 방법을 통해 풀이해보고자 한다.
- 알고리즘 [ 풀이 방법 ]
이번 문제는 막상 암산으로 하기에는 조금 버거운 문제다.
물론 대부분은 N 이 주어지면 암산으로는 금방 봉지의 최소 개수를 구하지만 막상 알고리즘을 떠올리려 하면 잘 생각나지 않는다.
물론 가장 쉬운 방법은 재귀나 반목문을 통해서 모든 경우의 수를 구한다음 최솟값을 찾아낼 수는 있으나, 너무 비효율적인 알고리즘이라는 것은 누구나 알 것이고... 그렇기에 수학적으로 한 번 풀어보자.
사실 이번 문제는 다른 문제들처럼 막상 경우의 수를 쭉 나열해서 규칙을 찾는다면 그리 어렵지 않다.
그러니 아래 설명을 통해 이해해보도록 하자.
1. 먼저 설탕 봉지는 크게 두 가지, 3kg 과 5kg 이렇게 있다.
여기서 봉지의 개수를 최소화하려면 최대한 5kg 봉지로 구성해야한다는 점은 누구나 알 것이다.
그래서 N 이 3일 때부터 몇가지 수를 나열하기 전에 5 로 나누어 떨어지는 수를 하나의 구간으로 나누어서 표를 그려보자.
그럼 아래처럼 표가 그려질 것이다.

2. 그리고 n/5 의 값과 n%5 의 값을 채워보자.
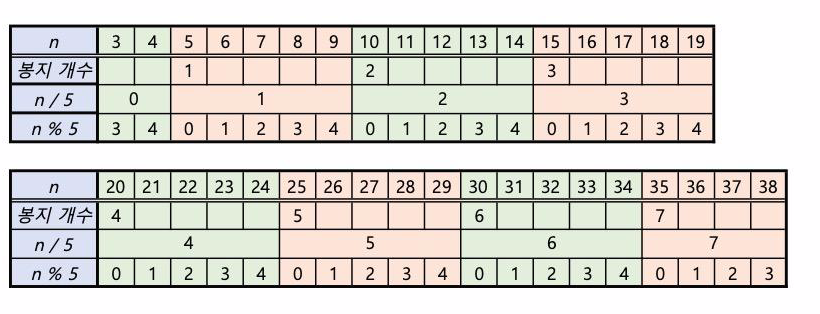
3. 그리고 나머지 수를 채워야하는데, 위 표에서 우리는 간단하게 먼저 채울 수 있는 수들이 있다.
생각해보자.
우리는 봉지의 개수를 최소화하는 것이 목적이다.
이미 5의 배수에는 5로 나눈 몫의 값이 들어가 있다.
그렇다면 5로 나누어 떨어지는 수의 +3 을 한 값은 당연히 봉지 개수가 최소가 아닐까?
즉,
5 + 3
10 + 3
15 + 3
20 + 3
...
5의 배수 + 3 의 자리는 5의 배수에 있던 값의 +1 개수가 되는 것이다.
아래 표를 보면 바로 이해 될 것이다.
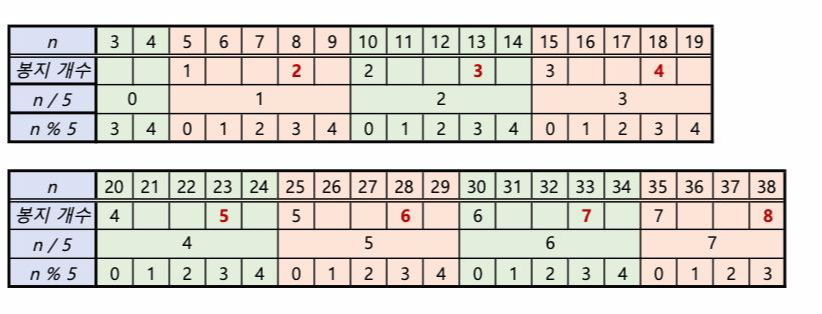
4. 그리고 다음으로 채울 부분은 3번 과정이랑 유사하다.
3과 6은 5로는 못 채우는 수라는 것은 모두가 알고 있다.
그렇다면, 11, 16, 21 등 n이 5의 배수 + 1 이라면?
답은 간단하다. n = 3 일때는 봉지가 1 개,
n = 6 일때 봉지가 2 개였고,
n = 6 부터 +5 씩 증가할 때 마다 봉지의 개수는 1 씩 증가한다.
즉, n 이 3, 6, 그리고 5의배수 + 1 인 부분을 채운다면 다음과 같을 것이다.

5. 거의 다 왔다.
다음으로 채울 부분은 n 이 5의 배수 - 1 일 때이다. 4번 과정과 유사하다.
다만 5의 배수 - 1 값 중 n = 4 일 때는 어떤 봉지로도 정확하게 나누어 떨어지지 않는다.
( 5의 배수 - 1 ) 이 성립하는 것은 n = 9 부터이므로 9 부터 채워준다.
이때 9 는 3kg 봉지 3 개가 최소 개수라는 것은 모두가 알 것이다.
즉, n = 9 부터 +5 씩 증가할 때마다 봉지의 개수는 3 에서 1 씩 증가하는 것이다.
아래 표를 보자.
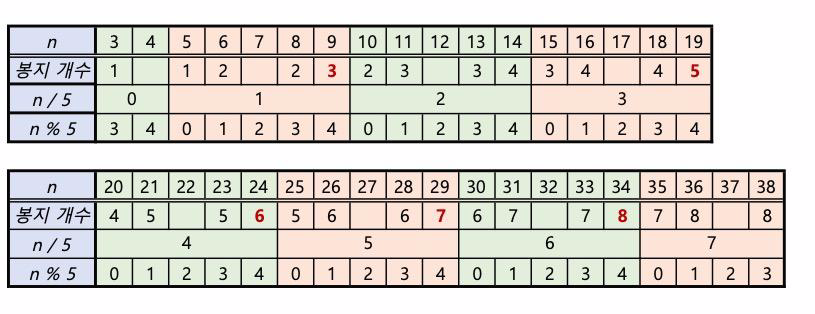
6.
12 + 5의 배수도 이전의 방법처럼 똑같이 채워준다.
12 의 최소 봉지 개수는 4개이고,
n = 12 부터 +5 씩 증가할 때마다 봉지는 +1 씩 증가할 것이다.
그리고 채우다 보면 알겠지만, 4 와 7 은 3kg 봉지와 5kg 봉지로 구성할 수 없다.
그렇기에 n = 4, n = 7 에는 -1 을 채워준다.
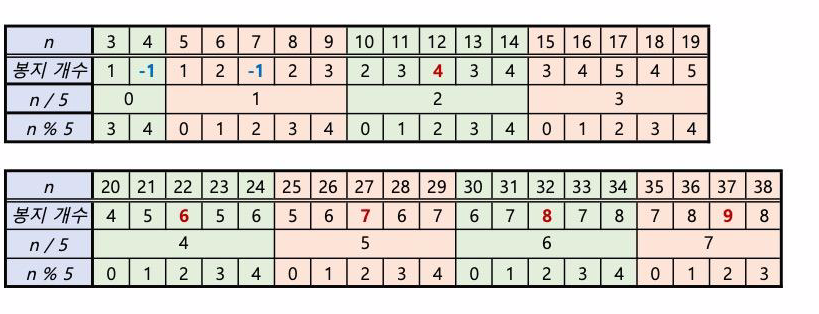
7.
이렇게 다 구성된 표를 한 번 다시 보자.
무언가 규칙이 보이지 않는가?
나머지와 몫의 규칙을 잘 보시길 바란다.
n ≥ 3 일 때
< 5의 배수 + 1 번째 >의 봉투의 개수는 (n / 5) + (n % 5) 이다.
그리고 n % 5 는 항상 1 이다.
또한 중요한 점은 해당 값은 5의 배수 +3 번째의 봉투의 개수와 같다.
즉, (5의 배수 + 1) 과 (5의 배수+ 3) 은 5로 나눈 몫의 + 1 이 봉지 개수가 되는 것이다.
표로 보여주자면 아래와 같다.

이는 n = 3 일 때도 마찬가지이다.
n = 3 일 때 5로 나누면 0이 되고, 여기에 + 3 일 때 봉지 개수는 몫의 + 1 이 되므로 1 이 결과 값이 된다.
이를 조건문으로 나타낸다면?
if ( (n % 5) == 1 || (n % 5) == 3 ) {
return (n / 5) + 1 ;
}
즉, n 이 5의 배수 + 1 또는 + 3 이라면 ( 5 로 나눈 나머지가 1 또는 3 이라면 )
n 을 5 로 나눈 몫 + 1 이 설탕 봉지의 최소 개수가 된다.
8.
그럼 마찬가지로 다른 곳도 규칙을 찾을 수 있겠다.
n ≥ 8 일 때
< 5의 배수 + 2 번째 >의 봉투의 개수는 (n / 5) + (n % 5) 이다.
이때 n % 5 는 항상 2 이다.
또한 중요한 점은 해당 값은 5의 배수 +4 번째의 봉투의 개수와 같다.
즉, (5의 배수 + 2) 과 (5의 배수+ 4) 은 5로 나눈 몫의 + 2 가 봉지 개수가 되는 것이다.
표로 보여주자면 다음과 같다.
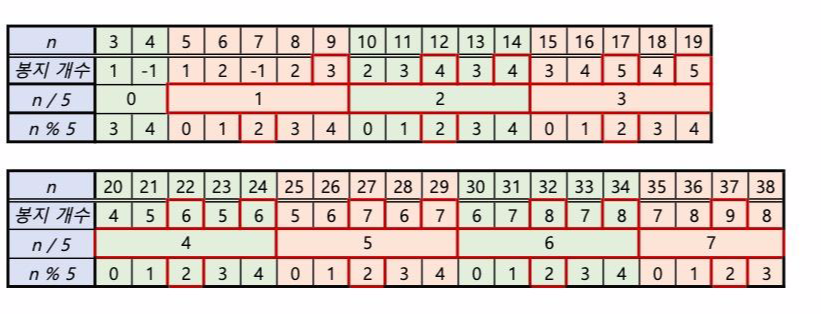
이를 조건문으로 짜면 다음과 같을 것이다.
if( (n % 5) == 2 || (n % 5) == 4 ) {
return (n / 5) + 2;
}
즉, n 이 5의 배수 + 2 또는 + 4 이라면 ( 5 로 나눈 나머지가 2 또는 4 이라면 )
n 을 5 로 나눈 몫 + 2 이 설탕 봉지의 최소 개수가 된다.
9. 그리고 n 이 4 일 때와 7 일 때는 3kg 봉지와 5kg 봉지로 이룰 수 없기 때문에 -1 이 나오도록 조건문을 달아 주어야 한다.
또한 5의 배수는 5로 나눈 몫만 출력하면 되기에 해당 조건 또한 출력해준다.
if ( n == 4 || n == 7 ) {
return -1;
}
else if ( n % 5 == 0 ) {
return (n / 5);
}
이런식으로 구조를 짜면 된다.
하나로 정리해보자.
우리는 크게 4가지 케이스로 나누었다.
- n 이 4 또는 7 인 경우
- n 이 5의 배수인경우 ( 5로 나눈 나머지가 0 인 경우 )
- n 이 5의 배수 + 1 또는 5의 배수 + 3 인 경우 ( 5로 나눈 나머지가 1 또는 3 인 경우 )
- n 이 5의 배수 + 2 또는 5의 배수 + 4 인 경우 ( 5로 나눈 나머지가 2 또는 4 인 경우 )
이를 조건문으로 묶으면 아래와 같다.
if (n == 4 || n == 7) {
return -1;
}
else if (n % 5 == 0) {
return (n / 5);
}
else if (n % 5 == 1 || n % 5 == 3) {
return (n / 5) + 1;
}
else if (n % 5 == 2 || n % 5 == 4) {
return (n / 5) + 2;
}
그럼 이를 토대로 한 번 완전한 코드를 짜보자.
아 그리고 혹여나 3kg 하고 5kg 으로 구성하지 못하는 수가 4 하고 7 말고 더 있지 않냐는 궁금증이 있다면 아래 더보기 누르면 된다.
일단 대답은 "없을 확률이 0에 가깝다"다.
왜 그런지 살짝 언급하겠다.
n ≥ 3 일 때 3 과 5로 구성할 수 없는 수가 4 하고 7 밖에 없나요?
일단 아까 잠깐 언급했듯이 없을 확률이 0에 가깝다.
이는 골드바흐의 추측이라는 개념을 알고 있다면 쉽게 접근할 수 있는데, 기본적으로 이 명제는 다음과 같다.
"두 소수의 합으로 표현 가능한 모든 정수는, 모든 항이 1이 될 때까지 원하는 만큼 얼마든지 많은 개수의 소수의 합으로 분해할 수 있다."
이는 처음 골드바흐가 추측한 명제다.
현재는 골드바흐의 추측을 아래와 같이 설명한다.
"2보다 큰 모든 짝수는 두 소수의 합으로 표현가능하다."
이는 흔히 강한 골드바흐의 추측이라고 하는데,
위 명제가 참이라면 홀수의 경우 3을 더하면 되고, 짝수의 경우는 2를 더하면 세 소수의 합으로도 표현가능해지기 때문이다.
이 강한 골드바흐의 추측은 증명되기가 힘든 이유가 크게 두 가지가 있다.
1. 소수의 규칙성이 증명되지 않았다.
2. 2보다 큰 짝수의 자연수의 개수는 무한대다. (즉, 끝이 없다.)
소수의 규칙성이 증명된다면야 다음 문제점도 풀릴 가능성이 매우 높아지지만 아직 첫 번째 문제점조차 해결되지 못했다.
일단 서론이 길었고, 본론으로 가자면
일단 컴퓨터로 1018( 엑사라고 한다나 뭐라나.. ) 까지는 참인 것이 밝혀졌고 여러 증명들이 있으나, 어디까지나 약한 골드바흐의 추측의 증명일 뿐 강한 골드바흐의 추측이 증명된 것은 아니다.
그러나 사실상 참이라고 보고는 있다.
즉 2 이상의 모든 짝수는 소수의 합으로 나타낼 수 있다는 것이다.
또한 홀수의 경우는 위 명제에 3을 더하면 되므로 사실상 모든 수가 소수의 합으로 이루어져 있음을 알 수 있다.
이는 소인수 분해를 해보면 알 것이다.
위 문제에서는 3하고 5가 주어졌다. 위 이론에 적용해본다면, 이 수의 합, 8 이상의 모든 자연수는 소수의 합으로 나타낼 수 있다.
그렇기 때문에 주어진 두 수의 합 이하의 경우를 제외한다면, 모든 수는 소인수 분해를 3과 5로 나눌 수 있다는 것이다.
그렇기 때문에 8 이상의 값에서 3과 5로 구성되지 못하는 수는 0에 가깝다고 한 것이다.
- 풀이
- 방법 1
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
if (N == 4 || N == 7) {
System.out.println(-1);
}
else if (N % 5 == 0) {
System.out.println(N / 5);
}
else if (N % 5 == 1 || N % 5 == 3) {
System.out.println((N / 5) + 1);
}
else if (N % 5 == 2 || N % 5 == 4) {
System.out.println((N / 5) + 2);
}
}
}
가장 기본적인 방법이다.
막상 수학적으로 접근하고 나니까 코드가 훨씬 간결해지지 않았는가?
- 방법 2
BufferedReader 을 쓰는 방식이다.
그리고 반드시 자료형 타입을 잘 보아야 한다.
br.readLine() 은 문자열로 데이터를 읽으니 반드시 꺼내서 쓸 때 int 형으로 쓰고자 한다면 Integer.parseInt()로 String 을 int 형으로 변환시켜준다.
알고리즘은 다른 것이 없다.
import java.io.InputStreamReader;
import java.io.BufferedReader;
import java.io.IOException;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
if (N == 4 || N == 7) {
System.out.println(-1);
}
else if (N % 5 == 0) {
System.out.println(N / 5);
}
else if (N % 5 == 1 || N % 5 == 3) {
System.out.println((N / 5) + 1);
}
else if (N % 5 == 2 || N % 5 == 4) {
System.out.println((N / 5) + 2);
}
}
}
위 코드를 실행하면 물론 Scanner 보다 BufferedReader 가 속도가 빠르니 시간이 단축되므로 시간 단축에 의의를 둔다면 매우 효과적인 방법이다.
- 성능 차이

위에서 부터 순서대로
채점 번호 : 18744992 - BufferedReader
채점 번호 : 18744986 - Scanner
시간을 보면 BufferedReader 와 Scanner 의 성능차이를 볼 수 있다.
- 정리
수학문제는 몇 가지 특징이 있다.
그중 가장 대표적인게 규칙성이다.
필자가 설명한 것처럼 어느정도 일정 수를 나열해서 표로 나타내다보면 수식에 규칙이 있건, 수 자체에 규칙이 있건 뭐든간에 규칙이 있다.
(규칙이 없다면 그것은 난수를 풀라는 것이니.. 어쩌면 당연한 소리일지도 모르겠다.)
뭐 반복문으로 짜는 사람부터 다양한 방법으로 풀이하지만, 아무래도 필자가 지금 설명한 방법이 가장 알고리즘을 이해하기 쉬울 거라 생각해서 위 방법으로 설명을 한 것이다.
물론 위 과정이 귀찮다면 반복문 또는 재귀로 모든 경우의 수를 다 탐색하는 방법도 있다.
그러나 재귀는 필요없는 루트까지 탐색하게 되고, 무엇보다 수가 커지면 재귀가 깊어지면서 stackoverflow 를 뱉어낼 수 있고, 반복문은 수가 매우 큰 수일 경우 그만큼 반복하기 때문에 탐색시간이 길어진다.
굳이 O(1)의 시간복잡도를 두고 O(N)의 알고리즘을 사용할 필요는 없지 않은가.
'JAVA - 백준 [BAEK JOON] > 기본 수학 1' 카테고리의 다른 글
| [백준] 10250번 : ACM 호텔 - JAVA [자바] (11) | 2020.04.04 |
|---|---|
| [백준] 2869번 : 달팽이는 올라가고 싶다 - JAVA [자바] (38) | 2020.04.01 |
| [백준] 1193번 : 분수찾기 - JAVA [자바] (41) | 2020.03.31 |
| [백준] 2292번 : 벌집 - JAVA [자바] (17) | 2020.03.29 |
| [백준] 1712번 : 손익분기점 - JAVA [자바] (43) | 2020.03.27 |