[백준] 6549번 : 히스토그램에서 가장 큰 직사각형 - JAVA [자바]
https://www.acmicpc.net/problem/6549
6549번: 히스토그램에서 가장 큰 직사각형
입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤
www.acmicpc.net
- 문제

히스토그램 내의 가장 큰 넓이를 구하는 문제는 엄청 유명한 문제라 알고리즘을 많이 접해보았다면 한 번쯤은 접해보았을 문제다.
- 알고리즘 [접근 방법]
이 번 문제의 경우 풀이 방법 자체는 대표적으로 두 가지 방식이 있다.
먼저 이 문제의 카테고리 처럼 분할정복으로 풀이하는 방식, 그리고 스택 자료구조를 이용한 풀이 방식이 있다. 이 번에는 분할 정복 카테고리에 있긴 하지만 스택을 이용한 풀이 방식도 대표적인 방식이고 훨씬 간결하며 좋기에 두 가지 방식 모두 다뤄보도록 하겠다.
(분할 정복의 단점을 개선시켜 세그먼트 트리로도 풀 수는 있으나, 아직 해당 카테고리는 다루지 않았기 때문에 따로 다루지는 않겠다.)
[분할 정복 방식]
분할 정복으로 접근하는 방식도 엄청나게 다양하다. 예로들어 높이를 고정시켜 풀이할 수도 있고, 구간 내 가장 작은 높이의 블럭을 기준으로
분할하여 풀이할 수 있으며, 그냥 구간 내의 가운데를 기준으로 분할하여 풀이하는 방법도 있다.
아마 여러분이 구글링을 통해 해당 문제 풀이 방법을 보면 풀이 방식이 다 다를 것이다. 그 이유가 위 처럼 어떤 것을 기준으로 재귀적으로 분할하여 들어 갈 것인지가 다르기 떄문이다.
그 중 오늘 필자가 분할 정복 풀이 방식에서는 가장 직관적이면서도 쉬운 방법인 구간 내 가운데를 기준으로 분할 하는 방식으로 풀이 할 것이다.
가운데를 기준으로 분할하여 풀이 할 때 아래 4가지 과정만 유의하여 작성하면 된다. (구간 범위 [lo : hi])
1. 가운데 위치를 구한다. ( mid = (lo + hi) / 2 )
2. 가운데 위치를 기준으로 분할하여 왼쪽 구간의 넓이([lo : mid])와 오른쪽 구간의 넓이([mid : hi])를 구한다.
3. 왼쪽과 오른쪽 중 큰 넓이를 변수에 저장한다.
4. 변수에 저장된 넓이와 두 구간을 합친 구간([lo : hi])의 가장 큰 넓이를 구해 두 개 중 가장 큰 넓이를 반환한다.
일단, 1~3번 과정은 쉽게 구현이 가능 할 것이다.
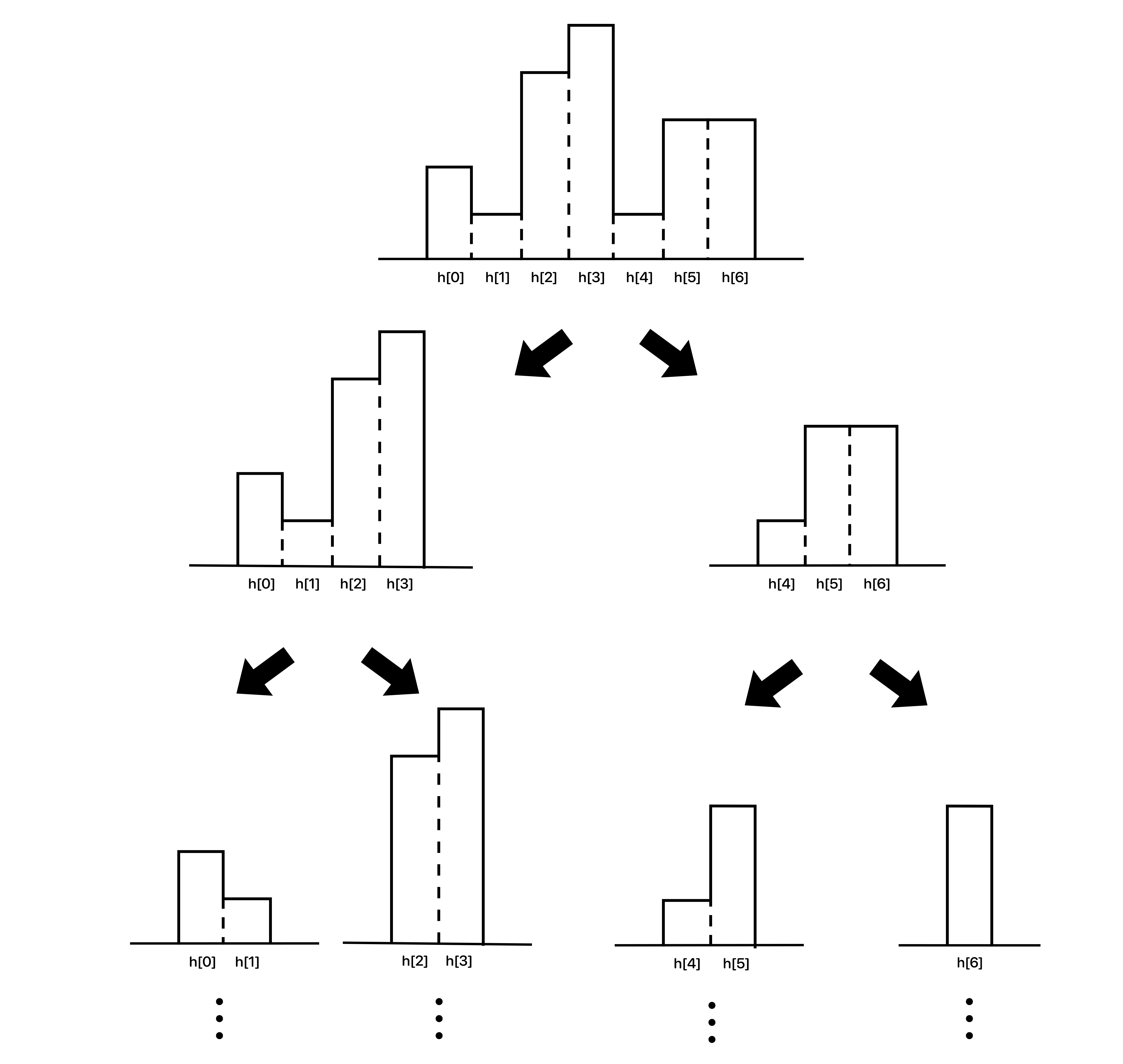
위와 같이 가운데 index를 기준으로 왼쪽과 오른쪽으로 분할 정복하여 막대의 넓이가 1 일 때 까지 재귀 과정을 거친다.
1~3번 과정을 코드로 보자면 다음과 같다.
public static long getArea(int lo, int hi) {
// 막대 폭(넓이)이 1일경우 높이가 넓이가 되므로 바로 반환
if(lo == hi) {
return histogram[lo];
}
// [1번 과정]
int mid = (lo + hi) / 2; // 중간지점
/*
* [2번 과정]
* mid를 기점으로 양쪽으로 나누어 양쪽 구간 중 큰 넓이를 저장
* 왼쪽 부분 : lo ~ mid
* 오른쪽 부분 : mid + 1 ~ hi
*/
long leftArea = getArea(lo, mid);
long rightArea = getArea(mid + 1, hi);
// [3번 과정]
long max = Math.max(leftArea, rightArea);
/*
* 4번 과정(lo~hi 구간의 최대 넓이)을 구현해야함
*/
return max;
}
(참고로 단일 막대의 최대 높이는 10억까지 주어지므로 넓이를 구할 경우 int형 범위를 충분히 넘길 수 있는 값이라 넓이 변수는 모두 long으로 써주도록 한다.)
문제는 4번 과정이다.
왜 두 구간을 합친 구간에서 한 번 더 넓이를 구해야하는지 궁금할 수도 있다. 이유는 간단하다. 왼쪽 및 오른쪽으로 분할하여 얻어진 최대 넓이가 전체 구간(lo~hi) 내의 최대 넓이라는 보장이 없기 때문이다.
(그러한 이유 때문에 가장 작은 블럭을 기준으로 분할하기도 하는데, 문제는 Quick Sort의 단점과 유사하게 매 번 분할 되는 구간이 가장 왼쪽 혹은 오른쪽에 존재할 경우 결국 O(N2)으로 2개의 반복문으로 풀이하는 brute force와 같은 시간복잡도를 갖는 방식이 되어버린 다는 것이다. 그래서 이를 해결하기 위해 구간 내 최소값을 찾기 위한 세그먼트 트리를 활용하게 되는 것이다.)
단적으로 다음 예를 한 번 보자.
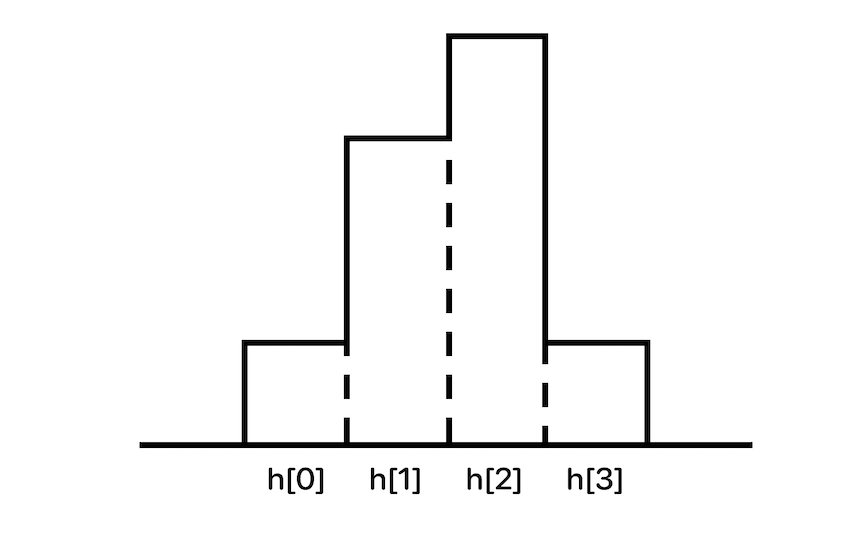
위를 왼쪽과 오른쪽으로 분할 할 경우 각 최대 넓이는 다음과 같을 것이다.
leftArea = 3 (h[0] ~ h[1])
rightArea = 4 (h[2] ~ h[3])
그 중 가장 큰 값을 반환한다고 하면 최대 넓이는 4가 될 것이다.
하지만 우리가 직관적으로 볼 수 있듯이 가장 큰 넓이는 다음과 같다.
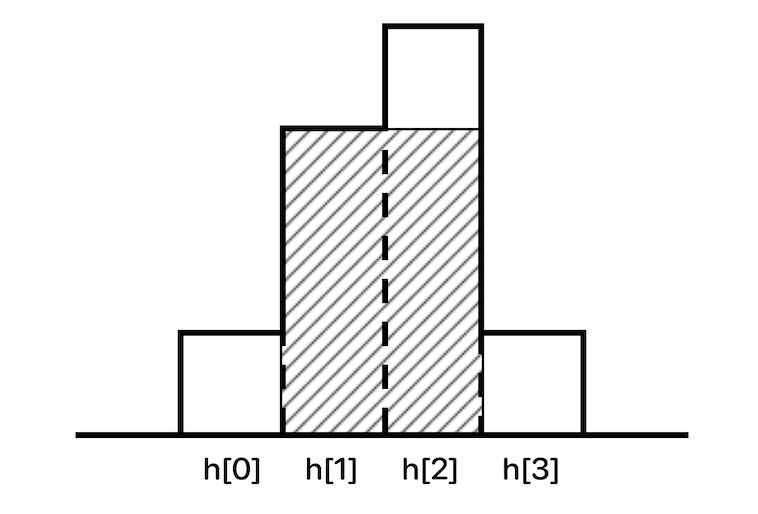
즉 반드시 분할 되어 구해진 넓이가 최대값이라는 보장이 없기 때문에 양쪽 구간을 합친 구간 내에서 mid를 기준으로 양쪽으로 뻗어나가면서 두 구간 사이의 겹친 넓이를 탐색해야 한다.
그러면 어떻게 중간 부분을 탐색해야할까?
일단 넓이가 크다는 것의 의미를 생각해보아야 한다. 넓이가 넓다는 것은 높이가 크거나 폭이 크거나 혹은 둘 다일 경우를 말한다. 즉, 최대한 높이가 높으면서 폭이 큰 쪽으로 탐색해야한다는 의미다.
맨 처음 문제에서 예시로 나온 히스토그램을 기준으로 보자.
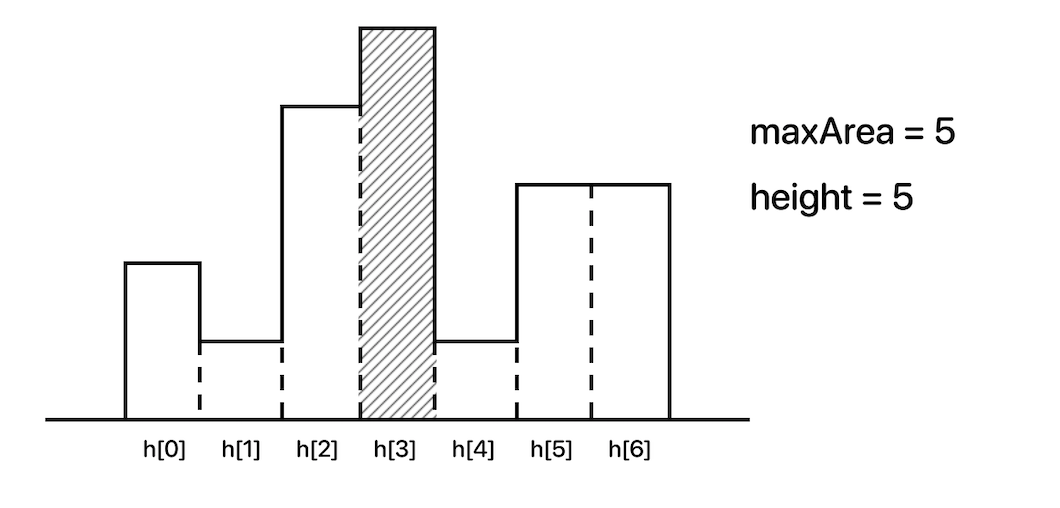
위에 주어진 히스토그램 구간에서 left구간(h[0] ~ h[3])과 right구간(h[4] ~ h[6])으로 나누어 탐색을 한 후라고 가정하자.
그 다음 중간 넓이를 구하기 위해 가운데는 (0 + 6) / 2 = 3 으로 h[3]이 될 것이다. 그리고 맨 처음 h[3]의 넓이는 5일 것이다.
그리고 이제 넓혀가면서 중간 넓이 중 최대 넓이를 찾아야 하는데, 앞서 말했듯 양쪽으로 넓혀가면서 탐색한다고 했다.
그럼 일단, 왼쪽과 오른쪽 중 여러분이 보기에는 어느쪽으로 넓히는게 좋은가? 당연 높이가 높은 쪽으로 확장하는 것이 좋을 것이다.
즉, h[2] 와 h[4] 중 높이가 큰 쪽으로 탐색해보는 것이다. 만약 작은쪽으로 탐색하게 되면 당연하지만 최대 넓이를 찾을 수 없다.
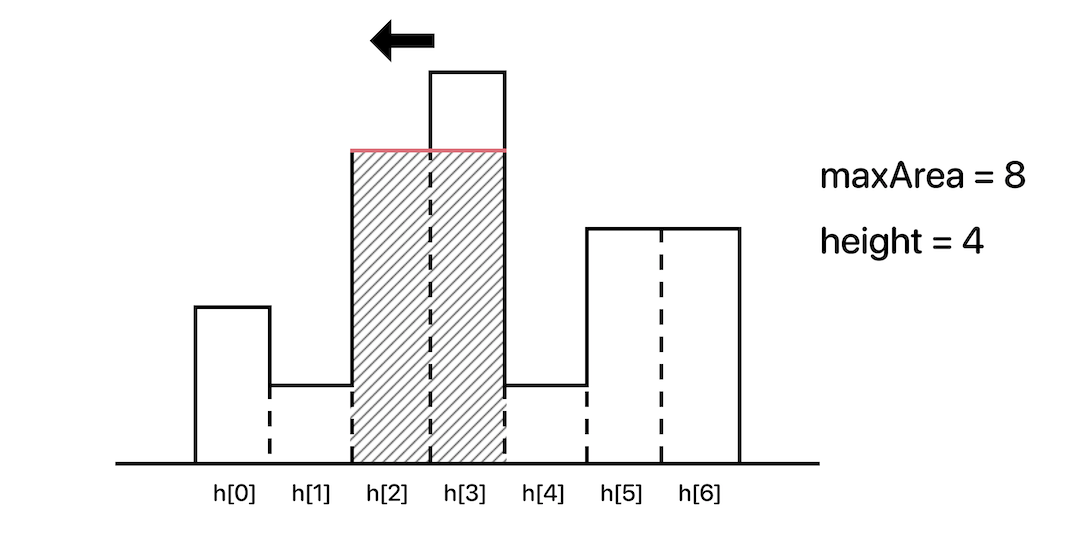
여기서 주의 할 점이 있다.
양쪽의 막대 중 높이가 높을쪽을 택하되, 기존의 높이(height)와 새로 탐색한 막대의 높이 중 작은 것으로 갱신해야한다.
만약 기존의 height(=5)와 새로 탐색한 막대의 height(=4) 중 높은 것을 선택하게 되어버리면 height는 그대로 5일 것이고, 그러면 잘못 된 넓이인 maxArea = 10이 되어버릴 것이다.
즉, 우리는 세 가지의 과정만 유의하면서 처리해주면 된다.
1. 양쪽 다음 인덱스 중 높이가 큰 쪽으로 확장(padding)한다.
2. 갱신되는 높이는 기존의 높이와 확장 한 막대의 높이 중 작은 것을 선택한다.
3. 기존의 넓이와 확장한 넓이 중 큰 값으로 갱신한다.
위 과정을 연속적으로 보면 다음과 같을 것이다.
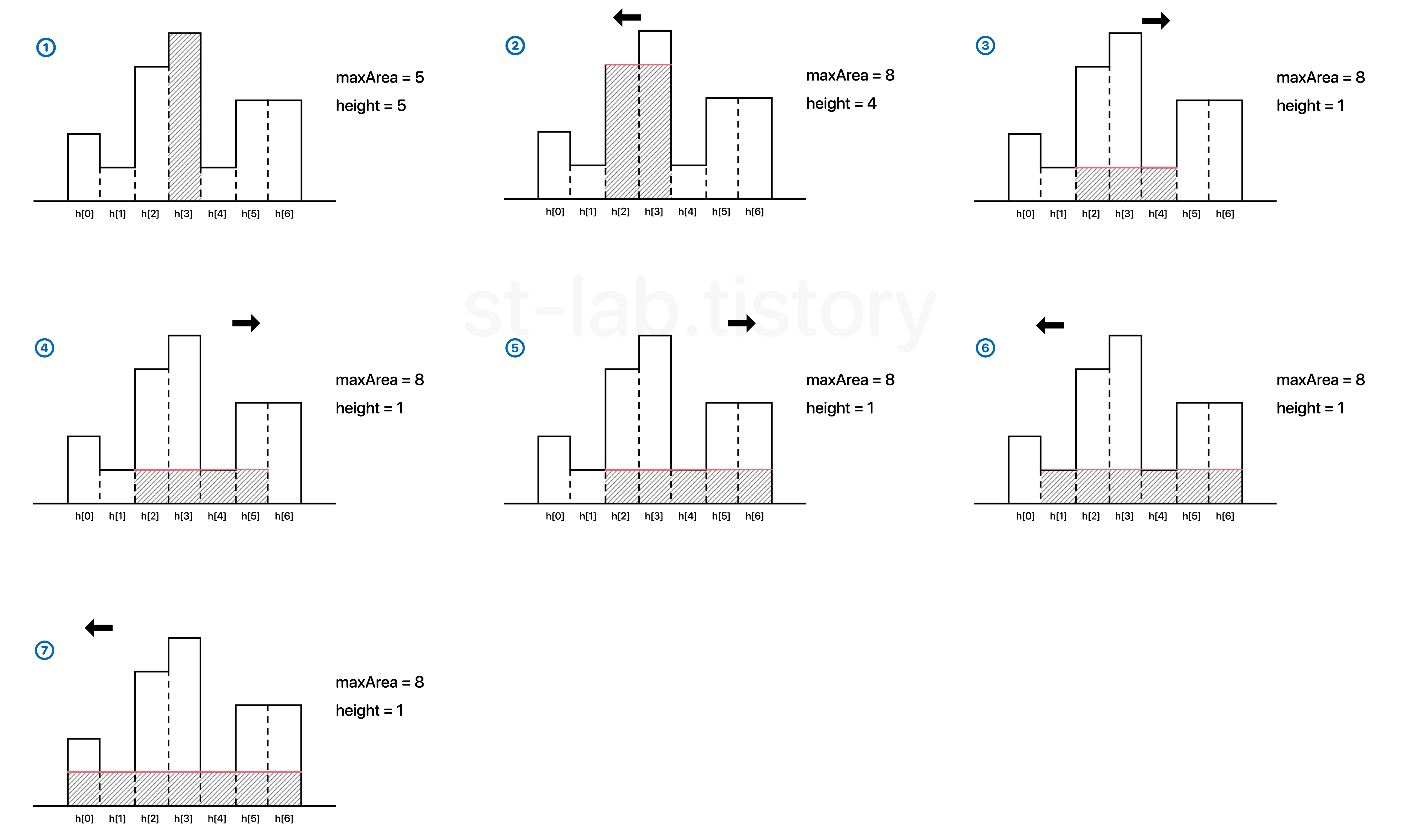
참고로 왼쪽 혹은 오른쪽으로 한 칸씩 탐색하다보면 5번 처럼 어느 한쪽이 먼저 해당 구간의 끝에 닿는 일이 있을 것이다. 그 다음에는 나머지 미탐색 구간을 마저 탐색해주도록 해야한다.
이 것을 코드로 작성하자면 다음과 같다. (메소드를 따로 만들도록 하겠다.)
// 중간지점 영역의 넓이를 구하는 메소드
public static long getMidArea(int lo, int hi, int mid) {
int toLeft = mid; // 중간 지점으로부터 왼쪽으로 갈 변수
int toRight = mid; // 중간 지점으로부터 오른쪽으로 갈 변수
long height = histogram[mid]; // 높이
// [초기 넓이 (구간 폭이 1이므로 넓이는 높이가 면적이 됨)
long maxArea = height;
// 양 끝 범위를 벗어나기 전까지 반복
while(lo < toLeft && toRight < hi) {
/*
* 양쪽 다음칸의 높이 중 높은 값을 선택하되,
* 갱신되는 height는 기존 height보다 작거나 같아야 한다.
*/
if(histogram[toLeft - 1] < histogram[toRight + 1]) {
toRight++;
height = Math.min(height, histogram[toRight]);
}
else {
toLeft--;
height = Math.min(height, histogram[toLeft]);
}
// 최대 넓이 갱신
maxArea = Math.max(maxArea, height * (toRight - toLeft + 1));
}
// 오른쪽 구간을 끝까지 탐색 못했다면 마저 탐색한다.
while(toRight < hi) {
toRight++;
height = Math.min(height, histogram[toRight]);
maxArea = Math.max(maxArea, height * (toRight - toLeft + 1));
}
// 왼쪽 구간을 끝까지 탐색 못했다면 마저 탐색한다.
while(lo < toLeft) {
toLeft--;
height = Math.min(height, histogram[toLeft]);
maxArea = Math.max(maxArea, height * (toRight - toLeft + 1));
}
return maxArea;
}
이렇게 중간의 넓이도 구하는 메소드를 작성해보았다.
이제 앞서 작성한 분할 정복과 위 메소드를 합친다면 다음과 같을 것이다.
[분할정복 방식]
public static long getArea(int lo, int hi) {
// 막대 폭(넓이)이 1일경우 높이가 넓이가 되므로 바로 반환
if(lo == hi) {
return histogram[lo];
}
// [1번 과정]
int mid = (lo + hi) / 2; // 중간지점
/*
* [2번 과정]
* mid를 기점으로 양쪽으로 나누어 양쪽 구간 중 큰 넓이를 저장
* 왼쪽 부분 : lo ~ mid
* 오른쪽 부분 : mid + 1 ~ hi
*/
long leftArea = getArea(lo, mid);
long rightArea = getArea(mid + 1, hi);
// [3번 과정]
long max = Math.max(leftArea, rightArea);
// [4번 과정]
// 양쪽 구간 중 큰 값과 중간 구간을 비교하여 더 큰 넓이로 갱신
max = Math.max(max, getMidArea(lo, hi, mid));
return max;
}
// 중간지점 영역의 넓이를 구하는 메소드
public static long getMidArea(int lo, int hi, int mid) {
int toLeft = mid; // 중간 지점으로부터 왼쪽으로 갈 변수
int toRight = mid; // 중간 지점으로부터 오른쪽으로 갈 변수
long height = histogram[mid]; // 높이
// [초기 넓이 (구간 폭이 1이므로 넓이는 높이가 면적이 됨)
long maxArea = height;
// 양 끝 범위를 벗어나기 전까지 반복
while(lo < toLeft && toRight < hi) {
/*
* 양쪽 다음칸의 높이 중 높은 값을 선택하되,
* 갱신되는 height는 기존 height보다 작거나 같아야 한다.
*/
if(histogram[toLeft - 1] < histogram[toRight + 1]) {
toRight++;
height = Math.min(height, histogram[toRight]);
}
else {
toLeft--;
height = Math.min(height, histogram[toLeft]);
}
// 최대 넓이 갱신
maxArea = Math.max(maxArea, height * (toRight - toLeft + 1));
}
// 오른쪽 구간을 끝까지 탐색 못했다면 마저 탐색한다.
while(toRight < hi) {
toRight++;
height = Math.min(height, histogram[toRight]);
maxArea = Math.max(maxArea, height * (toRight - toLeft + 1));
}
// 왼쪽 구간을 끝까지 탐색 못했다면 마저 탐색한다.
while(lo < toLeft) {
toLeft--;
height = Math.min(height, histogram[toLeft]);
maxArea = Math.max(maxArea, height * (toRight - toLeft + 1));
}
return maxArea;
}
위와 같은 방식으로 분할정복을 할 경우 각 단계를 다음과 같이 표현 할 수 있다.
전체 과정을 T로 둘 때, 우리는 두 개로 분할하여 서브 리스트로 분할하여 풀이되고(2T(N/2)) 그리고 각 재귀 단계마다 중간 면적을 구하게 되는데, 이 때 중간 면적 탐색은 현재 리스트의 길이만큼만 수행하게 된다. (f(N))
즉, T(N) = 2T(N/2) + O(N) 이 된다.
이를 마스터 정리나 귀납법, 재귀 트리 등으로 풀이해보면 O(NlogN)의 시간 복잡도를 갖게 된다.
시간복잡도는 O(NlogN)이 될 것이다.
[스택 자료구조 활용 방식]
이제 분할정복 방식을 알아보았으니, 다른 방식인 스택 자료구조 활용 방식을 알아보도록 하자.
사실 Stack으로 어떻게 이용해야할지는 위 분할정복 방식의 중간지점의 영역 넓이 구하는 원리에서 힌트를 얻을 수 있다.
앞서 높이를 갱신한다고 할 때, '갱신하는 height는 기존의 height보다 작거나 같아야한다' 라고 했다.
이 말을 조금만 생각해보면 다음과 같이 생각 할 수 있다.
'현재 막대가 이전 막대의 높이보다 작을 경우 현재 막대로 가질 수 있는 최대 높이는 현재 높이다.'
이 말은 결국 현재 막대의 높이와 이전 막대의 정보만 알 수 있다면 넓이를 구할 수 있지 않을까? 라는 발상으로 접근하는 것이다.
즉, 이전 막대들의 정보를 기억할 수 있도록 이전 막대들의 높이의 위치를 체인 형식으로 관리를 해주는 것이다.
(histogram을 입력받을 때 배열에 이미 높이를 저장하게 되므로 Stack에 높이 정보를 같이 저장할 필요 없이 index 정보만 담아주면 된다. 이 부분은 구현하면서 설명하도록 하겠다.)
접근 방식은 간단하다. 다음 그림을 한 번 보자.
일단 모든 과정을 한 이미지에 담기 힘드니 스택에 체인을 관리하는 방식부터 보도록 하겠다.
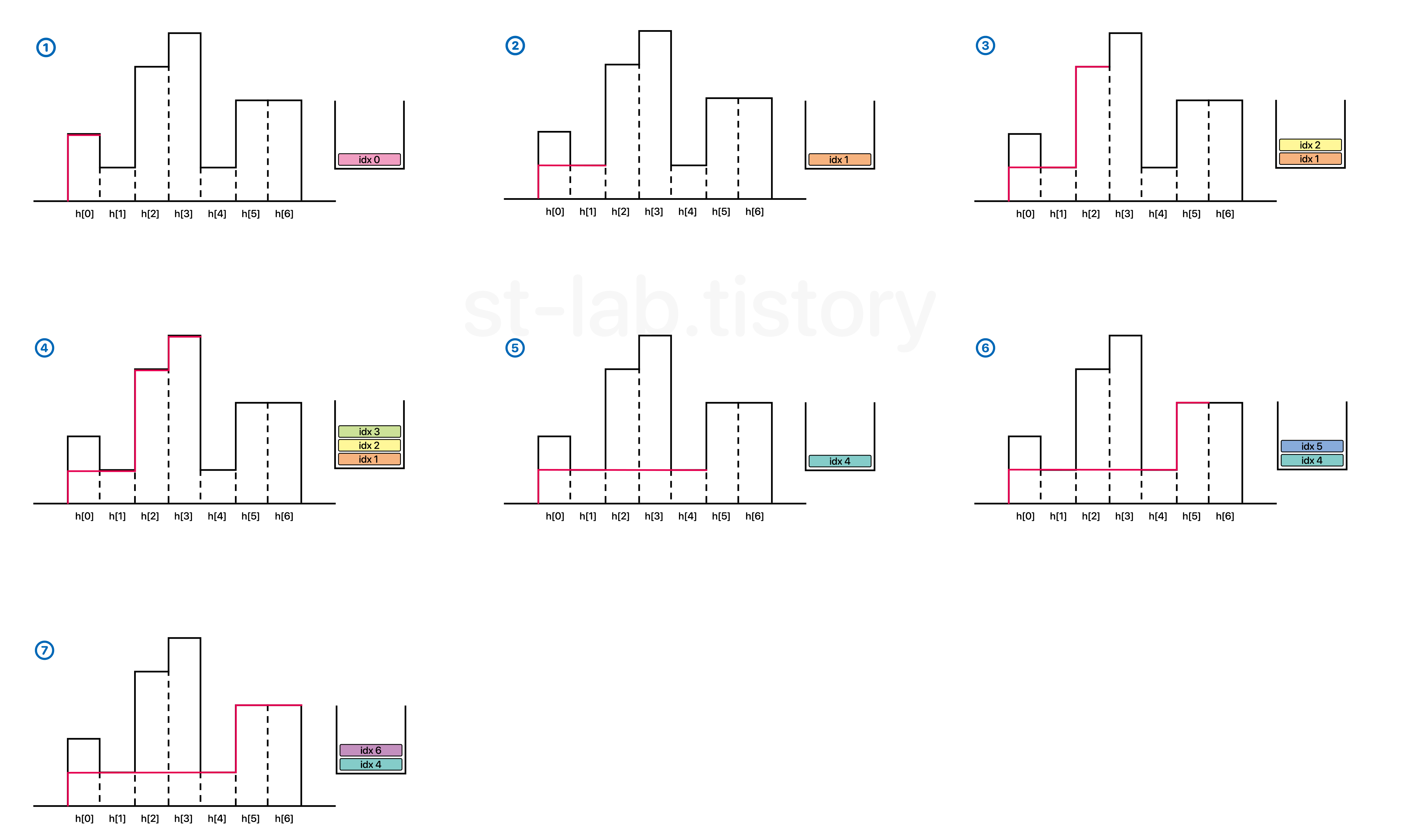
일단, 위 그림을 이해해보자. 규칙을 보면 알겠지만, 한 가지 규칙만 명심하면 된다.
스택의 꼭대기 원소(top)가 가리키는 index의 막대 높이보다 현재 막대의 높이가 작은 경우 현재 막대의 높이보다 크거나 같은 원소는 모두 삭제(pop)하고, 그 다음 현재 막대의 index를 넣는다.(push)
이 것이 이제 스택을 활용하여 체인을 관리하는 것이다.
그럼 넓이는 어디서 구하는 것이냐?
바로 위에서 '현재 막대의 높이보다 크거나 같은 원소는 모두 삭제(pop)' 이 과정에서 삭제하면서 넓이를 구하는 것이다.
예로들어 4번~5번과정을 보자.
스택의 top원소는 idx3이고, index3이 가리키는 막대의 높이는 5다. 그리고 현재 탐색하는 막대는 index 4 막대는 높이가 1이다.
그러면 스택에 높이가 1보다 크거나 같은 원소를 삭제할 것이다. 이 때, 차례대로 pop하면서 원소를 삭제하는 것이다. 이미지로 본다면 다음과 같다.
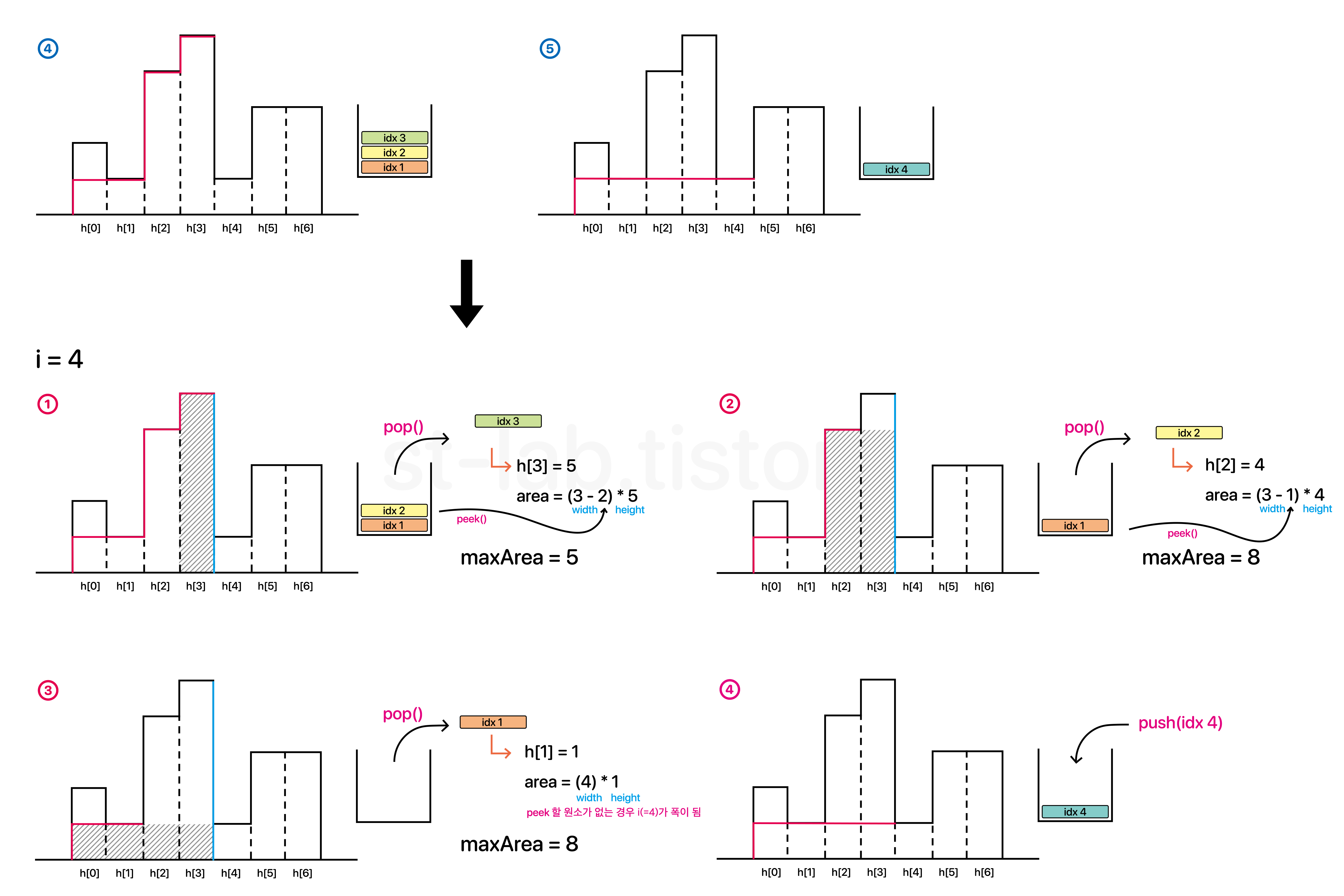
위와 같이 i=4 번째로 탐색 할 때, 4번 막대인 h[4]보다 크거나 같은 원소들을 pop하면서 pop한 원소가 가리키는 막대의 높이를 얻어낼 수 있고, 폭의 경우 (i-1)인 3에서 그 다음의 체인까지의 거리를 빼주어 구할 수 있다.
예로들어 idx 3이 pop 될 경우 다음으로 pop될 원소의 막대는 반드시 idx 3보다 높이가 작은 막대이기 때문에 (i - 1)으로부터 다음으로 pop되는 idx 2 막대와의 거리(width) 는 (i - 1) - 2 가 되고, i는 4였으므로 4 - 1 - 2 = 1인 width를 갖는다.
이를 통해 면적을 계산한 후, maxArea에 최댓값을 갱신시켜주는 방식으로 하면 된다.
이런 방식으로 매 번 pop 할 때마다 위 과정을 거쳐주면 된다.
코드로 보면 다음과 같다.
[스택 활용 방식]
public static long getArea(int len) {
Stack<Integer> stack = new Stack<Integer>();
long maxArea = 0;
for(int i = 0; i < len; i++) {
/*
* 이전 체인의 높이보다 현재 히스토그램 높이가 작거나 같을경우
* i번째 막대보다 작은 이전 체인들을 pop하면서 최대 넓이를 구해준다.
*
*/
while((!stack.isEmpty()) && histogram[stack.peek()] >= histogram[i]) {
int height = histogram[stack.pop()]; // 이전 체인의 높이
/*
* pop한 뒤 그 다음의 이전체인이 만약 없다면 0번째 index 부터 (i-1)번째 인덱스까지가
* 유일한 폭이 된다. (폭은 i가 됨)
* 반면 스택이 비어있지 않다면 이는 pop한 높이보다 더 작은 높이를 갖는
* 체인이 들어있다는 것이므로 (i-1)번째 index에서 그 다음 이전 체인의 index를
* 빼준 것이 폭이 된다.
*/
long width = stack.isEmpty() ? i : i - 1 - stack.peek();
maxArea = Math.max(maxArea, height * width); // 최대 넓이 값 갱신
}
/*
* 위 과정이 끝나면 스택에 저장되어있는 체인은 모두 i보다 작거나 같은
* 체인들 뿐이므로 i번째 index를 넣어준다.
*/
stack.push(i);
}
// 위 과정이 끝나고 Stack에 남아있는 체인들이 존재할 수 있으므로 나머지도 위와같은 과정을 거친다.
while(!stack.isEmpty()) {
int height = histogram[stack.pop()];
/*
* 만약 pop하고 난 뒤 스택이 비어있다면 이는 남아있는 체인이 없다는 뜻이고
* 고로 0 ~ (len - 1) 까지인 전체 폭이 width가 되는 것이다.
*/
long width = stack.isEmpty() ? len: len - 1 - stack.peek();
maxArea = Math.max(maxArea, width * height);
}
return maxArea;
}
이 때 주의 할 점은 주석으로도 달아놓았지만, 결국 순회가 다 끝나면 결국 스택에 잔여 데이터들이 존재할 수 밖에 없다. 그러므로 반드시 나머지 스택에 남겨져 있는 원소들에 대해서도 pop과정을 똑같이 거치면서 넓이를 계산해주면 된다.
스택 자료구조를 활용하면 위 코드를 보면 알겠지만, 원소들을 한 번만 순회하기 때문에 시간 복잡도는 O(N)인 것을 볼 수 있다.
이렇게 두 방식을 설명했으니, 이제 main 함수를 구현하여 테스트케이스만큼 반복해주면 된다.
- 3가지 방법을 사용하여 풀이한다.
이 번 포스팅의 경우 2가지 방식의 알고리즘을 보여주었다. 또한 자바에서 제공하는 Stack 클래스를 이용할 수도 있겠지만, 직접 Stack처럼 기능을 하도록 구현 할 수도 있기 때문에 입출력에 대해서는 따로 분류하여 테스트하지 않고 모두 BufferedReader와 StringBuilder을 사용하도록 하겠다.
쉽게말해 다음 3가지 방식을 테스트 해보도록 하겠다.
1. 분할정복
2. Stack 클래스 활용
3. Stack 직접 구현
- 풀이
- 방법 1 : [분할정복]
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static int[] histogram;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
StringBuilder sb = new StringBuilder();
int N;
while(true) {
st = new StringTokenizer(br.readLine(), " ");
N = Integer.parseInt(st.nextToken());
if(N == 0) {
break;
}
histogram = new int[N];
for(int i = 0; i < N; i++) {
histogram[i] = Integer.parseInt(st.nextToken());
}
sb.append(getArea(0, N - 1)).append('\n');
histogram = null;
}
System.out.println(sb);
}
public static long getArea(int lo, int hi) {
// 막대 폭이 1일경우
if(lo == hi) {
return histogram[lo];
}
// [1번 과정]
int mid = (lo + hi) / 2; // 중간지점
/*
* [2번 과정]
* mid를 기점으로 양쪽으로 나누어 양쪽 구간 중 큰 넓이를 저장
* 왼쪽 부분 : lo ~ mid
* 오른쪽 부분 : mid + 1 ~ hi
*/
long leftArea = getArea(lo, mid);
long rightArea = getArea(mid + 1, hi);
// [3번 과정]
long max = Math.max(leftArea, rightArea);
// 양쪽 구간 중 큰 값과 중간 구간을 비교하여 더 큰 넓이로 갱신
max = Math.max(max, getMidArea(lo, hi, mid));
return max;
}
// 중간지점 영역의 넓이를 구하는 메소드
public static long getMidArea(int lo, int hi, int mid) {
int toLeft = mid; // 중간 지점으로부터 왼쪽으로 갈 변수
int toRight = mid; // 중간 지점으로부터 오른쪽으로 갈 변수
long height = histogram[mid]; // 높이
// [초기 넓이 (구간 폭이 1이므로 넓이는 높이가 면적이 됨)
long maxArea = height;
// 양 끝 범위를 벗어나기 전까지 반복
while(lo < toLeft && toRight < hi) {
/*
* 양쪽 다음칸의 높이 중 높은 값을 선택하되,
* 갱신되는 height는 기존 height보다 작거나 같아야 한다.
*/
if(histogram[toLeft - 1] < histogram[toRight + 1]) {
toRight++;
height = Math.min(height, histogram[toRight]);
}
else {
toLeft--;
height = Math.min(height, histogram[toLeft]);
}
// 최대 넓이 갱신
maxArea = Math.max(maxArea, height * (toRight - toLeft + 1));
}
// 오른쪽 구간을 끝까지 탐색 못했다면 마저 탐색한다.
while(toRight < hi) {
toRight++;
height = Math.min(height, histogram[toRight]);
maxArea = Math.max(maxArea, height * (toRight - toLeft + 1));
}
// 왼쪽 구간을 끝까지 탐색 못했다면 마저 탐색한다.
while(lo < toLeft) {
toLeft--;
height = Math.min(height, histogram[toLeft]);
maxArea = Math.max(maxArea, height * (toRight - toLeft + 1));
}
return maxArea;
}
}
가장 기본적인 분할정복 풀이 방식이라 할 수 있겠다.
사실 분할정복 방식도 워낙 다양하지만, 다 다루기에는 너무 글이 방대해져 못다룬게 아쉽기도 하다만, 다른 블로거들도 자세히 잘 다루고 있으니 다른 블로그 글들을 찾아보는 것을 권한다.
분할 기준을 달리할 뿐, 크게 구조를 벗어나지는 않는지라 쉽게 이해하실 수 있을 것이다.
- 방법 2 : [Stack 클래스 활용]
Stack 자료구조를 활용하여 풀이하는 방법이다. main 메소드 빼고는 나머지는 위 알고리즘 설명에서 풀이했던 방식을 그대로 차용했으므로 그리 어렵지 않게 이해 할 수 있을 것이다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
import java.util.Stack;
public class Main {
public static int[] histogram;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
StringBuilder sb = new StringBuilder();
int N;
while(true) {
st = new StringTokenizer(br.readLine(), " ");
N = Integer.parseInt(st.nextToken());
if(N == 0) {
break;
}
histogram = new int[N];
for(int i = 0; i < N; i++) {
histogram[i] = Integer.parseInt(st.nextToken());
}
sb.append(getArea(N)).append('\n');
histogram = null;
}
System.out.println(sb);
}
public static long getArea(int len) {
Stack<Integer> stack = new Stack<Integer>();
long maxArea = 0;
for(int i = 0; i < len; i++) {
/*
* 이전 체인의 높이보다 현재 히스토그램 높이가 작거나 같을경우
* i번째 막대보다 작은 이전 체인들을 pop하면서 최대 넓이를 구해준다.
*
*/
while((!stack.isEmpty()) && histogram[stack.peek()] >= histogram[i]) {
int height = histogram[stack.pop()]; // 이전 체인의 높이
/*
* pop한 뒤 그 다음의 이전체인이 만약 없다면 0번째 index 부터 (i-1)번째 인덱스까지가
* 유일한 폭이 된다. (폭은 i가 됨)
* 반면 스택이 비어있지 않다면 이는 pop한 높이보다 더 작은 높이를 갖는
* 체인이 들어있다는 것이므로 (i-1)번째 index에서 그 다음 이전 체인의 index를
* 빼준 것이 폭이 된다.
*/
long width = stack.isEmpty() ? i : i - 1 - stack.peek();
maxArea = Math.max(maxArea, height * width); // 최대 넓이 값 갱신
}
/*
* 위 과정이 끝나면 스택에 저장되어있는 체인은 모두 i보다 작거나 같은
* 체인들 뿐이므로 i번째 index를 넣어준다.
*/
stack.push(i);
}
// 위 과정이 끝나고 Stack에 남아있는 체인들이 존재할 수 있으므로 나머지도 위와같은 과정을 거친다.
while(!stack.isEmpty()) {
int height = histogram[stack.pop()];
/*
* 만약 pop하고 난 뒤 스택이 비어있다면 이는 남아있는 체인이 없다는 뜻이고
* 고로 0 ~ (len - 1) 까지인 전체 폭이 width가 되는 것이다.
*/
long width = stack.isEmpty() ? len: len - 1 - stack.peek();
maxArea = Math.max(maxArea, width * height);
}
return maxArea;
}
}
크게 어려울 것은 없을 것이다. 이번 문제는 중복을 고려하지 않아도 되니 오히려 쉬웠을 수도 있다.
- 방법 3 : [Stack 직접 구현]
Stack 자료구조대신 배열을 하나 선언하여 이를 스택처럼 활용하여 풀이하는 방법이다. 기본적으로 자바에서 제공되는 자료구조는 여러 방면에서 활용 할 수 있도록 여러 Exception 처리와 구조 자체가 복잡하여 단순 배열로 풀이하는 것 보다는 무거울 수 밖에 없다.
그러므로 이런 제한 된 상황에 한정하여 알고리즘을 풀이 할 경우 배열을 하나 만들어 Stack처럼 활용하는 것이 좀 더 시간을 줄일 수 있을 것이다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static int[] histogram;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
StringBuilder sb = new StringBuilder();
int N;
while(true) {
st = new StringTokenizer(br.readLine(), " ");
N = Integer.parseInt(st.nextToken());
if(N == 0) {
break;
}
histogram = new int[N];
for(int i = 0; i < N; i++) {
histogram[i] = Integer.parseInt(st.nextToken());
}
sb.append(getArea(N)).append('\n');
histogram = null;
}
System.out.println(sb);
}
public static long getArea(int len) {
int[] stack = new int[len]; // 스택 배열
int sSize = 0; // 요소의 개수(사이즈)
int top = -1; // top을 가리키는 변수
long maxArea = 0;
for(int i = 0; i < len; i++) {
/*
* 이전 체인의 높이보다 현재 히스토그램 높이가 작거나 같을경우
* i번째 막대보다 작은 이전 체인들을 pop하면서 최대 넓이를 구해준다.
*
*/
while(sSize > 0 && histogram[stack[top]] >= histogram[i]) {
int height = histogram[stack[top--]]; // 이전 체인의 높이
sSize--;
/*
* pop한 뒤 그 다음의 이전체인이 만약 없다면 0번째 index 부터 (i-1)번째 인덱스까지가
* 유일한 폭이 된다. (폭은 i가 됨)
* 반면 스택이 비어있지 않다면 이는 pop한 높이보다 더 작은 높이를 갖는
* 체인이 들어있다는 것이므로 (i-1)번째 index에서 그 다음 이전 체인의 index를
* 빼준 것이 폭이 된다.
*/
long width = sSize == 0 ? i : i - 1 - stack[top];
maxArea = Math.max(maxArea, height * width); // 최대 넓이 값 갱신
}
/*
* 위 과정이 끝나면 스택에 저장되어있는 체인은 모두 i보다 작거나 같은
* 체인들 뿐이므로 i번째 index를 넣어준다.
*/
stack[++top] = i;
sSize++;
}
// 위 과정이 끝나고 Stack에 남아있는 체인들이 존재할 수 있으므로 나머지도 위와같은 과정을 거친다.
while(sSize > 0) {
int height = histogram[stack[top--]];
sSize--;
/*
* 만약 pop하고 난 뒤 스택이 비어있다면 이는 남아있는 체인이 없다는 뜻이고
* 고로 0 ~ (len - 1) 까지인 전체 폭이 width가 되는 것이다.
*/
long width = sSize == 0 ? len: len - 1 - stack[top];
maxArea = Math.max(maxArea, width * height);
}
return maxArea;
}
}
(위 방법에서 따로 top원소를 pop할 때 변수를 지우지 않았다. 어차피 top을 통해 index를 활용하고, 만약에 기존에 있던 값에 변수가 push 될 경우 값을 덮어버리면 되기 때문에..)
- 성능

채점 번호 : 30153672 - 방법 3 : 스택 직접 구현
채점 번호 : 30153664 - 방법 2 : 스택 클래스 활용
채점 번호 : 30153660 - 방법 1 : 분할정복
보시다시피 라이브러리를 사용하지 않고 직접 구현한 경우인 1번과 3번을 비교해보면 스택 방식이 더욱 빠른 것을 볼 수 있다. 반면 2번의 경우 자체가 무겁다보니까 아무래도 속도 측면에서는 떨어질 수 밖에 없다. 하지만 알고리즘 분석적으로 보면 스택방식이 분할정복보다 빠른 것은 사실이다.
- 정리
이 번 문제는 조금 어려웠을 것이다. 필자도 처음 풀이 했을 때 분할 정복 파트에 들어가 있어서 일단 분할정복으로 풀이했지만, 필자와는 다른 방식으로 풀이 할 경우(낮은 막대를 기준으로 분할한다거나 등) 보통은 세그먼트 트리로 구간 합을 이용하여 풀이하곤 했다. 왜냐하면 만약 낮은 막대를 기준으로 분할하게 될 경우 정렬된 상태에서는 최악의 경우 O(N2)의 시간복잡도를 갖기 때문이다. 이를 개선하고자 특정 구간 내 정보를 담아서 최악의 경우에도 O(NlogN)으로 풀 수 있도록 하는 것이다.
다만, 이 부분에 대해 다루지 않은 이유가 이후 세그먼트 트리 카테고리가 따로 있기 때문에.. 만약 해당 부분까지 진도가 나간다면 그 때 이 문제를 세그먼트 트리로 푸는 방법을 업데이트 하거나 하겠다.
그리고 Stack을 활용하는 방식의 경우는 문제 자체도 유명하기도 하고, 또한 다양한 풀이 방법 중 Stack을 활용하는 방법이 대표적이기도 하여 이 전에 스택 카테고리도 이미 다루었겠다 해당 방법도 같이 보여주었다.
이 문제가 solved.ac 기준으로 플레티넘 문제인데 아마 처음으로 플레티넘 문제를 다뤄보았을 것이다. 또한 처음 보시는 분들의 경우 어려운 문제였으리라 생각한다.
혹여 어렵거나 이해가 되지 않은 부분, 혹은 잘못 된 부분이 있다면 댓글로 남겨주시길 바란다. 댓글은 언제나 환영한다.
(여담으로 근래 포스팅 업로드가 조금 늦어지고 있는데, 사실 hybrid 정렬 부분을 다루려고 벤치마킹하는 중인데 며칠 째 테스트 중이라(데이터를 너무 많이 넣었다..) 안되겠다싶어 문제를 풀이하고 테스트가 끝나는대로 다루기로 했다. 근데 하필 포토샵을 잘 다루지 못하는데 포토샵 작업이 좀 많은 문제라 시간이 좀 걸렸다. 아무쪼록 조금 더 속도를 내보도록 노력하겠다.)
'JAVA - 백준 [BAEK JOON] > 분할 정복' 카테고리의 다른 글
| [백준] 11444번 : 피보나치 수 6 - JAVA [자바] (11) | 2021.05.27 |
|---|---|
| [백준] 10830번 : 행렬 제곱 - JAVA [자바] (7) | 2021.05.24 |
| [백준] 2740번 : 행렬 곱셈 - JAVA [자바] (7) | 2021.05.05 |
| [백준] 11401번 : 이항 계수 3 - JAVA [자바] (2) | 2021.04.23 |
| [백준] 1629번 : 곱셈 - JAVA [자바] (21) | 2021.04.07 |