[백준] 11444번 : 피보나치 수 6 - JAVA [자바]
https://www.acmicpc.net/problem/11444
11444번: 피보나치 수 6
첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.
www.acmicpc.net
- 문제

- 알고리즘 [접근 방법]
이 번 문제는 단계별로 차근차근 풀었었다면 여러 번에 걸쳐 피보나치 수를 구하는 문제들을 풀어왔기 때문에 그렇게 어렵지는 않았을 것이다.
그동안 풀어왔던 피보나치 수와 관련된 문제들은 다음과 같다.
다만 문제는 똑같더라도 주어지는 입력의 범위는 엄청 다르다.
이 번 문제의 경우 n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이기 때문에 동적계획법으로 풀이하더라도 그동안 풀이해왔던 dp[] 배열을 사용하여 n에 대해 탐색했는지 여부를 사용 할 수 없다. (대신 HashMap같은 자료구조를 활용하여 n은 key값, 그리고 n에대한 피보나치 수를 value로 저장하는 방식으로 활용할 수는 있다.)
그러면 이를 어떻게 풀이해야 할까?
생각보다 효율적이게 풀이 할 수 있는 방법이 있다. 바로 행렬로 만들어서 풀이하는 것이다. 그럼 이렇게 생각할 수 있을 것이다. 음.. 피보나치 수를 어떻게 행렬로 표현한다는거지? 한 번 같이 보도록 하자.
우리는 피보나치 수의 공식을 다음과 같다는 것을 누구나 알 것이다.
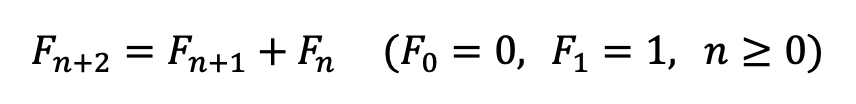
이제 위 방정식을 행렬 꼴로 만들 것이다.
왜 행렬 꼴로 만드는가?
여러분이 대학교에서 공과 계열에 재학중이라면 몇몇 특수 학과를 제외하곤 대개 1학년 혹은 2학년 때 선형대수를 배우거나 배웠을 것이다. 혹은 AI(인공지능), 그래픽스에 관심이 있다면 선형대수(행렬 및 벡터)가 응용되는 분야라는 것은 아실 것이다.
선형방정식을 풀 때 여러 개의 연립방정식이 주어진다면 식을 빼고 더하면서 미지수를 풀어내는 방식으로 많이 풀이했을 것이다. 하지만, 수식이 복잡해지고 많아지면 방정식끼리 더하고 빼고 하는 것은 과정도 복잡해질뿐더러 시간도 오래 걸린다.
하지만, 여러개의 방정식을 하나의 행렬 꼴로 표현하게 될 경우 선형방정식의 해가 존재하는지 없는지 판단을 하기 쉬워질 뿐더러 가우스 소거, 크래머 공식 등 여러 방법에 의해 쉽게 미지수에 대한 답 혹은 일반항을 찾을 수 있다.
즉, 우리가 해야 할 일은 선형방정식을 행렬 꼴(matrix form)로 변환하는 것이다. 좀 더 쉽게 말하자면 위 방정식을 Ax = b 형태의 행렬로 만드는 것이다.
(여담으로 아마 필자가 기억하는 것으로는 지금의 고등학생 및 대학생 절반 이상은 고교과정에서 행렬이 빠진 것으로 알고 있다. 하지만 공학에서는 선형대수는 필수적인 존재라 여러분이 공학계열로 가면 행렬을 한 번쯤은 접할 수 밖에 없을 것이다. 그리고... 요즘 AI가 대세임에도 왜 선형대수의 기초 과정조차 들어가지 않는지 이해는 안가는 건 사실...)
일단 본론으로 돌아가 이 방정식을 행렬로 표현한다면 다음과 같이 표현 할 수 있다.
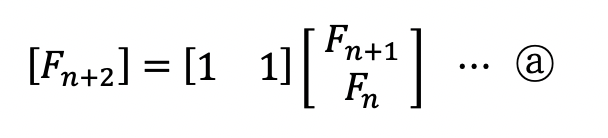
하지만, 이 것만으로는 행렬 연산을 통해 의미를 얻을 수 있는 수식은 아니다. F라는 방정식에 대해 n번째 값을 구하기 위해 Ax=b 꼴로 만들거라고 했다. 그러기 위해 x인 [Fn+1 Fn]T 를 공통으로 둘 수 있는 하나의 간단한 식을 추가하겠다. (T는 행렬의 전치라는 뜻이다. 글로는 세로로 수식을 작성하기 어려워 위와 같이 표현했다. 즉, 1×2 행렬인 식을 위 ⓐ식에서의 가장 마지막에 있는 세로로 된 2×1 행렬을 의미한다.)
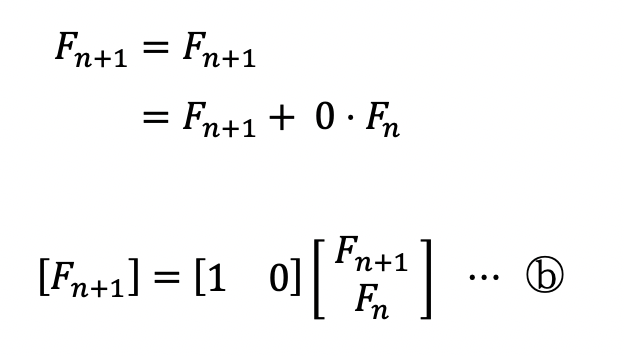
위와 같이 x를 공통인수로 하는 하나의 선형방정식을 얻을 수 있다.
그럼 위 ⓐ식과 ⓑ를 결합해보자.

우리는 이렇게 행렬 꼴로 만들 수 있다.
자 그럼 위 식을 한 번 일반화를 해보자. 우리는 Fn+1 과 Fn을 하나의 열벡터로 볼 수 있다. 이를 un이라고 한다면 Fn+2 와 Fn+1 은 un+1 으로 볼 수 있다. 즉 다음과 같이 표현 할 수 있다.

그러면 이제 u벡터에 대해 한 번 풀어보자.
일단, 우리는 u0에 대한 초기값을 알 수 있다.

그럼 u1 부터 한 번 위 식에 맞게 나열을 해보자.

규칙이 보이지 않는가?
결과적으로 우리는 un = An*u0 으로 A라는 행렬의 n제곱으로 쉽게 구할 수 있다는 것이다. 이를 행렬로 표현하면 다음과 같다.

이렇게 수식을 일반화하여 얻을 수 있다.
그럼 한 번 수식이 맞는지 확인해보자. 만약에 9번째 피보나치 수를 구하고자 한다면 우리는 F9를 얻고 싶은 것이다.
n=8 혹은 9를 대입하면 되므로 한 번 8을 대입해보자.
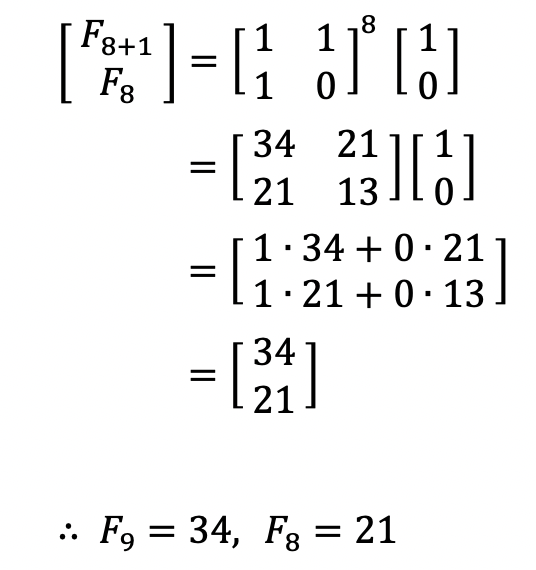
위와 같이 아주 잘 나오는 것을 볼 수 있다.
그러면 마지막으로 위 식을 정말 한 눈에 알아보기 쉽게 더욱 간소화만 하고 마무리 해보자.
우리는 n제곱 할 행렬 A를 얻었다. 여러분들이 만약 몇 가지 케이스들을 대입해보면서 보면 느낄수도 있지만, A12 원소와 A21 원소는 항상 같다는 것을 느낄 수 있다. 그리고 위 n=8 에서 과정을 보면 1 * 34 + 0 * 21 으로 결과적으로 A11 원소가 Fn 원소값이 된다는 것을 확인 할 수 있다.
또한 A12 혹은 A21 과 A22 원소를 더하면 A11 원소를 얻을 수 있다.
그러면 다음과 같이 가정할 수 있지 않을까?

위 가정이 맞는지 증명하는 방법은 매우 간단하다. 행렬 A를 하나는 수로 표현 된 것과 기호로 표현 된 것끼리 곱해보면 될 일이다.

즉, 우리는 행렬 A인 ([1, 1], [1, 0]) 만 갖고도 행렬의 n제곱을 통해 피보나치 수를 얻을 수 있다는 것을 알 수 있다.
그러면 뭔가 감이 올 것이다. 바로 직전 문제에서 풀었던 행렬 제곱 문제를 그대로 응용하면 되는 것이다.
결과적으로 아래 글에서 다룬 알고리즘을 적용하면 된다는 것이다.
(행렬 제곱에 대한 내용은 아래 글에서 다루었으니 따로 설명은 하지 않겠다.)
위 문제를 풀고오지 않았다면 먼저 위 문제부터 풀고오시길 바란다.
또한 피보나치 수의 경우 기하급수적으로 값이 증가하기도 하고, n은 1,000,000,000,000,000,000까지 입력받기 때문에 반드시 long 타입으로 선언해주어야한다.
그리고 모듈러 연산을 해주어야 하니 행렬끼리 곱할 때 각 원소에 1000000007 을 나눈 나머지 값을 저장하면 된다.
- 2가지 방법을 사용하여 풀이한다.
이전 포스팅과 알고리즘상 다를게 크게 없기 때문에 BufferedReader로 통일하여 입력받고, 대신 재귀 방식과 반복문 방식으로 나누어 볼 것이다.
1. 재귀
2. 반복문
- 풀이
- 방법 1 : [재귀]
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
final static long MOD = 1000000007;
public static long[][] origin = {{1, 1} , {1, 0}}; // 초기값을 갖고있는 행렬
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
/*
* n
* | 1 1 | | F(n+1) F(n) |
* A^n = | | = | |
* | 1 0 | | F(n) F(n-1) |
*/
long[][] A = {{1, 1} , {1, 0}};
long N = Long.parseLong(br.readLine());
// Fn 을 구하려면 A행렬을 n-1제곱 한 뒤 반환된 행렬 A11 원소를 출력하면 된다.
System.out.println(pow(A, N - 1)[0][0]);
}
// 행렬 제곱 분할정복 메소드
public static long[][] pow(long[][] A, long exp) {
// 지수가 1 또는 0일 땐 A를 return한다.
if(exp == 1 || exp == 0) {
return A;
}
// 지수를 절반으로 분할하여 재귀호출
long[][] ret = pow(A, exp / 2);
// 하위 재귀에서 얻은 행렬을 제곱해준다.
ret = multiply(ret, ret);
// 만약 지수가 홀수라면 마지막에 A^1 (origin)을 곱해준다.
if(exp % 2 == 1L) {
ret = multiply(ret, origin);
}
return ret;
}
// o1과 o2 행렬을 곱해주는 메소드
public static long[][] multiply(long[][] o1, long[][] o2) {
long[][] ret = new long[2][2];
ret[0][0] = ((o1[0][0] * o2[0][0]) + (o1[0][1] * o2[1][0])) % MOD;
ret[0][1] = ((o1[0][0] * o2[0][1]) + (o1[0][1] * o2[1][1])) % MOD;
ret[1][0] = ((o1[1][0] * o2[0][0]) + (o1[1][1] * o2[1][0])) % MOD;
ret[1][1] = ((o1[1][0] * o2[0][1]) + (o1[1][1] * o2[1][1])) % MOD;
// 반복문으로 작성해주어도 무방함
/*
for (int k = 0; k < 2; k++) {
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
ret[i][j] += o1[i][k] * o2[k][j];
ret[i][j] %= MOD;
}
}
}
*/
return ret;
}
}
가장 기본적인 방법이라 할 수 있겠다.
앞서 말했듯 StringBuilder 가 아니라 System.out.print(arr[i] + " "); 로 하게되면 시간초과가 나므로 주의하자.
StringBuilder 대신 BufferedWriter를 써도 된다.
- 방법 2 : [반복문]
재귀 대신 반복문으로 풀이한 방식이다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
final static long MOD = 1000000007;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
long N = Long.parseLong(br.readLine());
// N이 1이거나 0이라면 N을 출력하고 종료
if(N == 1 || N == 0) {
System.out.println(N);
return;
}
// A^(n-1)의 [0][0] 원소를 구하면 되므로 1을 빼준다.
N--;
long[][] origin = {{1, 1},{1, 0}};
long[][] A = {{1, 0},{0, 1}}; // 초기 값은 단위행렬(I)로 초기화해준다.
/*
* origin 행렬은 이전 loop에서 제곱값을 갖고있는 행렬이고,
* A는 지수가 홀 수 일 때, 이전 loop에서 얻은 제곱 행렬인 origin과
* 현재 A 행렬을 곱해주는 방식으로 간다.
*
* 즉, 재귀 과정을 역순으로 거치면 된다.
*
* ex)
* A^11 과정일 떄,
*
* N = 11 (N % 2 == 1) -> I * A^1 = A^1 (result)
* -> A^1 * A^1 = A^2 (origin)
*
* N = 5 (N % 2 == 1) -> A^1 * A^2 = A^3 (result)
* -> A^2 * A^2 = A^4 (origin)
*
* N = 2 (N % 2 == 0) -> A^4 * A^4 = A^8 (origin)
*
* N = 1 (N % 2 == 1) -> A^3 * A^8 = A^11 (result)
* -> A^8 * A^8 = A^16 (origin)
*/
while(N > 0) {
// 지수가 홀수라면 origin 배열을 한 번 더 곱해준다.
if(N % 2 == 1) { // b % 2 == 1 을 (b & 1L) != 0L 으로도 수정할 수 있다.
A = multiply(A, origin);
}
origin = multiply(origin, origin);
N /= 2;
}
System.out.println(A[0][0]);
}
// o1과 o2 행렬을 곱해주는 메소드
public static long[][] multiply(long[][] o1, long[][] o2) {
long[][] ret = new long[2][2];
ret[0][0] = ((o1[0][0] * o2[0][0]) + (o1[0][1] * o2[1][0])) % MOD;
ret[0][1] = ((o1[0][0] * o2[0][1]) + (o1[0][1] * o2[1][1])) % MOD;
ret[1][0] = ((o1[1][0] * o2[0][0]) + (o1[1][1] * o2[1][0])) % MOD;
ret[1][1] = ((o1[1][0] * o2[0][1]) + (o1[1][1] * o2[1][1])) % MOD;
// 반복문으로 작성해주어도 무방함
/*
for (int k = 0; k < 2; k++) {
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
ret[i][j] += o1[i][k] * o2[k][j];
ret[i][j] %= MOD;
}
}
}
*/
return ret;
}
}
크게 어려울 것은 없을 것이다. 사실 if(N == 1 || N == 0) 은 필요가 없는 문장이긴 하다.
입력은 자연수, 즉 N > 0으로만 주어지기 때문에.. n-1 승을 구하는 과정에서 n-1 이 음수가 될 일도 없고, F1의 경우 1이기 때문에 단위행렬(I)로 초기값을 정해주어도 문제없이 나오긴 한다. 다만 피보나치 수를 구하는 문제인 만큼 F0 = 0인 것도 그냥 확실하게 해두고 싶었다.
- 성능

채점 번호 : 29623231 - 방법 2 : 반복문
채점 번호 : 29623221 - 방법 1 : 재귀
보면 매우 큰 지수임에도 빠르게 구해지는 것을 볼 수 있다.
- 정리
이 번 문제는 아이디어를 떠올리는 것이 조금 어려웠을 수도 있다. 하지만 위와같이 점화식(선형방정식)을 쓸 수 있는 경우 행렬에 대해 깊은 지식을 갖고 있지 않더라도 쉽게 변환할 수 있기 때문에 위와 같이 방정식으로 풀이 되는 문제들은 한 번 쯤은 행렬로 풀이할 수 있는지를 고민해보는 것도 나쁘지는 않다.
만약 어렵거나 이해가 되지 않은 부분이 있다면 언제든 댓글 남겨주시면 최대한 빠르게 답변드리겠다.
'JAVA - 백준 [BAEK JOON] > 분할 정복' 카테고리의 다른 글
| [백준] 6549번 : 히스토그램에서 가장 큰 직사각형 - JAVA [자바] (24) | 2021.06.18 |
|---|---|
| [백준] 10830번 : 행렬 제곱 - JAVA [자바] (8) | 2021.05.24 |
| [백준] 2740번 : 행렬 곱셈 - JAVA [자바] (7) | 2021.05.05 |
| [백준] 11401번 : 이항 계수 3 - JAVA [자바] (2) | 2021.04.23 |
| [백준] 1629번 : 곱셈 - JAVA [자바] (21) | 2021.04.07 |