[백준] 1629번 : 곱셈 - JAVA [자바]
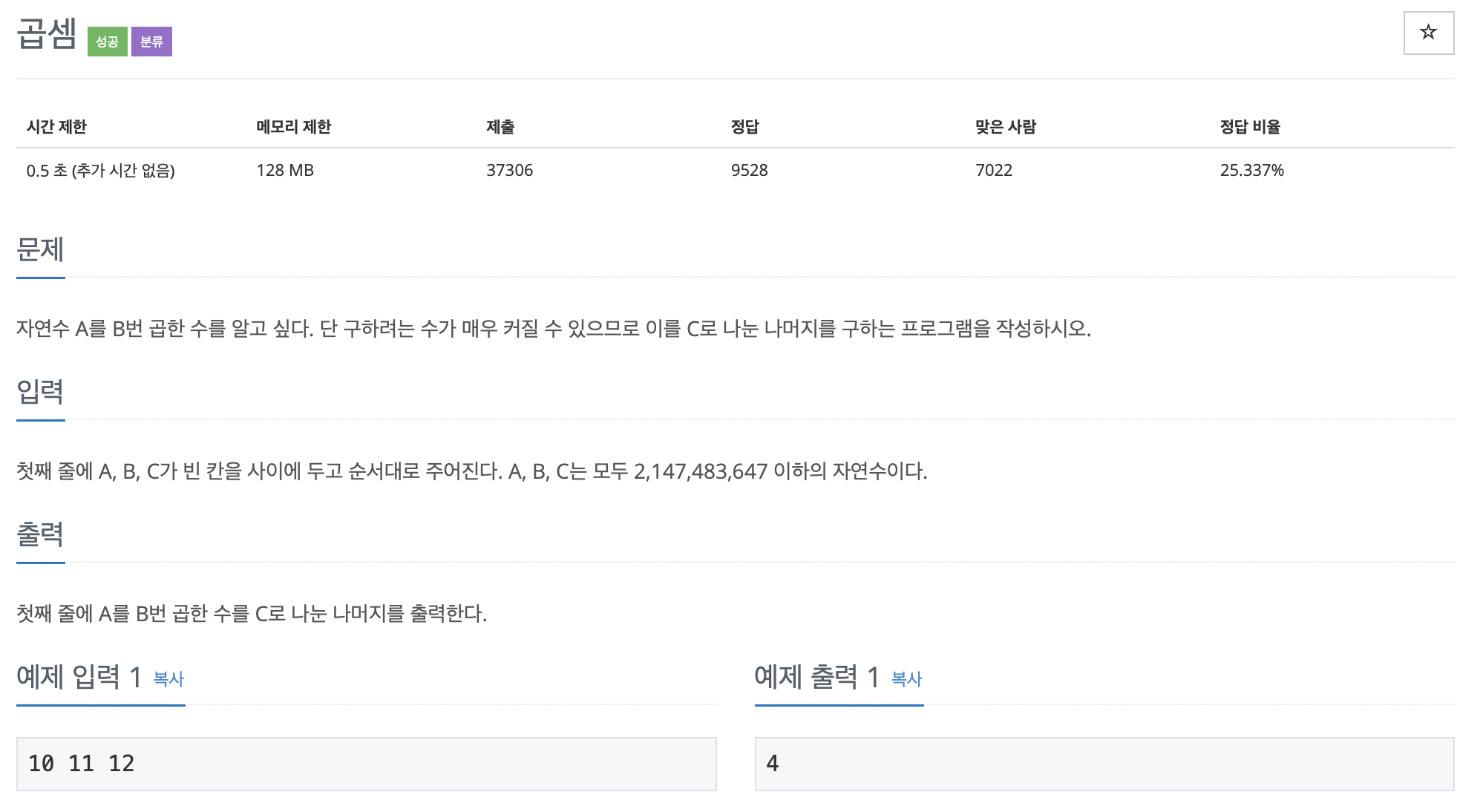
1629번: 곱셈
첫째 줄에 A, B, C가 빈 칸을 사이에 두고 순서대로 주어진다. A, B, C는 모두 2,147,483,647 이하의 자연수이다.
www.acmicpc.net
- 문제
- 알고리즘 [접근 방법]
이 문제는 얼핏보면 B번 거듭제곱 해주면 될 것 같지만... 왜 분할정복 카테고리에 있겠는가.. A, B, C는 각각 최대 2,147,483,647을 갖을 수 있다는 것이고,
2,147,483,647번 거듭제곱 하는 것 부터 많은 수행 과정과, C로 모듈러 연산까지 해주어야 하기 떄문에 시간초과가 날 것이 너무나 뻔하다.
하지만 문제는 그리 어렵지 않다.
우리가 모두가 배웠던 간단한 '지수 법칙'과 '모듈러 성질'만 알고 있으면 된다.
일단 지수법칙 하나.
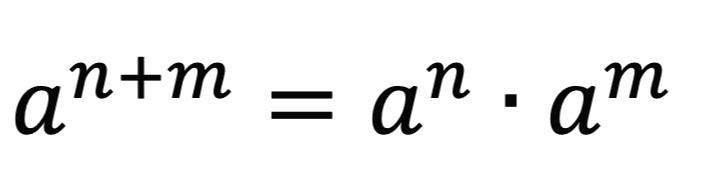
그리고 모듈러 성질 하나.
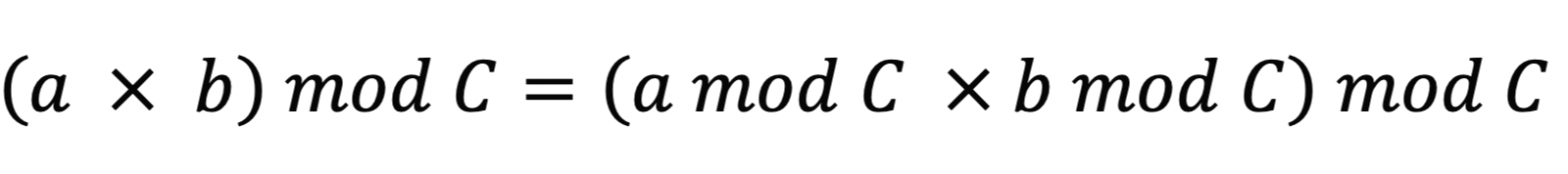
위 모듈러 식을 우리가 사용하는 연산자를 이용하여 표현하면 다음과 같을 것이다.
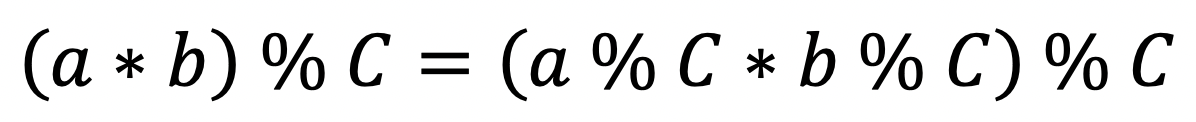
위에 대한 증명은 아래 글을 참고하시길 바란다.
[백준] 10430 번 : 나머지 - JAVA [자바]
https://www.acmicpc.net/problem/10430 10430번: 나머지 첫째 줄에 A, B, C가 순서대로 주어진다. (2 ≤ A, B, C ≤ 10000) www.acmicpc.net 문제 매우 간단한 문제다! ※ 주의할점 입력은 공백단위로 구분 된..
st-lab.tistory.com
그럼 위 예제를 생각해보자. A가 밑(base)이고, B가 지수(exponent)고 C는 결과값에 나눌 값이다. 그리고 각각 10, 11, 12로 입력받았다.
일단, C는 제외하고 거듭제곱 하는 방법부터 고민해보자.
필자가 방금 언급한 지수법칙을 어떻게 이용할 수 있을까?
바로 지수를 반으로 나누는 것이다.
무슨 말이냐면, a8 이 있다면 지수 8를 반으로 나누어 a4 에 대한 값을 한 번 구한 뒤 구한 값을 두 번 곱해주면 된다.
이 때 위 a4 를 구할 때 또한 지수 4를 반으로 나누어 a2 에 대한 값을 한 번 구한뒤 구한 값을 두 번 곱해주면 된다.
이 과정을 지수가 1일 때 까지 반복하는 것이다.
말로 설명하면 어려울 테니 다음 이미지를 보자.
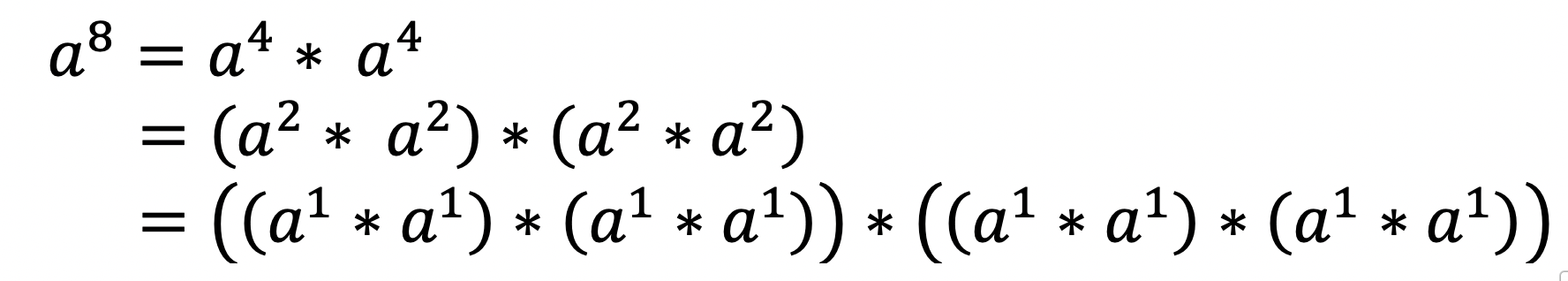
그러면 이런 질문이 있을 것이다.
지수가 홀 수 일 때는 어떻게 해요?
예로들어 a9 같은 경우는 a4 * a4 * a 이렇게 표현하면 되는 것이다. 쉽게 이미지로 보자면 이렇다.

그럼 예제의 A = 10, B = 11 을 위 처럼 적용해보면 이렇다.
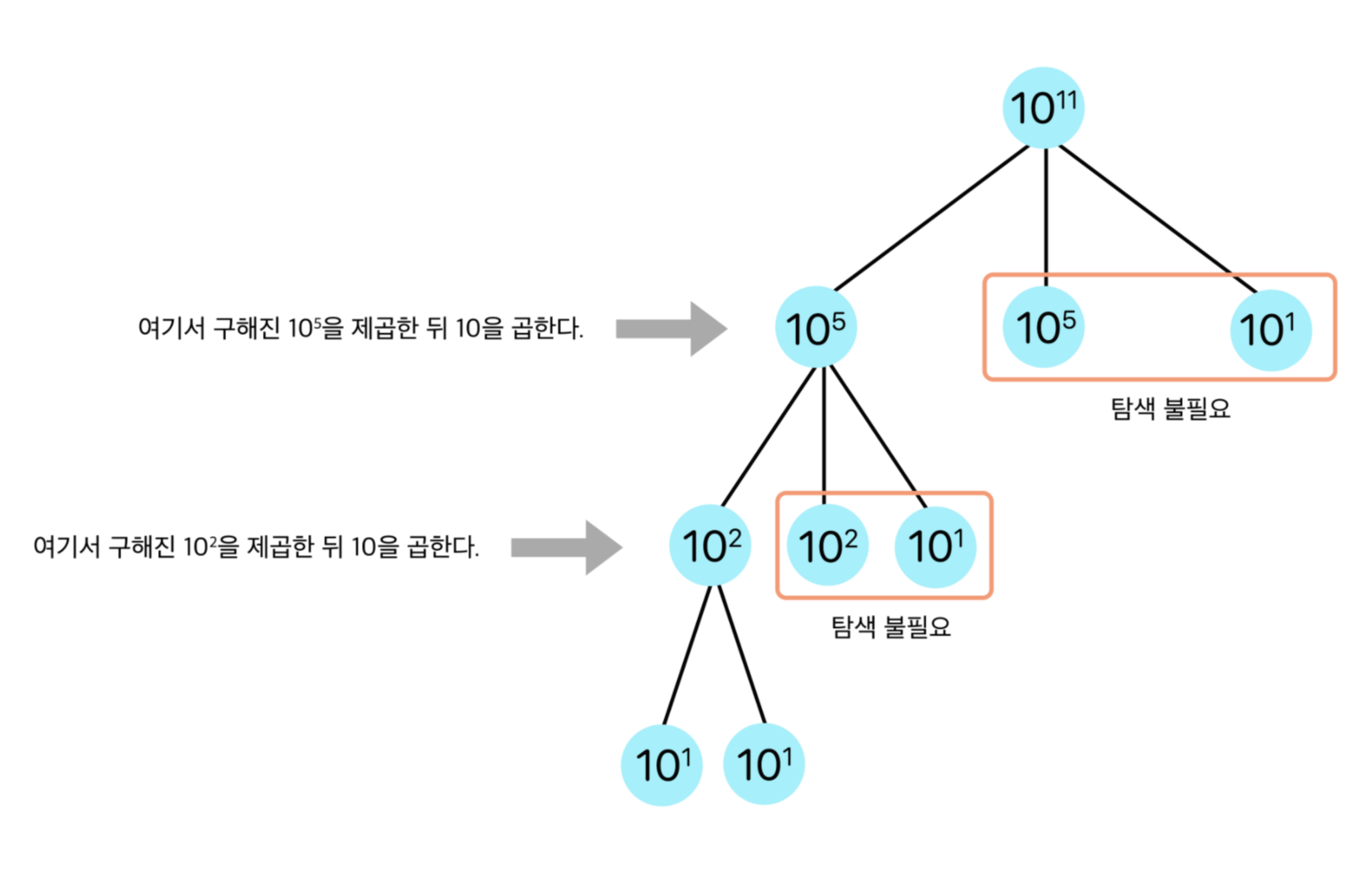
위 과정에서 지수는 절반으로 나누기 때문에 각 레벨에서 나뉜 두 지수를 모두 탐색할 필요없이 한 번만 구하면 된다.
이를 코드로 옮겨보면 이렇게 짤 수 있다.
// A = 밑, exponent = 지수
long pow(long A, long exponent) {
// 지수가 1일 경우 A^1 이므로 A를 그대로 리턴
if(exponent == 1) {
return A;
}
// 지수의 절반에 해당하는 A^(exponent / 2) 을 구한다.
long temp = pow(A, exponent / 2);
/*
* 현재 지수가 홀 수 였다면
* A^(exponent / 2) * A^(exponent / 2) * A 이므로
* A를 한 번 더 곱해주어야 한다.
*
* ex) A^9 = A^4 * A^4 * A
*/
if(exponent % 2 == 1) {
return temp * temp * A;
}
// 그 외에는 짝수이므로 구했던 값을 한 번 더 곱해서 반환한다.
return temp * temp;
}
여기까지는 이해하기 어렵지 않았을 것이다.
이제 두 번째로 생각해야 할 것이 있다. 바로 모듈러 연산이다.
뭐 그냥 return 되는 값에 C로 나눈 나머지값만 붙여주면 되는 거 아닌가? 하고 아래처럼 할 수도 있다.
long pow(long A, long exponent) {
if(exponent == 1) {
return A % C;
}
/*
* 중략
*/
if(exponent % 2 == 1) {
return temp * temp * A % C;
}
return temp * temp % C;
}
위 처럼 하면 '틀린다'
왜냐.. 다음 부분을 한 번 자세히 보자.
if(exponent % 2 == 1) {
return temp * temp * A % C;
}
문제에서 주어지는 각 최댓값은 int형의 max값이다. 즉, 2,147,483,647 (231-1)을 입력받을 수 있다는 뜻이다. 대략 2*109 정도 된다.
long형의 경우 9,223,372,036,854,775,807 (263-1) 이고 대략 9*1018 정도 된다.
예로들어 temp가 2,147,483,647 라면 어떻게 할 것인가.
temp * temp는 long형 안에서 오버플로우 없이(long 타입 범위 안) 가능하다. (231-1) * (231-1) < 263-1 이 식을 만족하기 때문에
temp * temp % C는 가능하다는 뜻이다.
하지만, 밑 또한 2,147,483,647 이라면 어떻게 될까?
(231-1) * (231-1) * (231-1) ≒ 294 로 딱 보더라도 long 형 범위를 넘어간다.
즉, temp * temp * A % C 에서 temp * temp * A 이 부분이 long 범위를 넘어가면서 잘못된 값으로 계산이 되어버린다.
그래서 모듈러 합동 공식을 알고있어야 한다는 점이 이 것 때문이다.
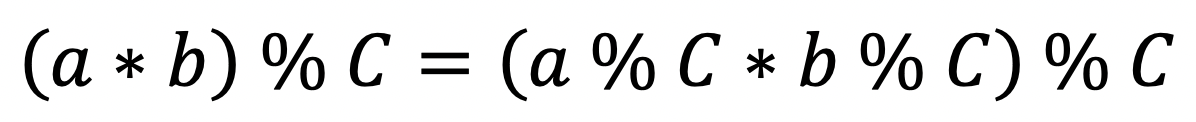
위 식을 다시 보자.
여기서 temp * temp 는 long 형 범위를 넘어가지 않으니 a라고 보고, b를 A라고 생각하면 다음과 같이 변형할 수 있다.
// (a * b) % C = ((a % C)*(b % C)) % C
(temp * temp * A) % C = ((temp * temp % C) * (A % C)) % C
= (((temp * temp % C) % C) * (A % C)) % C // (temp * temp % C) = (temp * temp % C) % C
= ((temp * temp % C) * A) % C
즉, 이 부분만 고려하여 다음과 같이 리턴 값에 모듈러 연산을 해주면 된다.
long pow(long A, long exponent) {
if(exponent == 1) {
return A % C;
}
/*
* 중략
*/
if(exponent % 2 == 1) {
return (temp * temp % C) * A % C;
}
return temp * temp % C;
}
위 설명을 토대로 코드를 작성해주면 된다.
- 2가지 방법을 사용하여 풀이한다.
이전 포스팅과 여타 다를 바 없이 아래와 같이 두 가지 입출력 방법을 통해 성능을 비교해보려 한다.
1. Scanner
2. BufferedReader
- 풀이
- 방법 1 : [Scanner]
import java.util.Scanner;
public class Main {
public static long C;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
long A = in.nextLong();
long B = in.nextLong();
C = in.nextLong();
System.out.println(pow(A, B));
}
// A^exponent
public static long pow(long A, long exponent) {
// 지수가 1일 경우 A^1 이므로 A를 그대로 리턴
if(exponent == 1) {
return A % C;
}
// 지수의 절반에 해당하는 A^(exponent / 2) 을 구한다.
long temp = pow(A, exponent / 2);
/*
* 현재 지수가 홀 수 였다면
* A^(exponent / 2) * A^(exponent / 2) * A 이므로
* A를 한 번 더 곱해주어야 한다.
*
* ex) A^9 = A^4 * A^4 * A
*/
if(exponent % 2 == 1) {
return (temp * temp % C) * A % C;
}
return temp * temp % C;
}
}
가장 기본적인 방법이라 할 수 있겠다.
보면 코드 자체는 그리 길지가 않다. 크게 어려운 것 같지도 않지만, 의외로 모듈러 연산, 연산 범위 체크를 신경써주어야 하기 때문에 조금은 어려웠을 수도 있을 것 같다.
- 방법 2 : [BufferedReader]
입력 방법을 Scanner 대신 BufferedReader 을 사용하여 풀이하는 방법이다. 알고리즘 자체는 같다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static long C;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
long A = Long.parseLong(st.nextToken());
long B = Long.parseLong(st.nextToken());
C = Long.parseLong(st.nextToken());
System.out.println(pow(A, B));
}
// A^exponent
public static long pow(long A, long exponent) {
// 지수가 1일 경우 A^1 이므로 A를 그대로 리턴
if(exponent == 1) {
return A % C;
}
// 지수의 절반에 해당하는 A^(exponent / 2) 을 구한다.
long temp = pow(A, exponent / 2);
/*
* 현재 지수가 홀 수 였다면
* A^(exponent / 2) * A^(exponent / 2) * A 이므로
* A를 한 번 더 곱해주어야 한다.
*
* ex) A^9 = A^4 * A^4 * A
*/
if(exponent % 2 == 1) {
return (temp * temp % C) * A % C;
}
return temp * temp % C;
}
}
크게 어려울 것은 없을 것이다. 이번 문제는 중복을 고려하지 않아도 되니 오히려 쉬웠을 수도 있다.
- 성능

채점 번호 : 28133815 - 방법 2 : BufferedReader
채점 번호 : 28133808 - 방법 1 : Scanner
입력의 경우는 확실히 Scanner 보다는 BufferedReader 가 빠른 걸 볼 수 있다.
- 정리
이 번 문제는 분할정복 개념 자체 접근 방식은 쉬웠으나 연산과정에서 long타입이 넘어가는지를 잘 체크했어야 하는 문제다.
물론 A자체를 곱해주면서 가는 방식으로 풀어도 있지만, 이 방식이 이해하기 가장 빠를 것 같기도 하고 모듈러 연산에 대해 한 번 더 짚고 넘어가자는 마음에 위 방식으로 설명하였다.
혹여 어렵거나 이해가 되지 않은 부분이 있다면 언제든 댓글 남겨주시면 최대한 빠르게 답변드리겠다.
'JAVA - 백준 [BAEK JOON] > 분할 정복' 카테고리의 다른 글
| [백준] 2740번 : 행렬 곱셈 - JAVA [자바] (7) | 2021.05.05 |
|---|---|
| [백준] 11401번 : 이항 계수 3 - JAVA [자바] (2) | 2021.04.23 |
| [백준] 1780번 : 종이의 개수 - JAVA [자바] (4) | 2021.04.05 |
| [백준] 1992번 : 쿼드트리 - JAVA[자바] (0) | 2021.03.23 |
| [백준] 2630번 : 색종이 만들기 - JAVA [자바] (6) | 2021.03.17 |