[백준] 10430번 : 나머지 - [C++]
https://www.acmicpc.net/problem/10430
10430번: 나머지
첫째 줄에 A, B, C가 순서대로 주어진다. (2 ≤ A, B, C ≤ 10000)
www.acmicpc.net
-
문제
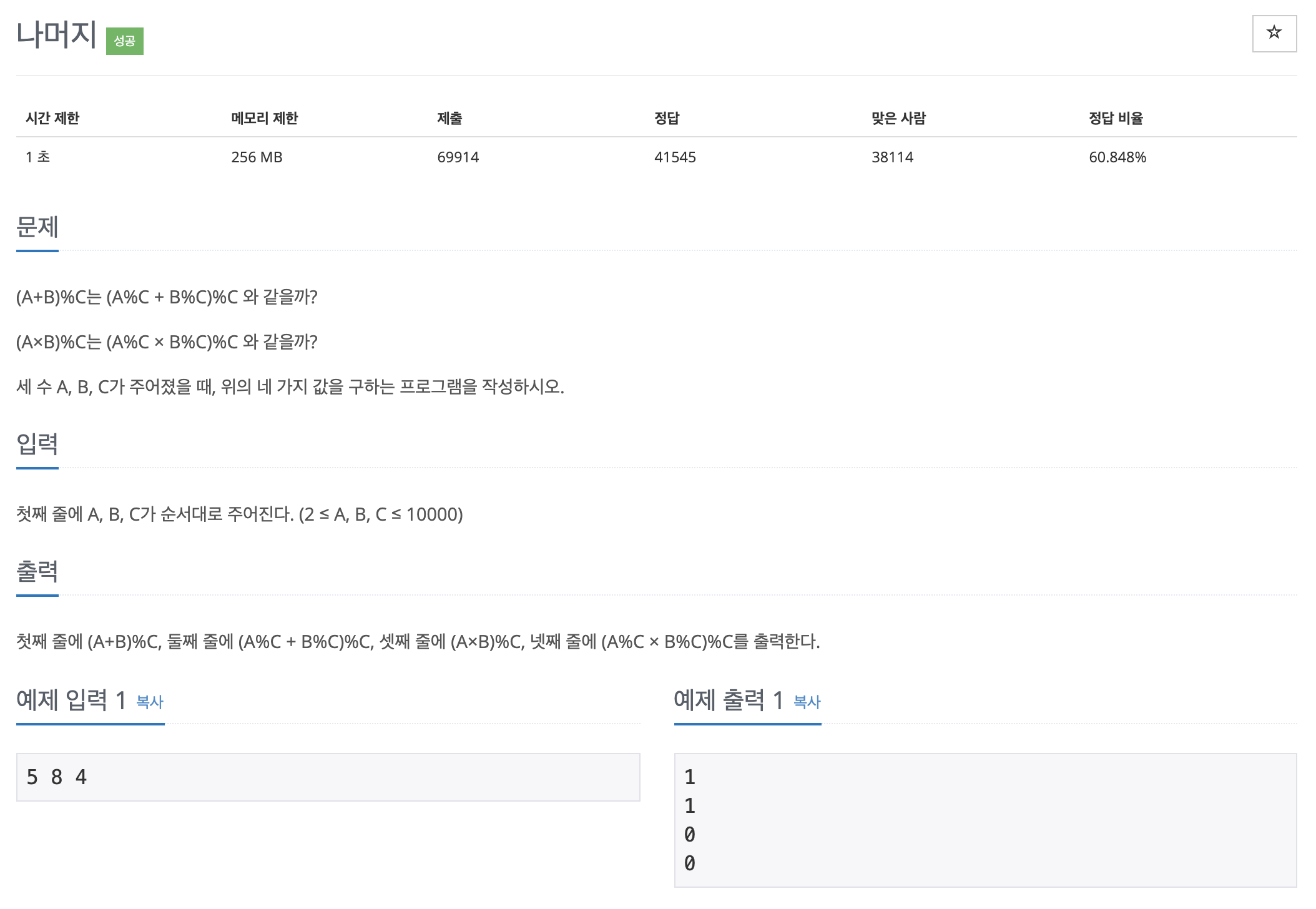
매우 간단한 문제다!
- 풀이하기 전에 ... 모듈러 연산 ( Modular Arithmetic ) 과 증명
직전의 문제에서 필자가 모듈러 연산에 대해 이해를 하면 좋다고 했다.
바로 이러한 문제 때문인데, 위 문제에서 그냥 출력만 하고 땡이지! 라고 하기에는 너무 아까운 문제다. 그러므로 한 번 모듈러 연산에 대한 증명과 성질을 보고가보자.
우리는 프로그래밍에서 대부분 나머지 연산 할 때 %로 표기하며 아래와 같이 표현한다.
17 % 3 = 2이 것을 일반 표기법으로 바꾸면 다음과 같다.
17 mod 3 = 2이제 표현 방법을 알았으니 왜 언급했는지 알려주겠다.
문제에서 총 4개의 케이스가 나왔다.
- (A+B) %C
- (A%C + B%C)%C
- (A*B)%C
- (A%C * B%C)%C
만약 이 문제를 풀어보신 분들을 알겠지만 컴파일 하여 자연수의 어떤 값이던 넣어보면 1번식과 2번식의 값이 같고, 3번식과 4번식의 값이 같다.
이는 모듈러 연산의 대표적 속성 두 가지를 보여주고 있다.
증명 방법을 보고 싶다면 아래 더 보기를 클릭하면 된다.
[증명 1] : (A+B) %C = (A%C + B%C)%C
[증명]
증명 과정 자체는 매우 간단하다.

위 공식대로 풀면 되는데 하나하나 설명해보겠다.
먼저 a 와 b에 대해 c로 나눈 나머지 값을 mod 로 표현하여 정의한다. (이때 T 와 S 는 a 와 b 의 나머지다)
그럼 a와 b에 대하여 식을 변형 할 수 있는데 그게 바로 아래와 같은 것이다.

그럼 저 두 식을 갖고 우리가 증명하려는 식에 대입해보고 식을 정리해보자.

위 식에서 느낌이 오는가?
c = 0 이 아닌 이상 ( i + j )*c 는 0 또는 3의 배수다.
이 말은 i 와 j 의 값에 상관 없이 c의 배수이기 때문에 ( i + j )*c mod c = 0 이다.
즉 나머지 연산에서 ( T + S ) 의 나머지에 대하여 ( i + j )*c 는 위 식의 나머지 값에 대햐여 아무런 영향을 미치지 못한다.
그러므로 다음과 같이 쓸 수 있다.

그리고 T 와 S 는 처음 정의했듯이 각 각 a mod c 와 b mod c 이므로 이들로 교체해주면 우리가 증명하고자 한 공식이 완성된다.

증명 완료
[증명2] : (A*B)%C = (A%C * B%C)%C
[증명2]
이 공식도 1번 증명 방법이랑 유사하다.
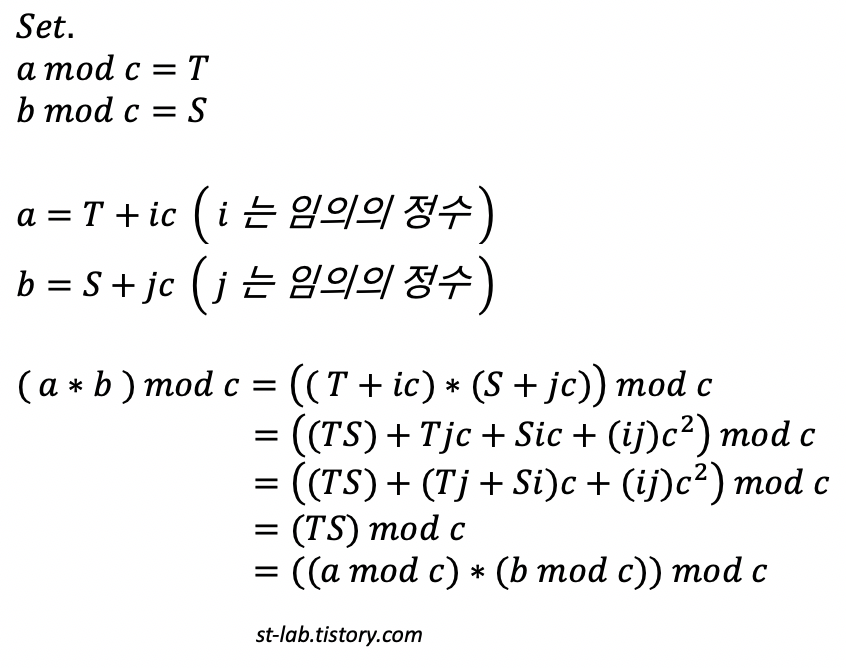
따로 하나하나 설명하지는 않겠다. ( 증명 1 을 이해한다면 이 것도 이해가 될 것이다. )
마찬가지로 곱셈을 풀어준 뒤 c 로 묶인 것들은 나머지 값에 영향을 미치지 못하므로 생략해주면 위 같이 공식이 성립함을 볼 수 있다.
- 2가지 입출력방법을 이용하여 풀이한다.
stdio 로 입출력을 하는 방법과, iostream 입출력을 쓰는 방법. 이렇게 나누어 풀이하도록 하겠다.
1. stdio
2. iostream
- 풀이
- 방법 1 : [stdio]
#include <stdio.h>
int main(int argc, char const *argv[]) {
int A, B, C;
scanf("%d %d %d", &A, &B, &C);
printf("%d\n", (A + B) % C);
printf("%d\n", (A % C + B % C) % C);
printf("%d\n", (A * B) % C);
printf("%d\n", (A % C * B % C) % C);
return 0;
}위에서 주어진 코드를 그대로 출력하면 되는 문제라 그리 어렵진 않을 것이다.
- 방법 2 : [iostream]
iostream을 쓰는 방법이다.
#include <iostream>
using namespace std;
int main(int argc, char const *argv[]) {
int A, B, C;
cin >> A >> B >> C;
cout << (A + B) % C << "\n";
cout << (A % C + B % C) % C << "\n";
cout << (A * B) % C << "\n";
cout << (A % C * B % C) % C << "\n";
return 0;
}
-
성능

위에서 부터 순서대로
채점 번호 : 26745490 - iostream
채점 번호 : 26745485 - stdio
-
정리
문제는 간단했지만 모듈러 연산의 두가지 속성에 대해 알아두었으면 좋겠다 싶어 글이 길어졌다.
나중에 큰 수를 다루면서 '결과 값에 n을 나눈 수를 출력하여라' 같은 문제들을 많이 마주하게 될 것이다. 그럴 때 모듈러 연산에 대한 이해가 없다면 풀이과정을 이해하기 힘들 수 있으니 꼭 익혀두셨으면 한다.
'C++ - 백준 [BAEK JOON] > 입출력과 사칙연산' 카테고리의 다른 글
| [백준] 10926번 : ??! - [C++] (0) | 2022.06.30 |
|---|---|
| [백준] 2588번 : 곱셈 - [C++] (6) | 2021.02.26 |
| [백준] 10869번 : 사칙연산 - [C++] (0) | 2021.02.24 |
| [백준] 1008번 : A/B - [C++] (14) | 2021.02.23 |
| [백준] 10998번 : A×B - [C++] (0) | 2021.02.13 |