[백준] 11051번 : 이항 계수 2 - JAVA [자바]
11051번: 이항 계수 2
첫째 줄에 \(N\)과 \(K\)가 주어진다. (1 ≤ \(N\) ≤ 1,000, 0 ≤ \(K\) ≤ \(N\))
www.acmicpc.net
- 문제

이전의 이항 계수 1 문제와 같은 문제다. 다만 출력할 때 이항 계수 값에 10,007로 나눈 나머지를 출력해야 한다는 점이다.
- 알고리즘 [접근 방법]
일단 이 문제를 풀기 전에 이전에 풀었던 3가지 방식으로 이항 계수를 풀이하는 법을 보고오셨으면 한다.
[백준] 11050번 : 이항 계수 1 - JAVA [자바]
www.acmicpc.net/problem/11050 11050번: 이항 계수 1 첫째 줄에 \(N\)과 \(K\)가 주어진다. (1 ≤ \(N\) ≤ 10, 0 ≤ \(K\) ≤ \(N\)) www.acmicpc.net 문제 알고리즘 [접근 방법] 이항 계수(Binomial coefficie..
st-lab.tistory.com
이 전 문제에서는 입력되는 범위가 1 ≤ N ≤ 10 이였다.
하지만 이번 문제에서는 입력 범위가 다르다. 1 ≤ N ≤ 1000 이다. 그럼 long타입을 쓰면 되나요? 라고 물을 수는 있지만, 결론만 말하면 불가능하다.
참고로 팩토리얼 값으로 보자면 다음과 같다.
12! = 479,001,600 로 int형의 최댓값(2,147,483,647)을 넘어가고 c같이 unsigned int 최댓값(4,294,967,295)도 넘어간다.
20! = 51,090,942,171,709,440,000 으로, long 9,223,372,036,854,775,807 이 넘어간다.
알고리즘 문제를 풀 때 12팩토리얼과 20팩토리얼은 각각 int와 long형이 넘어간다는 것을 알면 좋다.
참고로 다른 팩토리얼 값들도 찾아보고 싶다면 아래 코드를 복사하여 실행해보길 바란다.
import java.math.BigInteger;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.BufferedWriter;
import java.io.OutputStreamWriter;
import java.io.IOException;
public class Factorial_TEST {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
System.out.println("0부터 입력받은 값까지 팩토리얼 값을 출력해줍니다.");
System.out.println("몇 번째까지 팩토리얼 값을 구할지 입력해주세요.\n");
System.out.print("Input N : ");
long j = Long.parseLong(br.readLine().trim());
BigInteger a = BigInteger.ONE;
bw.write("0! = " + a.toString() + "\n");
for(int i = 1; i <= j; i++) {
a = a.multiply(new BigInteger(String.valueOf(i)));
bw.write(i + "! = " + a.toString() + "\n");
}
bw.flush();
bw.close();
}
}
(1000에 대한 팩토리얼 값 보기)
402387260077093773543702433923003985719374864210714632543799910429938512398629020592044208486969404800479988610197196058631666872994808558901323829669944590997424504087073759918823627727188732519779505950995276120874975462497043601418278094646496291056393887437886487337119181045825783647849977012476632889835955735432513185323958463075557409114262417474349347553428646576611667797396668820291207379143853719588249808126867838374559731746136085379534524221586593201928090878297308431392844403281231558611036976801357304216168747609675871348312025478589320767169132448426236131412508780208000261683151027341827977704784635868170164365024153691398281264810213092761244896359928705114964975419909342221566832572080821333186116811553615836546984046708975602900950537616475847728421889679646244945160765353408198901385442487984959953319101723355556602139450399736280750137837615307127761926849034352625200015888535147331611702103968175921510907788019393178114194545257223865541461062892187960223838971476088506276862967146674697562911234082439208160153780889893964518263243671616762179168909779911903754031274622289988005195444414282012187361745992642956581746628302955570299024324153181617210465832036786906117260158783520751516284225540265170483304226143974286933061690897968482590125458327168226458066526769958652682272807075781391858178889652208164348344825993266043367660176999612831860788386150279465955131156552036093988180612138558600301435694527224206344631797460594682573103790084024432438465657245014402821885252470935190620929023136493273497565513958720559654228749774011413346962715422845862377387538230483865688976461927383814900140767310446640259899490222221765904339901886018566526485061799702356193897017860040811889729918311021171229845901641921068884387121855646124960798722908519296819372388642614839657382291123125024186649353143970137428531926649875337218940694281434118520158014123344828015051399694290153483077644569099073152433278288269864602789864321139083506217095002597389863554277196742822248757586765752344220207573630569498825087968928162753848863396909959826280956121450994871701244516461260379029309120889086942028510640182154399457156805941872748998094254742173582401063677404595741785160829230135358081840096996372524230560855903700624271243416909004153690105933983835777939410970027753472000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
그럼 본격적으로 알고리즘을 구성해보자.
앞선 문제(이항 계수 1)에서 3가지 방법에 대한 이항 계수 구하는 방법은 이미 모두 알려주었다. 이 부분은 넘어가고 모듈러 연산에 대해 잠깐 언급하고 바로 코드로 풀이해보도록 하자.
생각보다 모듈러 연산을 잘 활용하는 방법을 모르는 분들이 많다
어렵게 생각할 것 없이 우리가 자바에서 나머지 구할 때 쓰는 % 기호가 바로 모듈러 연산 mod와 같은 의미다.
a mod m = r 표현은 a % m = r 이랑 같은 의미다.
여기서 우리가 생각 할 수 있는게 하나 있다. 바로 'm으로 나눈 나머지 r에 대하여 a는 유일하지 않다' 이다.
이 말이 조금 어렵다면 간단하게 수식으로 다음과 같은 예시가 있겠다.
(34 mod 7) = (27 mod 7) = (62 mod 7) = 6
→ (34 % 7) == (27 % 7) == (62 % 7) == 6
이러한 특징을 거꾸로 뒤집어 보면 다음과 같은 식도 만족한다.
a = km + r (나눈 수 m의 k배수에 r을 더한 값은 a를 만족한다) (k = a div m (몫)이랑 같다.)
위 식을 좀 더 구체적으로 보자면
(34 mod 7 = 6) → (34 = 4 × 7 + 6)
(27 mod 7 = 6) → (27 = 3 × 7 + 6)
등등..
이렇게 m에 대한 배수 + r(나머지 값)으로 a를 구할 수 있다.
이러한 특징 때문에 모듈러 연산에서 다음과 같은 두 식을 만족한다. 이 것은 알고리즘에서 쓸 일이 많을 것이니 꼭 기억해두시길 바란다.
[성질 1]
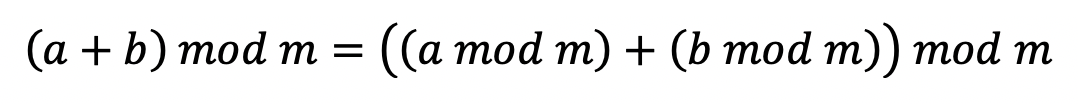
[성질 2]

자세한 증명은 아래 글을 참고하시길 바란다.
이를 프로그래밍 언어로 바꿔보면 아래와 같은 수식일 것이다.
[성질 1]

[성질 2]
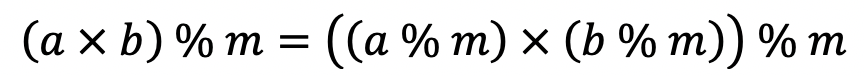
이 두 성질을 잘 이용하면 이항 계수 알고리즘에 다음과 같이 접목하여 구할 수 있다.
*여기서 가장 중요한 점이 있다.
모듈러 연산에서 나눗셈 연산은 '없다'

즉, 앞선 성질 1 이나 성질 2 처럼 분배하여 모듈러 연산을 적용할 수 없다는 뜻이다.
하지만 앞선 문제의 알고리즘 1은 다음과 같은 식을 이용했다.
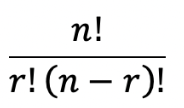
즉, factorial(n) / ( factorial(r) * (factorial(n-r) ) 로 구해서 풀었었다.
그러면 앞선 문제의 알고리즘 1은 못사용하나요? 라고 물을 수 있다. 답을 해드리자면 사용할 수는 있는데, 위와 같은 과정이 아닌 조금 다른 방법으로 찾아야 한다.
방법은 r!(n-r)! 의 역원(역수)을 구하는 것이다. 즉, ( r!(n-r)! )-1 을 구하라는 것. 역원이 구해지면 나눗셈이 아닌 곱셈으로 표현할 수 있기 때문에 위 공식을 만족 할 수 있다. 즉, 아래와 같이 하라는 것이다.

결국에는 역원을 구하는 것이 관건인 문제다.
분모의 값을 지수로 -1 지수로 표현하더라도, 분수는 분수이기 때문이다.
즉, 역원을 통해 분수가 아닌 정수 곱셈으로 표현될 수 있어야 한다.
이를 구하기 위해 사용하는 것이 바로 '페르마의 소정리'다. 즉, 페르마의 소정리를 알아야한다.
ko.wikipedia.org/wiki/페르마의_소정리
페르마의 소정리 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전. 정수론에서, 페르마 소정리(Fermat小定理, 영어: Fermat’s little theorem)는 어떤 수가 소수일 때 간단한 필요 조건에 대한 정리이다. 추상적으로, 소수 크기의 유한체
ko.wikipedia.org
증명까진 시간이 너무 오래 걸리니 일단 공식만 말하자면 이렇다.
페르마의 소정리의 정의는 다음과 같다.

참고로 a ⫮ p 에서 ⫮ 기호는 '나눠지지 않음'이라는 뜻, 즉, a는 p와 배수관계가 아니라는 것이다.
위 식을 보조정리를 이용하여 다음과 같이 표현할 수 있다
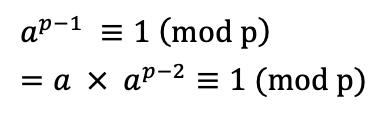
.
보이는가? 결과적으로 ap-2 (mod p)가 a의 역원임을 알 수가 있다.
문제에서 p = 10007 이였고, 지금 우리가 구하고자 하는 역원은 ( r!(n-r)! ) 에 대한 역원 이다. 이 것을 그대로 나누는 수 p도 소수이니 이 두 식을 위 공식에 그대로 적용하자면 이렇다.

결국 최종적으로 우리가 계산하는 식은 다음과 같다.
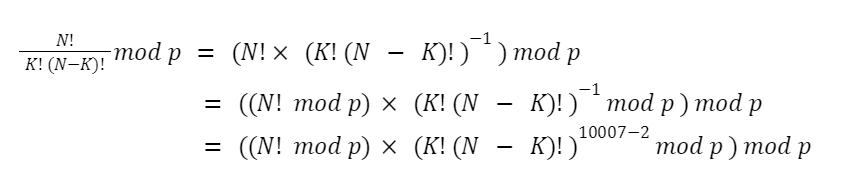
즉 제곱승을 해주는 메소드를 하나 추가하면 알고리즘 1을 이용할 수 있다.
<알고리즘 1>
main {
/*
* n! / ((n-k)! * k!) -> n! * ((n-k)! * k!)^(-1) 으로 변환
* ((n-k)! * k!)^(-1) == ((n-k)! * k!)^(p-2) 동치
* p(=div)가 소수여서 가능함)
*/
print((factorial(N) * mod_inverse((factorial(N - K) * factorial(K)) % div, div - 2)) % div);
}
int factorial(int N) {
if(N == 0) {
return 1;
}
return N * factorial(N - 1);
}
// 역원 구하기
int mod_inverse(int a, int p) {
int ret = 1;
while(p > 0) {
if(p % 2 == 1) {
ret *= a;
p--;
ret %= div;
}
a *= a;
a %= div;
p >>>= 1; // p = p/2 랑 동치
}
return ret;
}
나머지 알고리즘은 모듈러 연산을 바로 적용하면 되는 부분이라 어렵지 않게 풀 수 있다. 다만 이번에 또 하나 고려해야 할 점이 있는데, 입력값이 최대 1000으로 동적계획법을 이용하지 않고 이항계수 풀이를 하면 '시간초과'가 난다.
<시간 초과 알고리즘>
main {
print(BC(N, K));
}
int BC(int N, int K) {
if(N == K || K == 0) {
return 1;
}
return (BC(N - 1, K - 1) + BC(N - 1, K)) % 10007;
}
그러므로 위의 알고리즘에서 동적계획법을 활용하여 아래와 같이 풀어야 한다.
<알고리즘 2>
int[][] dp = new int[N + 1][K + 1];
main {
print(BC(N, K));
}
int BC(int N, int K) {
// 이미 풀었던 sub문제일 경우 값을 재활용
if(dp[N][K] > 0) {
return dp[N][K];
}
if(N == K || K == 0) {
return dp[N][K] = 1;
}
return dp[N][K] = (BC(N - 1, K - 1) + BC(N - 1, K)) % 10007;
}
이를 토대로 코딩을 하면 쉽게 풀 수 있다.
- 3가지 방법을 사용하여 풀이한다.
이 번 문제에서는 Scanner를 따로 쓰지 않고 위 알고리즘의 2가지 방법에 따른 성능 차이를 보고자 한다.
1. 알고리즘 1
2. 알고리즘 2
- 풀이
- 방법 1 : [알고리즘 1]
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static final int div = 10007;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
/*
* n! / ((n-k)! * k!) -> n! * ((n-k)! * k!)^(-1) 으로 변환
* ((n-k)! * k!)^(-1) == ((n-k)! * k!)^(p-2) 동치
* p(=div)가 소수여서 가능함)
*/
System.out.println((factorial(N) * mod_inverse((factorial(N - K) * factorial(K)) % div, div - 2)) % div);
}
static int factorial(int N) {
// factorial(0) == 1 이다.
if (N <= 1) {
return 1;
}
return (N * factorial(N - 1)) % div;
}
// 역원 구하기 (= 제곱승 구하기)
static int mod_inverse(int a, int p) {
int ret = 1;
while(p > 0) {
if(p % 2 == 1) {
ret *= a;
p--;
ret %= div;
}
a *= a;
a %= div;
p >>= 1; // p = p/2 랑 동치
}
return ret;
}
}
앞선 말한 모듈러 역원을 적용하여 구한 방법이다.
- 방법 2 : [알고리즘 2]
이항 계수의 성질을 이용한 풀이에 더해 동적계획법을 추가하여 풀이한 방법이다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
static int[][] dp;
public static final int div = 10007;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
dp = new int[N + 1][K + 1];
System.out.println(BC(N, K));
}
static int BC(int n, int k) {
// 이미 풀었던 sub문제일 경우 값을 재활용
if (dp[n][k] > 0) {
return dp[n][k];
}
if (k == 0 || n == k) {
return dp[n][k] = 1;
}
return dp[n][k] = (BC(n - 1, k - 1) + BC(n - 1, k)) % div;
}
}
크게 어려울 것은 없을 것이다.
- 성능

채점 번호 : 23562345 - 방법 2 : 알고리즘 2
채점 번호 : 23562344 - 방법 1 : 알고리즘 1
보면 단일 재귀 자체는 1000에 그치는지라 그런건지 아니면 오버헤드가 커서 그런건진 몰라도 몇 번 테스트 해보니 알고리즘 1이 더 빠른듯 하다.
- 정리
이 번 문제는 약간 수학적 지식을 요구하여 풀이하는 난이도 있는 문제였다. 아마 위 내용을 완벽하게 이해했다면 다른 이항계수 문제도 문제없이 풀 수 있을 것이다. 물론 역원을 구하는 방법에서 시간을 더 줄일 수는 있으나, 이 부분은 나중에 더 심화해서 다루도록 하겠다. (알고리즘 1에서 역원을 구하는 시간 복잡도는 O(log p)다.)
만약 어려운 부분이 있거나 이해가 안되는 부분이 있다면 댓글 남겨주시면 빠르게 답변드리도록 하겠다.
'JAVA - 백준 [BAEK JOON] > 정수론 및 조합론' 카테고리의 다른 글
| [백준] 1676번 : 팩토리얼 0의 개수 - JAVA [자바] (27) | 2020.11.05 |
|---|---|
| [백준] 9375번 : 패션왕 신해빈 - JAVA [자바] (9) | 2020.11.04 |
| [백준] 11050번 : 이항 계수 1 - JAVA [자바] (18) | 2020.10.27 |
| [백준] 3036번 : 링 - JAVA [자바] (0) | 2020.10.23 |
| [백준] 2981번 : 검문 - JAVA [자바] (10) | 2020.10.22 |