[백준] 11050번 : 이항 계수 1 - JAVA [자바]
11050번: 이항 계수 1
첫째 줄에 \(N\)과 \(K\)가 주어진다. (1 ≤ \(N\) ≤ 10, 0 ≤ \(K\) ≤ \(N\))
www.acmicpc.net
-
문제

- 알고리즘 [접근 방법]
이항 계수(Binomial coefficient) 문제 자체는 매우매우 쉽다. 지금은 배우는지는 모르겠지만 고교과정에서 조합을 배웠다면 쉽게 풀었을 것이다.
en.wikipedia.org/wiki/Binomial_coefficient
Binomial coefficient - Wikipedia
The binomial coefficients can be arranged to form Pascal's triangle, in which each entry is the sum of the two immediately above. Visualisation of binomial expansion up to the 4th power In mathematics, the binomial coefficients are the positive integers th
en.wikipedia.org
이항계수는 위 위키피디아 글에서도 잘 정리가 되어있는데, 이항 계수 말 그대로 '두 개의 항(이항)을 전개하여 계수로 나타낸 것'이다.
쉽게 말하면, (a + b)n 을 전개하였을 때 계수를 의미한다는 것.
예로들어 (a + b)2 = a2 + 2ab + b2 이고, 계수는 {1, 2, 1} 이다.
(a + b)3 = a3 + 3a2b + 3ab2 + b3 이고, 계수는 {1, 3, 3, 1} 이다.
이런식으로 전개하다보면 우리가 어디선가 익숙한 아래와 같은 그림이 나온다.

이게 그 유명한 파스칼의 삼각형이다.
이러한 이항 계수는 n승에 대해 전개하면 다음과 같은 '항'이 나타난다. (계수를 쓰지 않고 항만 쓸 경우)
(a + b)n = {anb0, an-1b1, an-2b2, ⋯ , an-rbr, ⋯ , a2bn-2. a1bn-1, a0bn}
위의 항들 앞에 계수를 구하고자 한다면 결과적으로 다음과 같이 표현 할 수 있다.
(a + b)n 에 대해 전개했을 때, an-rbr에 대한 계수
예로 들어 n = 3 이고, r = 2 라면, a1b2의 계수를 말하는 것이고, 이 때의 계수는 3이다.
그러면 문제는 계수를 어떻게 구하느냐라는 문제만 남았다. 한 번 생각해보자. (a + b)n 에서 계수를 찾는다는 말은 a와 b가 조합되어 나온 값이 된다는 것이다. 무슨 말인지 모르겟다면 한 번 같이 살펴보도록 하자.
(a + b)3 을 전개할 때 이 번에는 b에 번호를 붙여서 보도록 하겠다.
(a + b)3 = (a + b)(a + b)(a + b)
→ (a + b1)(a + b2)(a + b3)
→ a3 + (b1 + b2 + b3)a2 + (b1b2 + b2b3 + b3b1)a + b1b2b3
위 식을 해석해보자면 이렇다.
a3 항은 {b1, b2 ,b3} 중에서 한 개도 뽑지 않는다. 즉, 0개를 뽑는다.
a2 항은 {b1, b2, b3} 중에서 한 개씩 뽑아서 모두 더한 값이다.
a1 항은 {b1, b2, b3} 중에서 두 개씩 뽑아 곱한 뒤 모두 더한 값이다.
a0 항은 {b1, b2, b3} 중에서 세 개를 뽑아 곱한 값이다.
즉, b가 n개 있을 때 이들중에 r개를 뽑는다는 것이다. n개 중에 r개? 그러면 조합 공식이네! 라고 볼 수 있겠다.
한마디로 계수는 nCr 이 되는 것이다.
a3 항은 b들 중 한 개도 뽑지 않으니 3C0 이 되는 것이고,
a2 항은 b들 중 한 개씩 뽑는 것이니 3C1 이 되는 것이고,
a1 항은 b들 중 두 개씩 뽑는 것이니 3C2 가 되는 것이고,
a0 항은 b들 중 세 개 뽑는 것이니 3C3 이 된다.
위의 조합 공식 nCr 을 이용하여 좀 더 정리해서 말하면, 이렇게 표현 할 수 있는 것이다.
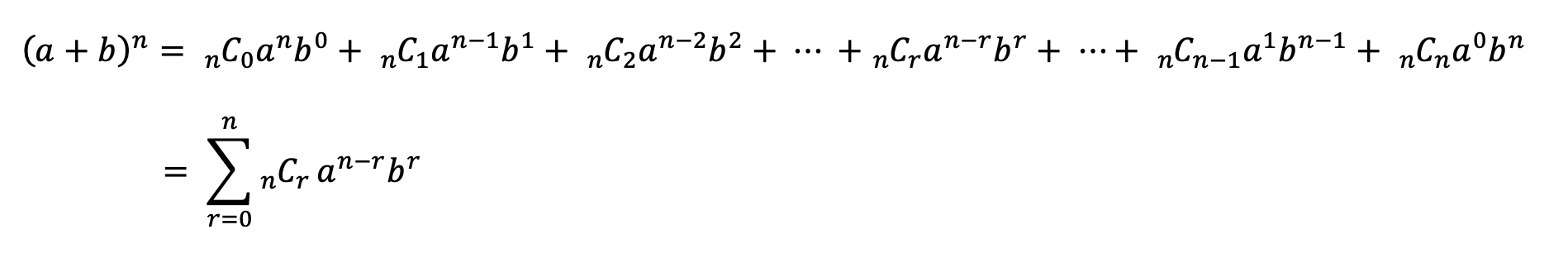
즉, 우리가 구할 계수는 nCr 이 되는 것이다.
그리고 nCr은 다음과 같이 표현하기도 한다.

자, 그러면 팩토리얼로 r(문제에서는 k) 팩토리얼과, n-r 팩토리얼과, n 팩토리얼을 구해서 위 수식에 대입하면 되는 것이다. 알고리즘으로 보자면 다음과 같겠다.
<알고리즘 1>
main {
print(factorial(N) / (factorial(K) * factorial(N - K)));
}
int factorial(int N) {
if(N == 0) {
return 1;
}
return N * factorial(N - 1);
}
위와 같이 풀어도 문제를 통과할 수는 있다. 근데 각 수마다 팩토리얼을 구해주자니 뭔가 불편하다.
그래서 팩토리얼로 하나하나 구해주지 말고, 하나로 합쳐보고자 한다.
아래의 조합의 성질을 조금만 이해한다면 쉽게 가능하다. 알고리즘을 보여주기 전에 두 가지 성질에 대해 잠깐 알아보자.
[1번 성질]
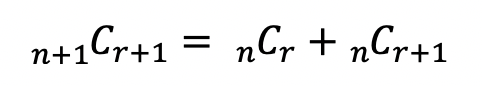
이 공식은 워낙 유명한 공식이라 다 알 것이다. 만약 모른다 하더라도, 맨 처음 파스칼의 삼각형을 보면 바로 이해할 수 있다. 그리고 위 식을 좀 더 간단하게 쓴다면 아래와 같이 쓸 수 있다.
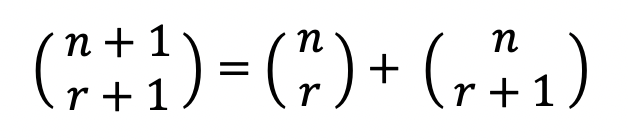
만약 n과 r의 이항계수를 구한다면 이렇게 나타내질 것이다.

위 점화식을 흔히 '파스칼의 법칙'이라 한다.
[2번 성질]
그리고 추가로 n과 r이 같거나, r=0 이라면 1이라는 것은 자명하다. 즉, 다음과 같은 식을 만족한다.

좀 더 간단하게 표현하면 다음과 같다.

위 두 성질을 이용하여 알고리즘을 짜보자면 다음과 같이 하나의 식으로 완성할 수 있다.
<알고리즘 2>
main {
print(BC(N, K));
}
int BC(int N, int K) {
// 2번 성질
if(N == K || K == 0) {
return 1;
}
// 1번 성질
return BC(N - 1, K - 1) + BC(N - 1, K);
}
위와 같이 각각의 팩토리얼을 구하는 방식이 아닌 하나의 식으로 재귀를 통해 완성할 수 있다.
하지만, 아주 큰 문제가 하나 있다. 우리가 그동안 배우면서 재귀를 사용하여 '부분 문제'를 풀 경우 중복되는 부분 문제더라도 또 다시 풀어야 한다는 점이다.
(만약 잘 모를 경우 아래 링크 참고)
[백준] 2748번 : 피보나치 수 2 - JAVA [자바]
st-lab.tistory.com
결국 재귀로 서브 문제에 대해 풀 경우 memoization(메모이제이션)을 하지 않으면 함수의 성능이 매우 떨어지기 때문에, 우리가 이미 풀었던 경우는 메모이제이션을 해주어야 좀 더 효율이 좋은 함수를 만들 수 있다.
즉, 동적계획법을 이용하는 것이다.
쉽게 말해서 알고리즘 2 코드에 메모이제이션을 할 배열을 초기에 선언하고, 재귀로 하위 문제로 접근하고, 문제가 풀리면 메모이제이션을 할 배열에 저장하면서 나오는 것이다. 코드로 보면 바로 이해 갈 것이다.
<알고리즘 3>
int[][] dp = new int[N + 1][K + 1];
main {
print(BC(N, K));
}
int BC(int N, int K) {
// 이미 풀었던 sub문제일 경우 값을 재활용
if(dp[N][K] > 0) {
return dp[N][K];
}
// 2번 성질
if(N == K || K == 0) {
return dp[N][K] = 1;
}
// 1번 성질
return dp[N][K] = BC(N - 1, K - 1) + BC(N - 1, K);
}
이렇게 총 3가지의 풀이 방법을 알려주었다.
- 3가지 방법을 사용하여 풀이한다.
이번 포스팅에서는 입력방법을 BufferedReader로만 사용하고자 한다. 대신 알고리즘에 따른 차이를 볼 것이고, 만약 Scanner로 입력받고싶을 경우 입력 부분만 수정하면 된다.
1 . 알고리즘 1
2. 알고리즘 2
3. 알고리즘 3
- 풀이
- 방법 1 : [알고리즘 1]
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
// nCk = n! / ((n-k)! * k!)
System.out.println(factorial(N) / (factorial(N - K) * factorial(K)));
}
static int factorial(int N) {
// factorial(0) == 1 이다.
if (N <= 1) {
return 1;
}
return N * factorial(N - 1);
}
}
가장 기본적인 방법이라 할 수 있겠다.
맨 처음 알려주었던 방법 그대로다. 그리고 중요한 점은 0! (0팩토리얼) = 1 이다. 0이 아니라는 걸 명심하자.
- 방법 2 : [알고리즘 2]
각각 팩토리얼을 구하는 방법이 아닌 이항 계수의 성질을 이용하여 하나의 식으로 만들어보았었다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
System.out.println(BC(N, K));
}
static int BC(int n, int k) {
// 2번 성질
if(n == k || k == 0) {
return 1;
}
// 1번 성질
return BC(n - 1, k - 1) + BC(n - 1, k);
}
}
참고로 BC는 Binomial coefficient(이항 계수)의 약자다.
- 방법 3 : [알고리즘 3]
위 방법 2에 동적계획법을 더한 방법이다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
static int[][] dp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
dp = new int[N + 1][K + 1];
System.out.println(BC(N, K));
}
static int BC(int n, int k) {
// 이미 풀었던 sub문제일 경우 값을 재활용
if (dp[n][k] > 0) {
return dp[n][k];
}
// 2번 성질
if (k == 0 || n == k) {
return dp[n][k] = 1;
}
// 1번 성질
return dp[n][k] = BC(n - 1, k - 1) + BC(n - 1, k);
}
}
위와같이 동적계획법을 이용하면 이론상으로는 시간복잡도가 선형시간 O(N) 이다.
물론 Top-Down 방식이 아닌 Bottom-Up방식으로도 구현할 수는 있으니 아래 더보기에서 참고하실 수 있도록 올려두겠다.
[Bottom-Up 방식]
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int[][] dp = new int[N + 1][K + 1];
// 2번 성질 (n == k)
for (int i = 0; i <= K; i++) {
dp[i][i] = 1;
}
// 2번 성질 (k == 0)
for(int i = 0; i <= N; i++) {
dp[i][0] = 1;
}
for (int i = 2; i <= N; i++) {
for (int j = 1; j <= K; j++) {
// 1번 성질
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
}
}
System.out.println(dp[N][K]);
}
}
- 성능

채점 번호 : 23501528 - 방법 3 : 알고리즘 3
채점 번호 : 23501521 - 방법 2 : 알고리즘 2
채점 번호 : 23501513 - 방법 1 : 알고리즘 1
이번 문제의 경우 입력의 범위가 워낙 작아서 알고리즘상의 큰 차이는 없는 것 같다..
- 정리
아마 이항 계수에 대해 알고있다면 대부분은 nCr 공식을 바로 떠올리고 이용하여 쉽게 풀었을 것이다. 그러나 혹시 잘 몰랐다거나 왜 조합 공식이 유도되는지 궁금하신 분들이 있을까 해서 어떻게 그런 공식이 나오는지를 한 번 정리해서 풀이를 해보았다.
고등학교 때는 수학을 좋아했음에도 유독 확률 파트가 약했던 필자... 그 때는 그냥 이 것은 이렇다! 라는 식으로 외웠던지라 공식도 까먹고 점수도 까먹었지만 나중에와서 돌이켜보면 확실히 이렇게 한 번 정리를 하면 기억에도 오래남고, 설령 까먹더라도 유도하여 공식을 도출할 수도 있는 것 같다.
만약 어려운 부분이나 이해가 안되는 부분이 있다면 댓글 남겨주시면 언제든 답변해드리니 부담말고 댓글 남기시면 좋겠다.
'JAVA - 백준 [BAEK JOON] > 정수론 및 조합론' 카테고리의 다른 글
| [백준] 9375번 : 패션왕 신해빈 - JAVA [자바] (9) | 2020.11.04 |
|---|---|
| [백준] 11051번 : 이항 계수 2 - JAVA [자바] (12) | 2020.10.30 |
| [백준] 3036번 : 링 - JAVA [자바] (0) | 2020.10.23 |
| [백준] 2981번 : 검문 - JAVA [자바] (10) | 2020.10.22 |
| [백준] 2609번 : 최대공약수와 최소공배수 - JAVA [자바] (14) | 2020.10.20 |