자바 [JAVA] - Linked Hash Set (연결 해시 셋) 구현하기
자료구조 관련 목록 링크 펼치기
0. 자바 컬렉션 프레임워크 (Java Collections Framework)
3. 단일 연결리스트 (Singly LinkedList)
4. 이중 연결리스트 (Doubly LinkedList)
6. 스택 (Stack)
11. 연결리스트 덱 (LinkedList Deque)
12. 배열 힙 (Heap)
15. 해시 셋 (Hash Set)
16. 연결 해시 셋 (Linked Hash Set) - [현재 페이지]
17. 이진 탐색 트리 (Binary Search Tree)
- Linked Hash Set
오늘은 연결된 해시 셋을 구현해보고자 한다.
이름에서도 나오듯이 Link + Hash + Set의 복합 자료구조다. 쉽게 말해서 이전에 구현했던 LinkedList와 HashSet의 특성을 같이 갖는 형태라고 보면 된다.
그렇기 때문에 글을 읽기 전에 기본적으로 두 가지 구현 방식은 반드시 알고가야 구현하는데 어려움이 없을 것이다.
Hash Set <- 특히 HashSet을 기반으로 구현 할 것이기 때문에 읽고오지 않으면 이해하기 어려울 것이다.
또한 Set Interface 글도 반드시 읽고 오시길 바란다. 왜냐하면, 아래 링크에서도 언급이 되지만, 원래 Set 자료구조는 내부적으로 모두 Map으로 구현이 된다. 하지만, Map을 먼저 구현하고 Set을 다루기도 애매모호 해지고, 그렇다고 Map하고 같이 다루자니 글이 너무 길어지거니와 필요 없는 부분이 많아지기 때문이다. 그러니 한 번 읽고 오신 다음에 이 글을 보시는 것이 좀 더 이해가 빠를 것이다.
오늘은 Set의 일종인 연결 해시 셋(Linked Hash Set) 에 대해 알아보고자 한다.
만약 필자의 Set 인터페이스 구현을 보고 오셨거나 이전의 HashSet을 보았다면 알겠지만, Set은 '중복 원소를 허용하지 않는다'가 포인트라고 했다.
그러면 Linked HashSet은 이전 HashSet과는 무슨 차이일까? 바로 '입력 순서를 지킨다'는 것이다.
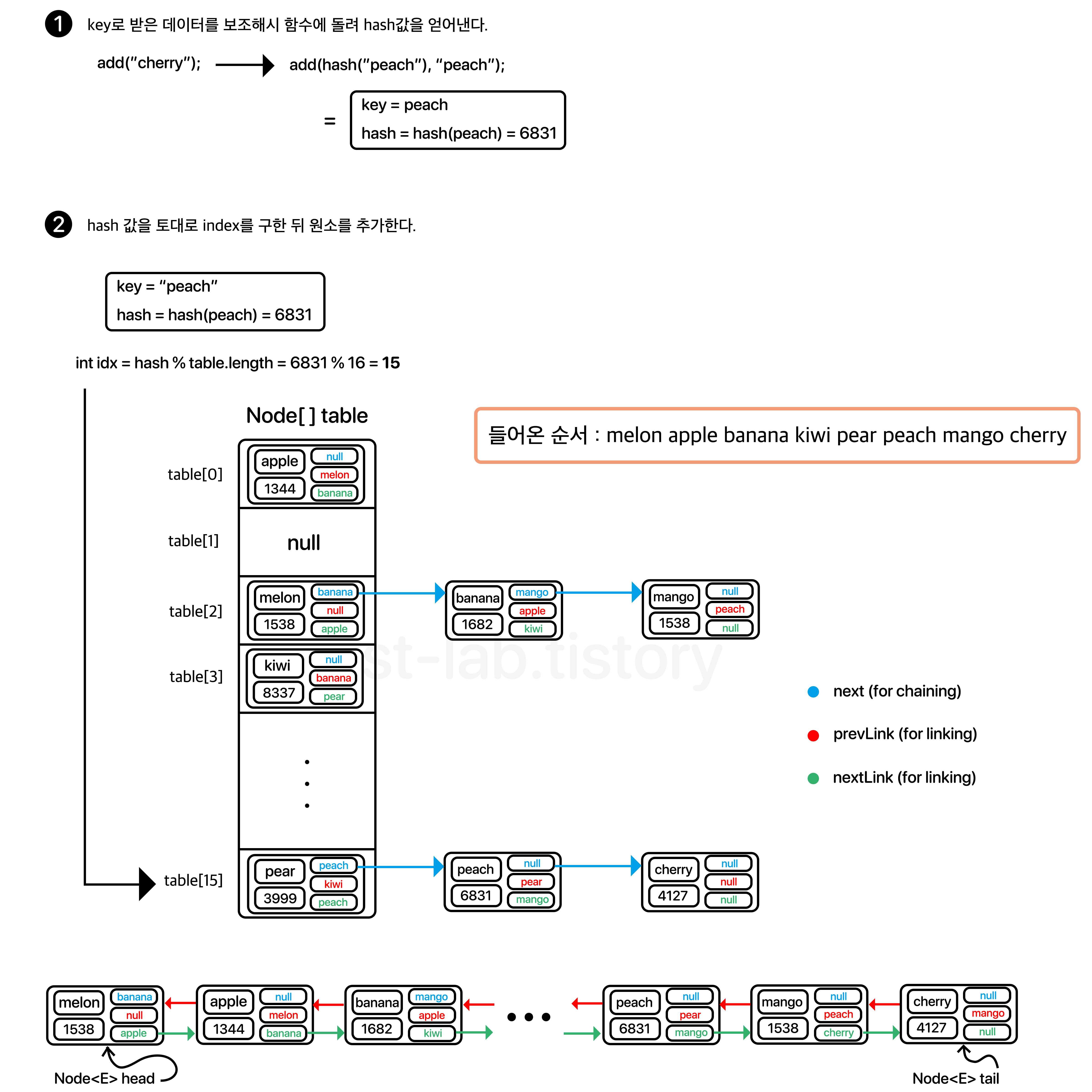
생각해보자. HashSet을 구현했을 때, 기본적으로 우리는 데이터를 해싱한 값을 Node[] table 배열의 인덱스(index)로 활용하여 해당 인덱스에 데이터를 저장했다. 이는 데이터에 대해 빠르게 탐색할 수 있는 장점이 있지만, 데이터가 해싱된 값에 따라 저장되는 위치가 달라지기 떄문에 결정적으로 순서가 보장되지 않는다.
이러한 단점을 보완하기 위해 우리가 LinkedList를 구현할 때, 노드 클래스에는 이전 노드를 가리키는 변수인 prev와 다음 노드를 가리키는 next 변수를 두고, LinkedList 클래스에서는 연결 된 노드들의 첫 번째 노드를 가리키는 head와 마지막 노드를 가리키는 tail 변수를 두어 노드들을 상호 연결을 해주듯 같은 원리로 HashSet 구현과 동일하게 table에 저장하되, 순서를 보장할 수 있도록 LinkedList 의 구현 기능을 추가해준 것이다.
매우 간단하게 말하자면, 이전의 HashSet 구현과 같되, LinkedList처럼 연결해주는데 필요한 변수만 추가 된 것이다.
아마 위 말만으로는 이해하기 힘들 것이다. 한 번 이미지를 보면서 이해해보도록 하자.
(참고로 table에 데이터를 저장하는 방식은 Separate Chaining 방식으로 이전의 HashSet 구현과 동일하므로 여기서 따로 설명은 안하겠다.)

(아래는 linkedlist형식으로 연결 된 것을 보여준 것이다. 실제로는 위 두 개가 하나라고 보시면 된다. 쉽게 말해 table에 담기면서 아래처럼 서로 linkedlist처럼 참조를 통해 연결되어있다.)
- Node 구현
그러면 우리가 Node를 기반으로 하는 배열(table)을 이용한 LinkedHashSet를 구현하기에 앞서 가장 기본적인 데이터를 담을 Node 클래스를 먼저 구현하고자 한다. 이 때 Node 클래스는 앞으로 구현 할 LinkedHashSet와 같은 패키지에 생성할 것이다. 만약 다른 패키지에 생성하면 LinkedHashSet 구현 할 때 'import Node클래스가 있는 패키지 경로.Node;' 를 해주면 된다. (또는 LinkedHashSet 클래스 내에 static class로 생성해주어도 무방하다.)
[Node.java]
class Node<E> { final int hash; final E key; Node<E> next; // for Separate Chaining Node<E> nextLink; // for linked list(set) Node<E> prevLink; // for linked list(set) public Node(int hash, E key, Node<E> next) { this.hash = hash; this.key = key; this.next = next; this.nextLink = null; this.prevLink = null; } }
- LinkedHashSet 구현
- 사전 준비
[Set Interface 소스]
[Set.java]
package Interface_form; /** * * 자바 Set Interface입니다. <br> * Set은 HashSet, LinkedHashSet, * TreeSet에 의해 구현됩니다. * * @author st_lab * @param <E> the type of elements in this Set * * @version 1.0 * */ public interface Set<E> { /** * 지정된 요소가 Set에 없는 경우 요소를 추가합니다. * * @param e 집합에 추가할 요소 * @return {@code true} 만약 Set에 지정 요소가 포함되지 않아 정상적으로 추가되었을 경우, * else, {@code false} */ boolean add(E e); /** * 지정된 요소가 Set에 있는 경우 해당 요소를 삭제합니다. * * @param o 집합에서 삭제할 특정 요소 * @return {@code true} 만약 Set에 지정 요소가 포함되어 정상적으로 삭제되었을 경우, * else, {@code false} */ boolean remove(Object o); /** * 현재 집합에 특정 요소가 포함되어있는지 여부를 반환합니다. * * @param o 집합에서 찾을 특정 요소 * @return {@code true} Set에 지정 요소가 포함되어 있을 경우, * else, {@code false} */ boolean contains(Object o); /** * 지정된 객체가 현재 집합과 같은지 여부를 반환합니다. * * @param o 집합과 비교할 객체 * @return {@code true} 비교할 집합과 동일한 경우, * else, {@code false} */ boolean equals(Object o); /** * 현재 집합이 빈 상태(요소가 없는 상태)인지 여부를 반환합니다. * * @return {@code true} 집합이 비어있는 경우, * else, {@code false} */ boolean isEmpty(); /** * 현재 집합의 요소의 개수를 반환합니다. * * @return 집합에 들어있는 요소의 개수를 반환 */ int size(); /** * 집합의 모든 요소를 제거합니다. * 이 작업을 수행하면 비어있는 집합이 됩니다. */ void clear(); }
[구현 바로가기]
<필수 목록>
◦ size, isEmpty, contains, clear, equals 메소드 구현
◦ 전체 코드
[LinkedHashSet 클래스 및 생성자 구성하기]
이번에 구현 할 LinkedHashSet은 이전의 HashSet 구현과 메커니즘이 같다. Node 배열에 데이터를 저장하되, 각 노드의 link 변수로 순서에 맞게 노드들을 참조하는 방식으로 구현된다는 것을 알았으면 한다. LinkedHashSet 이라는 이름으로 생성한다.
또한 Set Interface 포스팅에서 작성했던 Set 인터페이스를 implements 해준다. (필자의 경우 인터페이스는 Interface_form 이라는 패키지에 생성해두었다.)
implements 를 하면 class 옆에 경고표시가 뜰 텐데 인터페이스에 있는 메소드들을 구현하라는 것이다. 어차피 모두 구현해나갈 것이기 때문에 일단은 무시한다.
[LinkedHashSet.java]
import Interface_form.Set; public class LinkedHashSet<E> implements Set<E> { // 최소 기본 용적이며 2^n꼴 형태가 좋다. private final static int DEFAULT_CAPACITY = 1 << 4; // 3/4 이상 채워질 경우 resize하기 위한 임계값 private static final float LOAD_FACTOR = 0.75f; Node<E>[] table; // 요소의 정보를 담고있는 Node를 저장할 Node타입 배열 private int size; // 요소의 개수 // 들어온 순서를 유지할 linkedlist private Node<E> head; // 노드의 첫 부분 private Node<E> tail; // 노드의 마지막 부분 @SuppressWarnings("unchecked") public LinkedHashSet() { table = (Node<E>[]) new Node[DEFAULT_CAPACITY]; size = 0; head = null; tail = null; } // 보조 해시 함수 (상속 방지를 위해 private static final 선언) private static final int hash(Object key) { int hash; if (key == null) { return 0; } else { // hashCode()의 경우 음수가 나올 수 있으므로 절댓값을 통해 양수로 변환해준다. return Math.abs(hash = key.hashCode()) ^ (hash >>> 16); } } }
변수와 함수부터 먼저 차례대로 설명해주도록 하겠다.
DEFAULT_CAPACITY : Node 배열의 기본 및 최소 용적이다. 한마디로 요소를 담을 배열의 크기를 의미한다. 배열을 동적으로 관리 할 때 최소 크기가 1<<4, 즉 16 미만으로 내려가지 않기 위한 변수다. 그리고 요소의 개수랑은 다른 의미이므로 이 점 헷갈리지 말자.
LOAD_FACTOR : 앞서 말했듯 테이블의 크기에 비해 데이터양이 일정 이상 많아지면 성능이 저하된다고 했다. 그 기준점을 0.75로 잡아 75%가 넘으면 배열의 용적을 늘릴 수 있도록 기준이 되는 변수다.
size : 배열에 전체 요소(원소)의 Node 개수 변수
table : 요소(Node)를 담을 배열이다.
head : 리스트의 가장 첫 노드를 가리키는 변수다.
tail : 리스트의 가장 마지막 노드를 가리키는 변수다.
여기서 보조해시 함수인 hash() 메소드가 있다.
물론 반드시 필요한 것은 아니다. 요즘에는 hash 함수도 고른 분포를 갖을 수 있게 설계되어있기 때문에 큰 역할을 하지는 못하지만, 원래는 최대한 해시충돌을 피하기 위해 보조해시함수를 써서 고른 분포를 할 수 있도록 하기 위한 함수가 바로 위와같은 보조 해시 함수다.
여기서는 Java11 의 구현유사하게 key의 hashCode() 의 절댓값과 그 값을 16비트 왼쪽으로 밀어낸 값하고의 XOR 값을 반환하도록 만들었다.
(이후 구현할 것이지만, 만약 나머지 연산(%)을 할 경우에는 hashCode() 값이 음수가 나올 때를 고려하여 Math.abs() 함수를 써야하나, 만약 비트 &(AND) 연산을 통해 할 경우 Math.abs()를 써줄 필요가 없다는 점 미리 알린다.)
그리고 이 번 HashSet에서는 사용자 용적 설정을 할 수 있는 생성자를 따로 두지 않았다.
이 후에 보면 알겠지만, HashSet의 용적을 2^n 꼴로 두는 것이 매우 편리하고 좋기 때문이다. 또한 사용자가 해시충돌을 예측하기 어렵고, 해시충돌이 발생하더라도 Separate Chaining 방식으로 연결되기 때문에 굳이 사용자에게 용적을 설정하게 둘 필요는 없다.
즉, 여기서 설명하는 모든 건 기본적으로 table의 용적이 2^n 꼴임을 알아두시길 바란다.
[add 메소드 구현]
오늘도 마찬가지로 기존과는 다른 조금 특별하게 resize() 가 아닌 add() 메소드 부터 설명하도록 하겠다.
일단 원소 추가 과정을 통해 HashSet의 기본 골자를 이해하는 것이 좋을 것이다. 왜냐하면 add과정 자체는 HashSet의 add와 과정이 동일하고, 마지막에 노드에 대해 '링크'하는 것이 추가되는 것 뿐이기 때문이다.
그러면 일단, DoublyLinkedList처럼 노드를 link하는 메소드부터 살펴보자. 순서만 유지하면 되기 때문에 굳이 중간 삽입 같은 것을 고려 할 필요가 없다. 쉽게 말해 '마지막 노드에 새 노드를 연결'해주기만 하면 된다.
private void linkLastNode(Node<E> o) { Node<E> last = tail; // 마지막 노드를 갖고온다. tail = o; // tail을 새로운 노드 o가 가리키도록 갱신해준다. /* * 만약 마지막 노드가 null이라는 것은 노드에 저장된 데이터가 없는, * 즉 head 노드도 null인 상태라는 것이다. * 그러므로 head도 새 노드인 o를 가리키도록 한다. */ if (last == null) { head = o; } /* * last가 null이 아닐경우 새 노드 o의 앞의 노드를 가리키는 노드를 last로 두고, * last의 다음 노드는 새 노드인 o를 가리키도록 한다. */ else { o.prevLink = last; last.nextLink = o; } }
위 메소드 작성이 완료가 되었다면, 이전에 갖고왔던 HashSet의 add부분 코드를 이해를 해야한다. 이 부분은 이전 포스팅하고 내용 자체가 갖기 때문에 더보기로 남겨놓겠다.
HashSet의 경우 기본적으로 HashSet은 '중복 된 값을 허용하지 않는다'를 생각해야 했었다.
즉, 사용자가 추가한 data는 key를 의미하고, 이 key에 대한 hash 값을 얻어 table 배열의 위치를 지정하여 해당 위치에 노드를 추가해야한다.
말로하면 어려울테니.. 한 번 이미지로 보도록 하자.
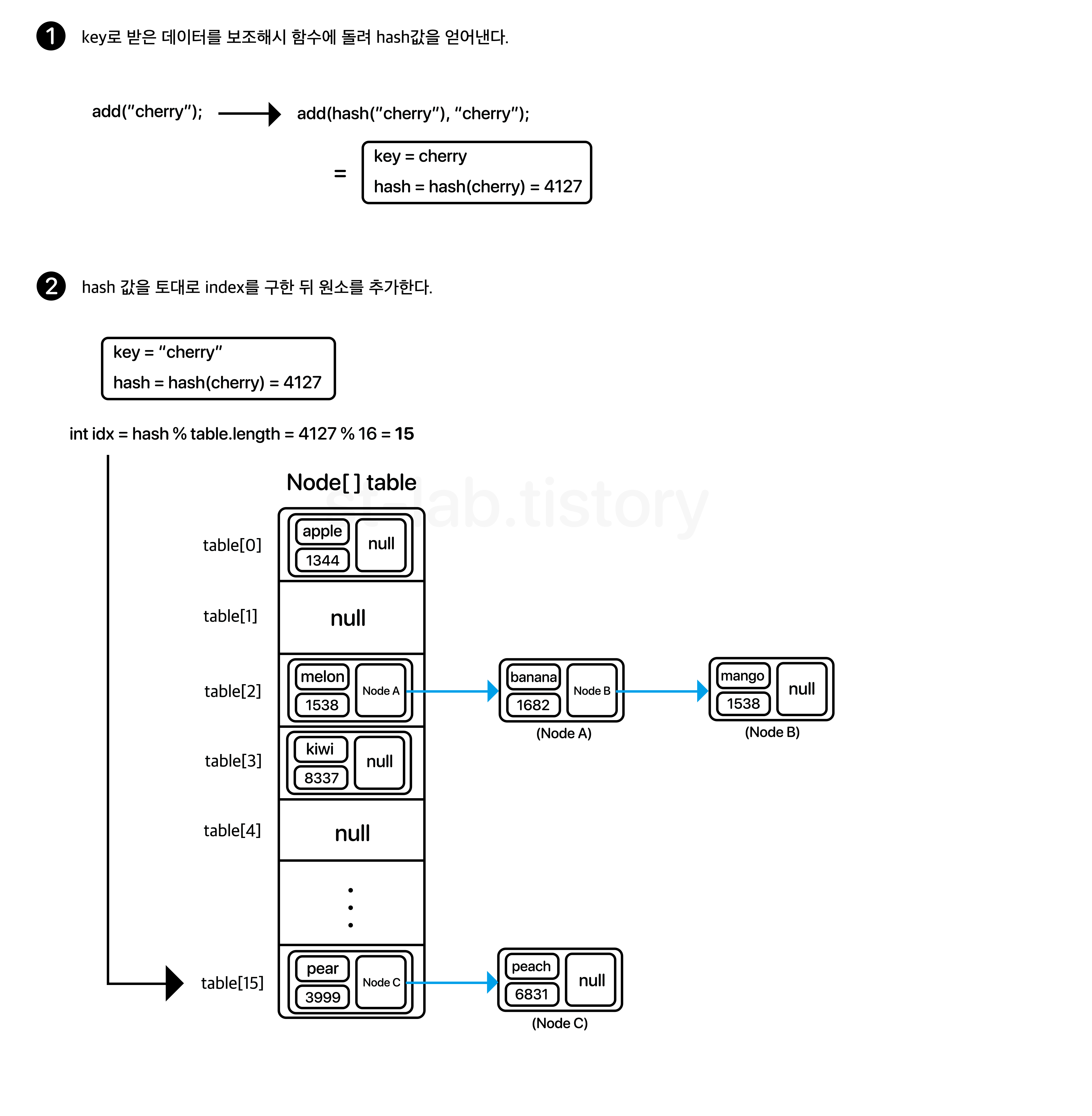
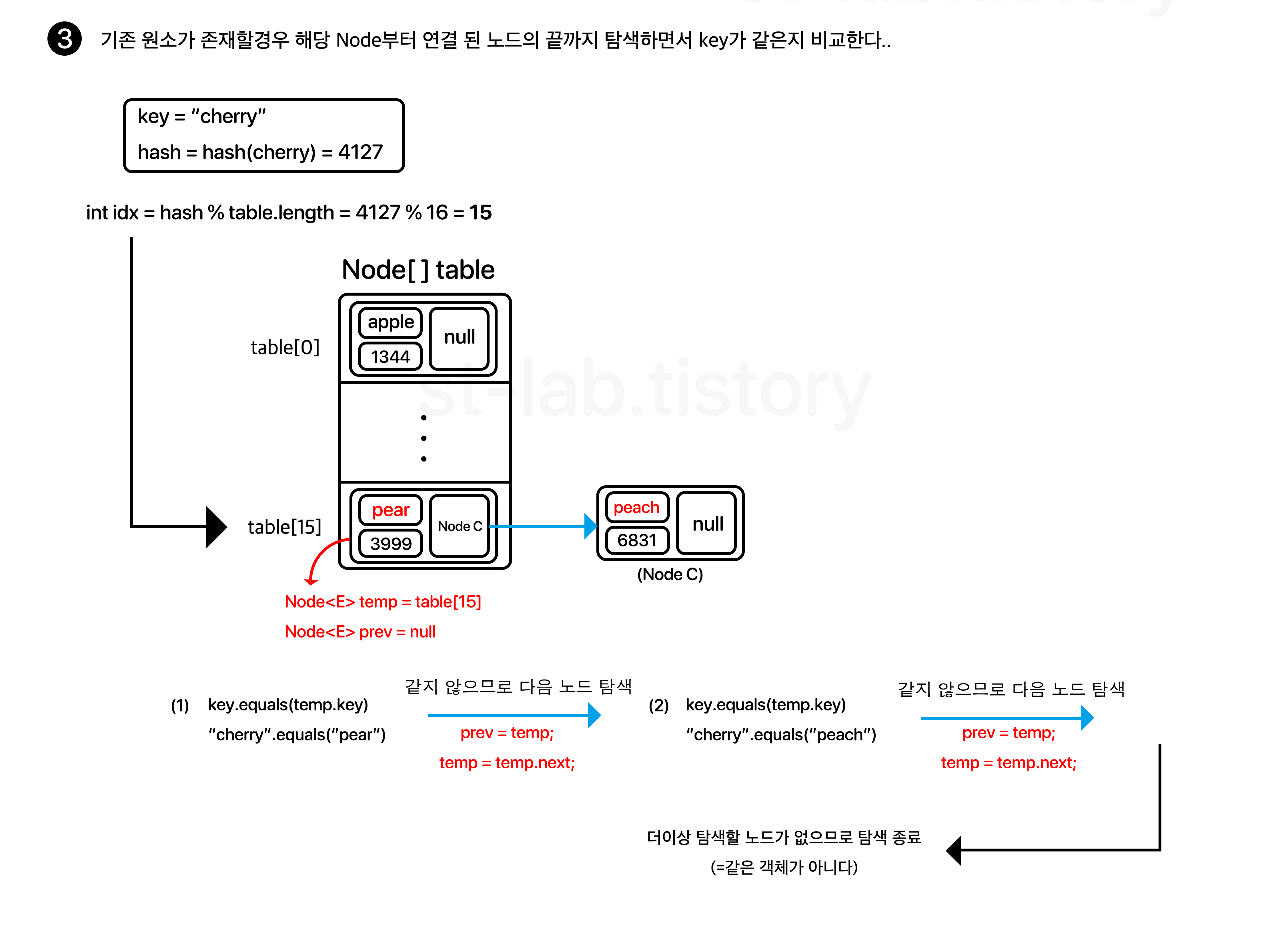
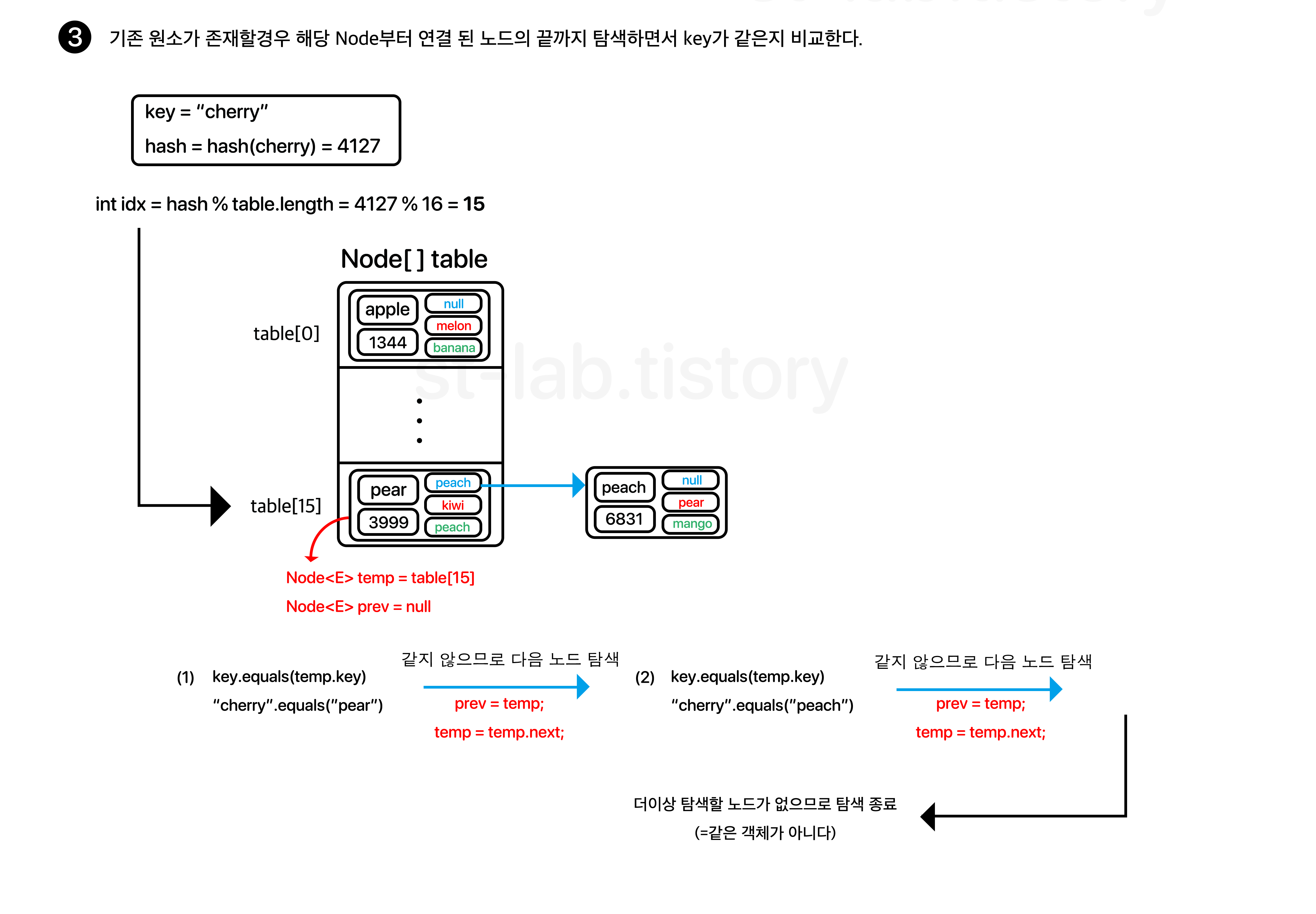
(참고로 각 데이터의 hash값은 이해하기 쉬우라고 임의의 값을 설정한 것일 뿐 실제로 저 값을 갖진 않는다. 오해 없으시길 바란다.)
그리고 중요한 점은 위 이미지에서는 비교를 equals()수준에서만 했지만, 좀 더 정확하게 하려면 다음과 같이 객체를 비교하는 것이 올바르다.
1. hash값이 같은지
2. 주소값이 같거나 혹은 key객체가 같은 내용인지
위 1번 조건과 2번 조건을 둘다 만족해야 추가할 수 있도록 하는 것이 좀 더 정확하게 만들 수 있다.
이미지로 보아도 좀.. 어려울 수는 있으나.. 최대한 쉽게 설명할 수 있도록 노력해보았으니 혹여 이해가 안된다면 댓글 남겨주시면 된다.
코드도 최대한 이해하기 쉽게 주석을 달아놓겠다.
public boolean add(E e) { // key(e)에 대해 만들어두었던 보조해시함수의 값과 key(데이터 e)를 보낸다. return add(hash(e), e) == null; } private E add(int hash, E key) { int idx = hash % table.length; // table[idx] 가 비어있을 경우 새 노드 생성 if (table[idx] == null) { table[idx] = new Node<E>(hash, key, null); } /* * talbe[idx]에 요소가 이미 존재할 경우(==해시충돌) * * 두 가지 경우의 수가 존재 * 1. 객체가 같은 경우 * 2. 객체는 같지 않으나 얻어진 index가 같은 경우 */ else { Node<E> temp = table[idx]; // 현재 위치 노드 Node<E> prev = null; // temp의 이전 노드 // 첫 노드(table[idx])부터 탐색한다. while (temp != null) { /* * 만약 현재 노드의 객체가 같은경우(hash값이 같으면서 key가 같을 경우)는 * HashSet은 중복을 허용하지 않으므로 key를 반납(반환) * (key가 같은 경우는 주소가 같거나 객체가 같은 경우가 존재) */ if ((temp.hash == hash) && (temp.key == key || temp.key.equals(key))) { return key; } prev = temp; temp = temp.next; // 다음노드로 이동 } // 마지막 노드에 새 노드를 연결해준다. prev.next = new Node<E>(hash, key, null); } size++; // 데이터의 개수가 현재 table 용적의 75%을 넘어가는 경우 용적을 늘려준다. if (size >= LOAD_FACTOR * table.length) { resize(); // 아직 미구현 상태임 } return null; // 정상적으로 추가되었을 경우 null반환 }
만약 데이터 요소들이 현재 테이블의 75%정도 이상 차면 배열의 크기를 늘려야 성능을 유지시킬 수 있기 때문에 용적을 재조정 해주어야 한다. 즉, 맨 처음 클래스 선언 및 생성자를 구현해줬을 때 사용했던 LOAD FACTOR 값을 이용하여 일정 이상 차면 resize()를 호출해줄 것이다.
지금 구현은 안되어 있지만, 바로 다음에 resize()를 구현할 것이니 걱정 안하셔도 된다.
위 내용을 이해했다면 HashSet 과정에서 원소가 추가가 된다면 앞서 구현한 LinkedLastNode 메소드만 호출해주면 된다는 것을 이해할 수 있을 것이다.
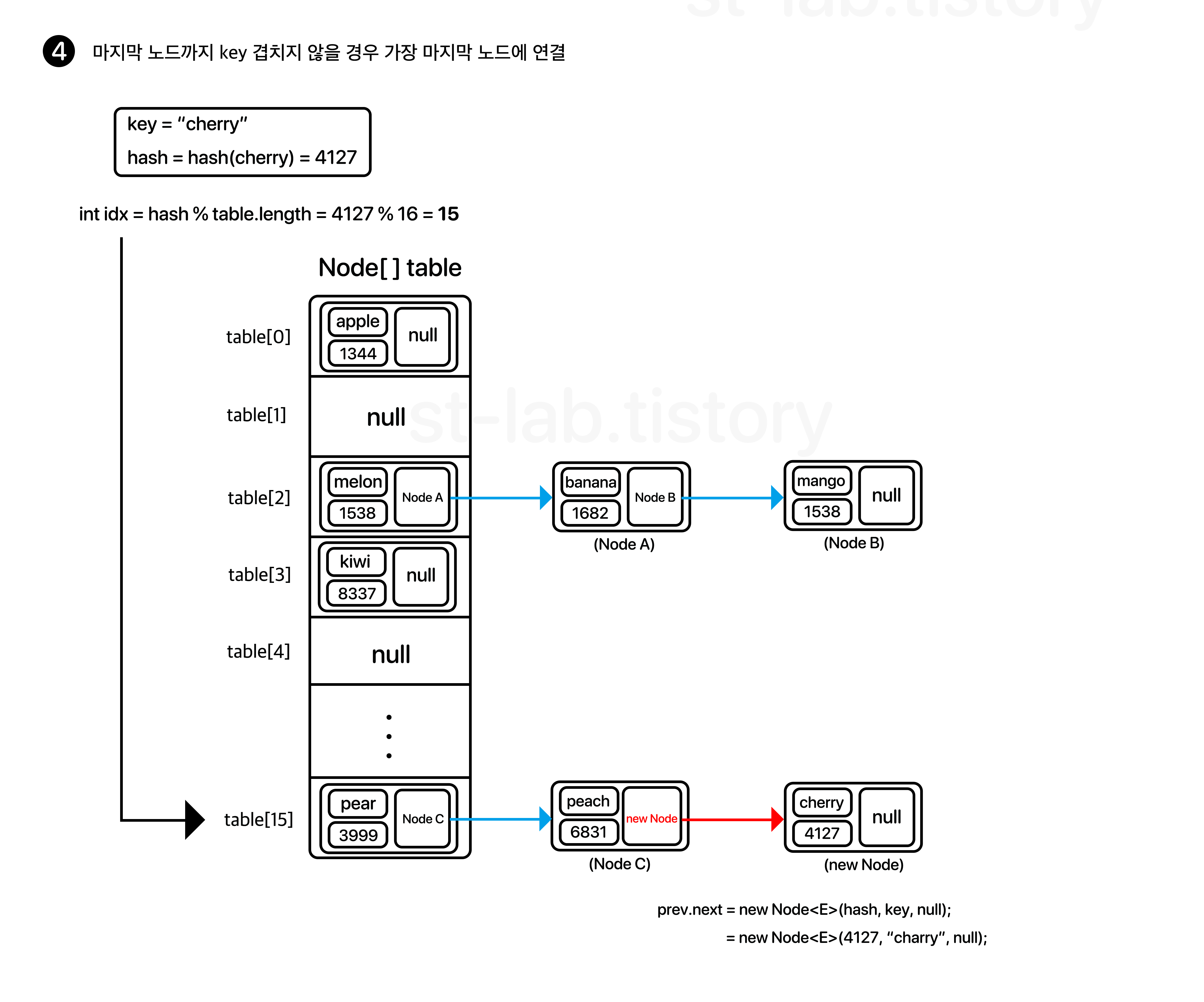
그러면 한 번 LinkedHashSet의 추가 과정을 보도록 하자.

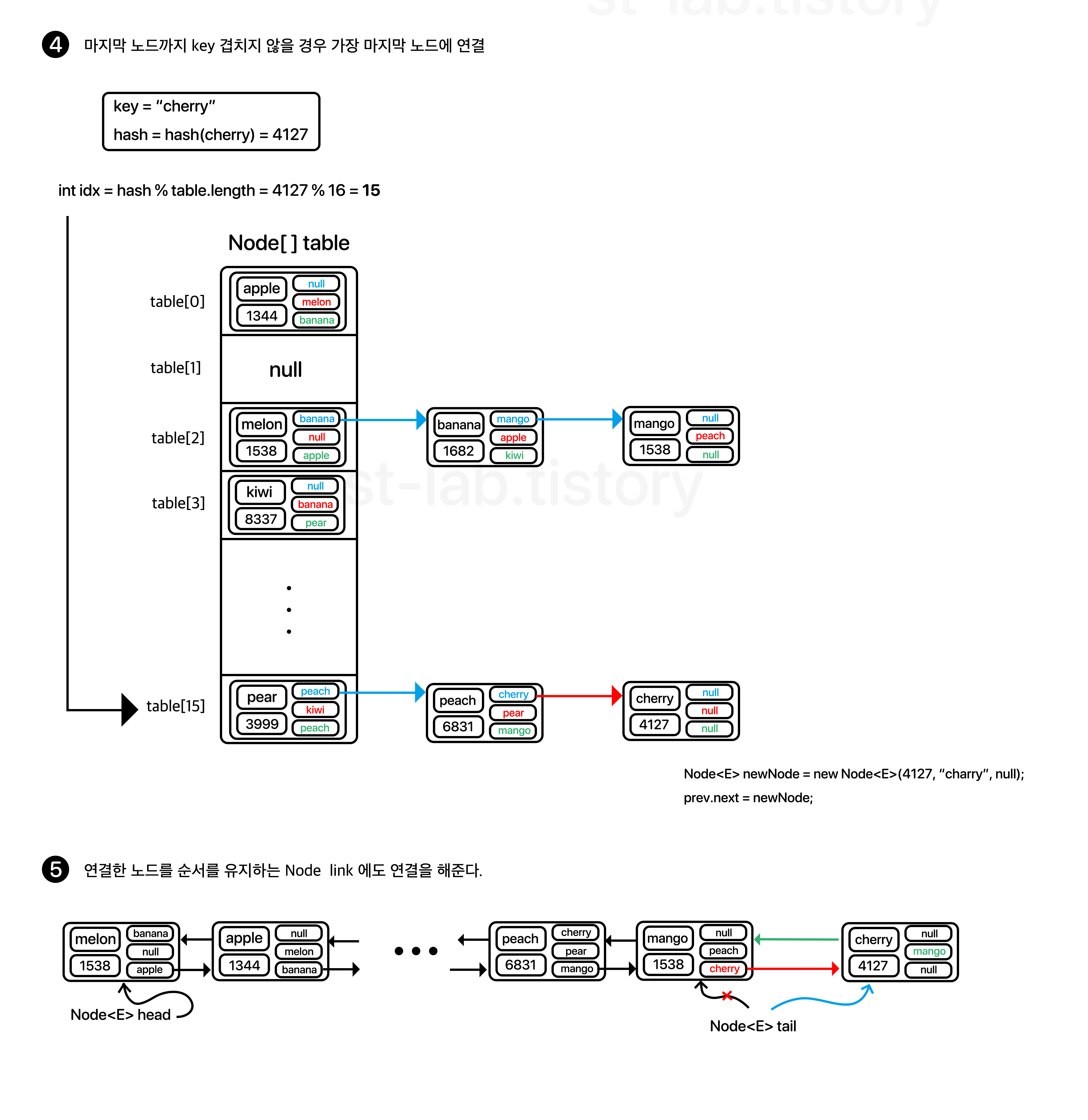
보면 전체적인 과정은 기존의 HashSet과 다를게 없다는 걸 볼 수 있다. 마지막에 Node들의 순서를 유지시키기 위한 link만 추가해주면 끝인 것이다.
이를 코드로 보면 다음과 같다.
@Override public boolean add(E e) { return add(hash(e), e) == null; } private E add(int hash, E key) { int idx = hash % table.length; Node<E> newNode = new Node<E>(hash, key, null); // 새로운 노드 if (table[idx] == null) { table[idx] = newNode; } else { Node<E> temp = table[idx]; Node<E> prev = null; // 해당 인덱스의 마지막 체인 노드까지 탐색 while (temp != null) { // 동일 객체라면 저장하지 않고 key를 반납 if ((temp.hash == hash) && (temp.key == key || temp.key.equals(key))) { return key; } prev = temp; temp = temp.next; } prev.next = newNode; } size++; linkLastNode(newNode); // table에 저장이 끝났으면 해당 노드를 연결해준다. // 데이터의 개수가 현재 table 용적의 75%을 넘어가는 경우 용적을 늘려준다. if (size >= LOAD_FACTOR * table.length) { resize(); // 다음 챕터에서 구현 예정 } return null; }
지금 구현은 안되어 있지만, 바로 다음에 resize()를 구현할 것이니 걱정 안하셔도 된다.
[참고]
여기서 배치 할 인덱스를 구할 때, hash % table.length로 구하는 방법이 가장 일반적이지만, 만약 비트논리연산에 대한 이해가 조금 있다면 2^n꼴로 구현될 경우에는 비트연산을 이용해도 같은 값을 갖는다는 것을 알 수 있다.
int idx = hash % table.length; int idx = hash & (table.legnth - 1); /* 2의 n승 꼴은 비트로 표현하면 다음과 같다. 0000..001000...00(2) <-- n번째 자리에 1이 됨을 의미 위 식에서 1을 빼면 n-1번째 및 하위의 비트는 모두 1이 됨 0000..000111...11(2) hash & 0000..000111...11(2) 이는 즉, 2^n승으로 떨어지는 값 및 그 상위 비트 부분은 제외된, hash와 AND연산이 되므로 이는 곧 hash에 2^n을 나눈 나머지 값이 됨. */
단, 용적(table.length)이 2^n 꼴일 때 가능한 것이므로 만약 용적을 사용자의 입력에 따라 설정해주고자 하는경우에는 위와 같이 할 수 없고 hash % table.length로 해야한다는 점 유의하길 바란다.
그래서 필자가 용적을 외부에서 건들일 수 없게 하면서 16부터 시작한 이유 중 하나다.
다른 이유는 resize() 구현에서 볼 수 있다.
[add 메소드 묶어보기]
private void linkLastNode(Node<E> o) { Node<E> last = tail; tail = o; if (last == null) { head = o; } else { o.prevLink = last; last.nextLink = o; } } public boolean add(E e) { return add(hash(e), e) == null; } private E add(int hash, E key) { int idx = hash % table.length; Node<E> newNode = new Node<E>(hash, key, null); if (table[idx] == null) { table[idx] = newNode; } else { Node<E> temp = table[idx]; Node<E> prev = null; while (temp != null) { if ((temp.hash == hash) && (temp.key == key || temp.key.equals(key))) { return key; } prev = temp; temp = temp.next; } prev.next = newNode; } size++; linkLastNode(newNode); if (size >= LOAD_FACTOR * table.length) { resize(); } return null; }
[resize 메소드 구현]
앞서 add 메소드 부터 먼저 구현을 해보았다.
resize() 메소드의 경우 결국 용적을 조정 할 대상이 table[] 노드 배열밖에 안되기 때문에 이전 HashSet과 완전히 동일하다.
그렇기에 아래 내용은 HashSet의 내용과 동일하게 갖고왔다.
항상 필자가 얘기하듯이 모든 자료구조는 동적 할당을 할 줄 알아야 한다. 만약 동적 할당이 아닌 고정 된 크기에 데이터를 넣는다면 메모리 관리도 좋지 못할 뿐더러 특히나 LinkedHashSet에서는 해시충돌을 최소화 해야하기 때문에 고정 배열크기에 데이터를 많이 추가될 수록 빠른 색인(search)이라는 HashSet의 장점을 찾아볼 수 없게 된다.
그렇기 때문에 일정 이상 데이터가 차면 배열을 늘려주어 '재배치'를 해주는 것이 당연히 성능에서 우월하다.
그리고 앞서 설명했듯이 용적 대비 데이터 개수의 비율을 부하율(load factor)라고 했고, 우리는 이 기준점을 0.75, 즉 75%을 마지노선으로 잡았다.
이 번 resize() 메소드는 크게 두 가지 방식으로 구현이 된다.
가장 보편적인 방식이 있고, 다른 하나는 용적이 만약 2^n꼴로 표현 될 경우 수학, 논리연산 지식을 조금만 응용한다면 매우 획기적으로 재배치 할 수 있는 방법이 있다.
기본적으로 resize()를 할 경우 현재 용적의 두 배로 늘려주면 된다.
일단 Node배열을 하나 새로 생성해두고, 기존 테이블에 있는 모든 요소들을 탐색하면서 각 노드의 hash값을 이용하여 새로 만든 배열의 길이로 나눈 나머지를 구해 재배치를 해주는 것이다.
일단 이미지로 한 번 보도록 하자.
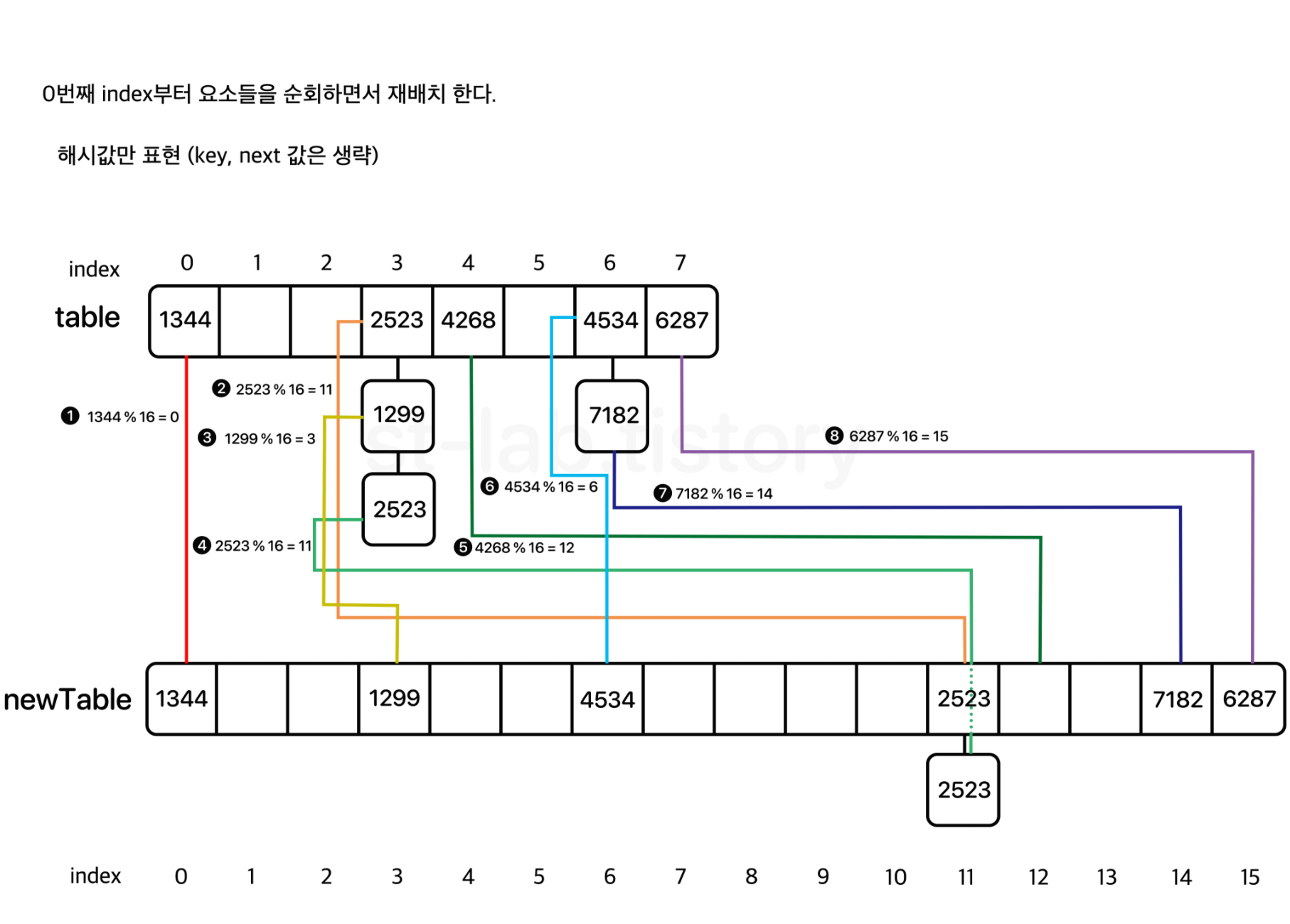
대략 위와같은 과정을 거친다고 보면 된다.
각 인덱스별로 순회하되, 해당 인덱스의 연결된 노드를 우선적으로 탐색하면서 재배치를 해주면 된다.
그럼 위 과정을 코드로 옮겨보자.
@SuppressWarnings("unchecked") private void resize() { int newCapacity = table.length * 2; // 기존 테이블의 두배 용적으로 생성 final Node<E>[] newTable = (Node<E>[]) new Node[newCapacity]; // 0번째 index부터 차례대로 순회 for (int i = 0; i < table.length; i++) { // 각 인덱스의 첫 번째 노드(head) Node<E> value = table[i]; // 해당 값이 없을 경우 다음으로 넘어간다. if (value == null) { continue; } table[i] = null; // gc Node<E> nextNode; // 현재 노드의 다음 노드를 가리키는 변수 // 현재 인덱스에 연결 된 노드들을 순회한다. while (value != null) { int idx = value.hash % newCapacity; // 새로운 인덱스를 구한다. /* * 새로 담을 index에 요소(노드)가 존재할 경우 * == 새로 담을 newTalbe에 index값이 겹칠 경우 (해시 충돌) */ if (newTable[idx] != null) { Node<E> tail = newTable[idx]; // 가장 마지막 노드로 간다. while (tail.next != null) { tail = tail.next; } /* * 반드시 value가 참조하고 있는 다음 노드와의 연결을 끊어주어야 한다. * 안하면 각 인덱스의 마지막 노드(tail)도 다른 노드를 참조하게 되어버려 * 잘못된 참조가 발생할 수 있다. */ nextNode = value.next; value.next = null; tail.next = value; } // 충돌되지 않는다면(=빈 공간이라면 해당 노드를 추가) else { /* * 반드시 value가 참조하고 있는 다음 노드와의 연결을 끊어주어야 한다. * 안하면 각 인덱스의 마지막 노드(tail)도 다른 노드를 참조하게 되어버려 * 잘못된 참조가 발생할 수 있다. */ nextNode = value.next; value.next = null; newTable[idx] = value; } value = nextNode; // 다음 노드로 이동 } } table = null; table = newTable; // 새로 생성한 table을 table변수에 연결 }
주석으로 최대한 이해하기 쉽게 설명은 해놓았다.
다만, 주의할 점이 있다면 새로운 테이블(newTable)에 변수를 담을 때 new Node<E>(value.hash, value.key, null) 이런식으로 담으면 안된다.
만약에 사용자 클래스에서 hashCode()를 오버라이드를 정확하게 해준다면 문제가 안되지만, 그러지 않고 했을 경우 기본적으로 메모리 주소에 대한 해싱 값을 반환한다고 했다.
즉, value 자체에 담고 있던 hash값과 new Node()로 생성된 새로운 노드는 내용은 같을지라도 hashCode() 값은 달라져버린다. 그렇기 때문에 value가 참조하고 있는 Node 자체를 담는 것이 안전하다.
대신에 고려해주어야 할 부분은 value를 그대로 연결시키기 떄문에 value에 연결되어있는 next 노드 또한 그대로 딸려와버리는 문제가 발생할 수 있다. 지금 재배치 되는 idx값이 다음 노드와 같다면 다행이 문제는 없겠지만, 위 이미지에서도 보았듯 같은 인덱스에 배치될 것이란 보장이 없기에 넣기 전에 미리 value.next 연결 링크를 끊고 넣어주어 정상적으로 연결되도록 하는 것이 좋다.
이미지 토대로 예시를 들자면 3번째 탐색 노드였던 1299(hash) 노드를 예로 들 수 있다.
1299(hash) 노드의 next 변수는 그 다음 노드인 2523(hash) 노드를 참조하고 있을 것이다.
1299(hash) 노드를 재배치 할 때 next 변수가 참조하고 있는 노드를 끊지 않는다면 newTable[3] 에는 1299(hash) 노드가 담기면서 그 다음 노드로 2523(hash) 노드가 같이 딸려오게 된다.
하지만 2523(hash) 노드는 newTable[11]에 배치되고 결국에는 2523(hash) 노드를 참조 하고 있는 것이 두 개(이전의 2533노드 및 1299노드)가 되어버린다는 문제가 발생한다.
즉, 이러한 문제점을 잘 파악하면서 재배치를 해주도록 한다.
[참고]
여러분이 만약 2^n 꼴로 고정된 형태의 용적을 사용 할 경우 조금의 수학적 지식을 이용한다면 매우매우 빠르고 쉽게 노드를 연결 할 수 있다.
조금만 생각해보면 우리는 각 요소들은 용적의 크기로 나눈 나머지를 이용했다. 이 말은 배열의 용적을 2배로 늘릴 때, 각 요소가 재배치 되는 인덱스는 둘 중 하나다.
음..? 왜 둘 중 하나라는 것이죠? 라고 물을 수도 있겠으니 예시를 보여주겠다.
기존 용적 : 8, 새로운 용적 : 16
9 % 8 = 1 index → 9 % 16 = 9 index
17 % 8 = 1 index → 17 % 16 = 1 index
25 % 8 = 1 index → 25 % 16 = 9 index
33 % 8 = 1 index → 33 % 16 = 1 index
보면 알겠지만, 기존 8로 나눈 나머지는 모두 1로 동일했더라도, 그 용적을 두 배로 늘리게 되면 1 또는 9, 즉 원래 자리이거나 원래 자리 + 이전 용적(1 + 8)이 된다는 것을 볼 수 있다.
다른 케이스들 또한 마찬가지다.
10 % 8 = 2 index → 10 % 16 = 10 index
18 % 8 = 2 index → 18 % 16 = 2 index
26 % 8 = 2 index → 26 % 16 = 10 index
34 % 8 = 2 index → 34 % 16 = 2 index
즉, 용적을 두 배로 늘리게 되면 두 가지 경우 중 하나에 배치된다.
1. 원래 자리(현재 자리)에 그대로 배치
2. 원래 자리에서 이전 용적을 더한 값만큼의 위치에 배치
즉, 단순하게 이미지로 보면 이렇다.
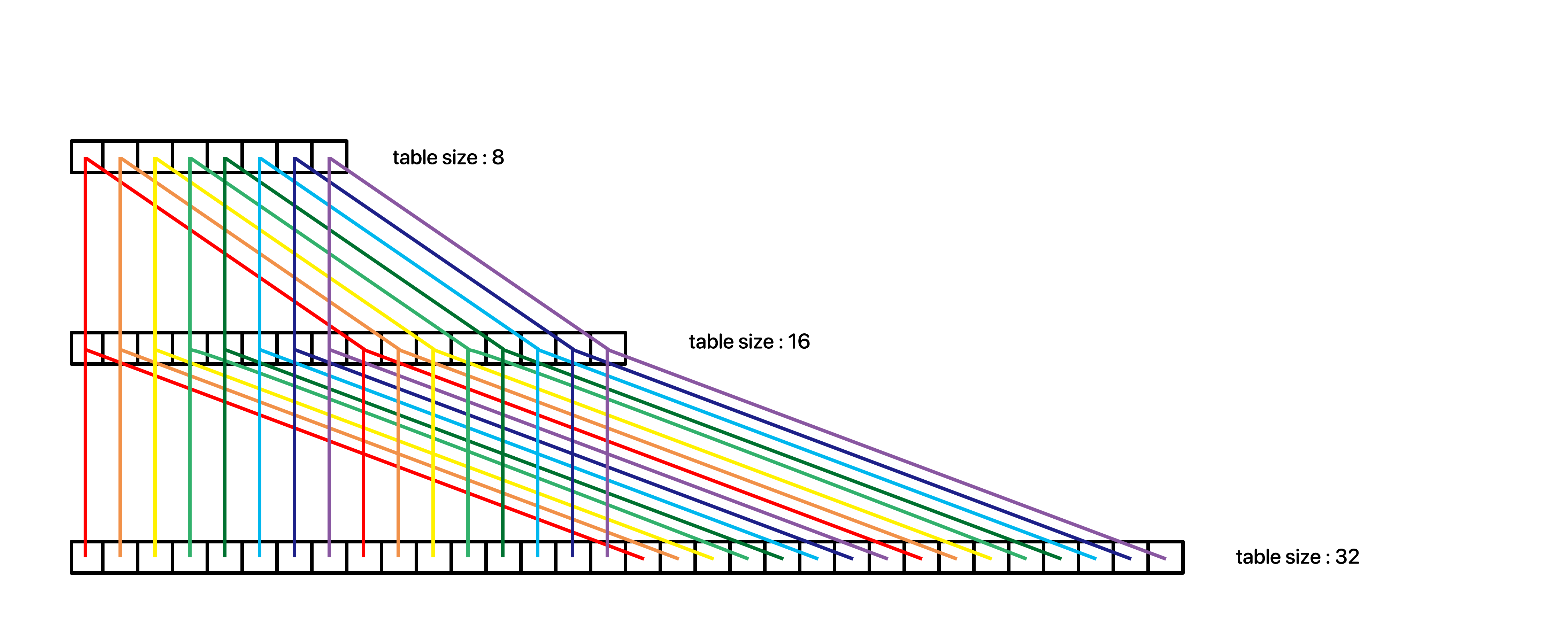
즉, 용적을 두 배 늘릴 때, 기존 인덱스는 두 개의 특정 인덱스로 위치하게 되는 것이다.
그러면 어떻게 위치를 특정해야 하는가?
맨 처음 설명했던 것 처럼 용적을 나누는 방법 (hash % capacity)이 있고, 또 다른 방법이 있다고 했다.
바로 비트 연산을 이용하는 것이다.
(이 방법은 2^n꼴에서만 유효하므로 그 외의 용적에서는 비트 연산 대신 나머지 연산으로 하시길 바란다.)
우리는 위 이미지에서 배치 되는 곳이 두 곳으로 특정된다는 것을 보았다.
이 때 재자리에 배치되는 경우(낮은 인덱스에 배치)를 low라고 하고, 재자리 + 이전 용적의 크기 값의 위치, 즉 높은 인덱스에 배치되는 경우를 high라고 나눠보자.
기존 용적 : 8, 새로운 용적 : 16
(hash % capacity)
9 % 8 = 1 index → 9 % 16 = 9 index (high)
17 % 8 = 1 index → 17 % 16 = 1 index (low)
25 % 8 = 1 index → 25 % 16 = 9 index (high)
33 % 8 = 1 index → 33 % 16 = 1 index (low)
여기서 high에 배치되는 경우는 어떨 때 일까?
바로 hash를 기존 용적으로 나눴을 때 몫이 홀수가 되는 경우다.
그럼 식이 더 복잡해지지 않나요..? 라고 반문할 수 있겠지만, 비트연산을 한다면 매우 쉽게 구할 수 있다.
2진수로 생각해보자.
8의 몫이 홀수가 된다는 것은 무슨 의미냐.
2진법을 10진법으로 변환 할 때 보통 이렇게 계산한다.
0000 1011(2) = 20 + 21 + 23 = 1 + 2 + 8 = 11
즉, 각 자리수는 2n 값인 것이다.
이 때 4를 의미한다 하면 22 (0000 0100) 이다. 그 다음 부터는 23 (0000 1000), 24 (0001 0000) ... 모두 두 배씩 증가하기 때문에 4의 짝수 배수가 된다. 이 말은 짝수 배수끼리 더해봤자 4로 나눈 몫은 항상 짝수가 나올 수 밖에 없다는 것이다.
즉, 4의 몫이 홀수가 된다는 것은 어떻던간에 세 번째 비트가 1이어야 한다는 것이다. 즉 0100 형태여야 한다는 것이다.
자 그럼 이를 예제에 적용해보자.
우리가 앞서 예시로 용적을 8에서 16으로 늘렸다.
즉, 우리가 구해야 할 것은 기존 인덱스에서 8로 나눈 몫이 짝수냐 홀수냐에 따라 high에 배치할지, low에 배치할지가 결정된다.
8을 비트로 표현하면 0000 1000 이다. 그럼 아래를 보자.
기존 용적 : 8, 새로운 용적 : 16
(hash % capacity)
9(0000 1001) % 8 = 1 index → 9 % 16 = 9 index (high)
17(0001 0001) % 8 = 1 index → 17 % 16 = 1 index (low)
25(0001 1001) % 8 = 1 index → 25 % 16 = 9 index (high)
33(0010 0001) % 8 = 1 index → 33 % 16 = 1 index (low)
보면 느낌이 오시는가?
즉, 8을 가리키는 비트가 1인지 아닌지만 판별하면 되기 때문에 결과적으로 다음과 같이 바꿔 연산할 수 있다.
(hash & oldCapacity == 0) → 기존 index 그대로 == low
(hash & oldCapacity != 0) → (기존 index + oldCapacity) == high
9(0000 1001) & 8(0000 1000) = 8(0000 1000) → 9(1 + 8) index (high)
17(0001 0001) & 8(0000 1000) = 0(0000 0000) → 1 index (low)
25(0001 1001) & 8(0000 1000) = 8(0000 1000) → 9(1 + 8) index (high)
33(0010 0001) & 8(0000 1000) = 0(0000 0000) → 1 index (low)
조금 복잡해 보일 것 같아 이미지로 앞서 재배치 하던 예시를 그대로 사용해서 보여주겠다.
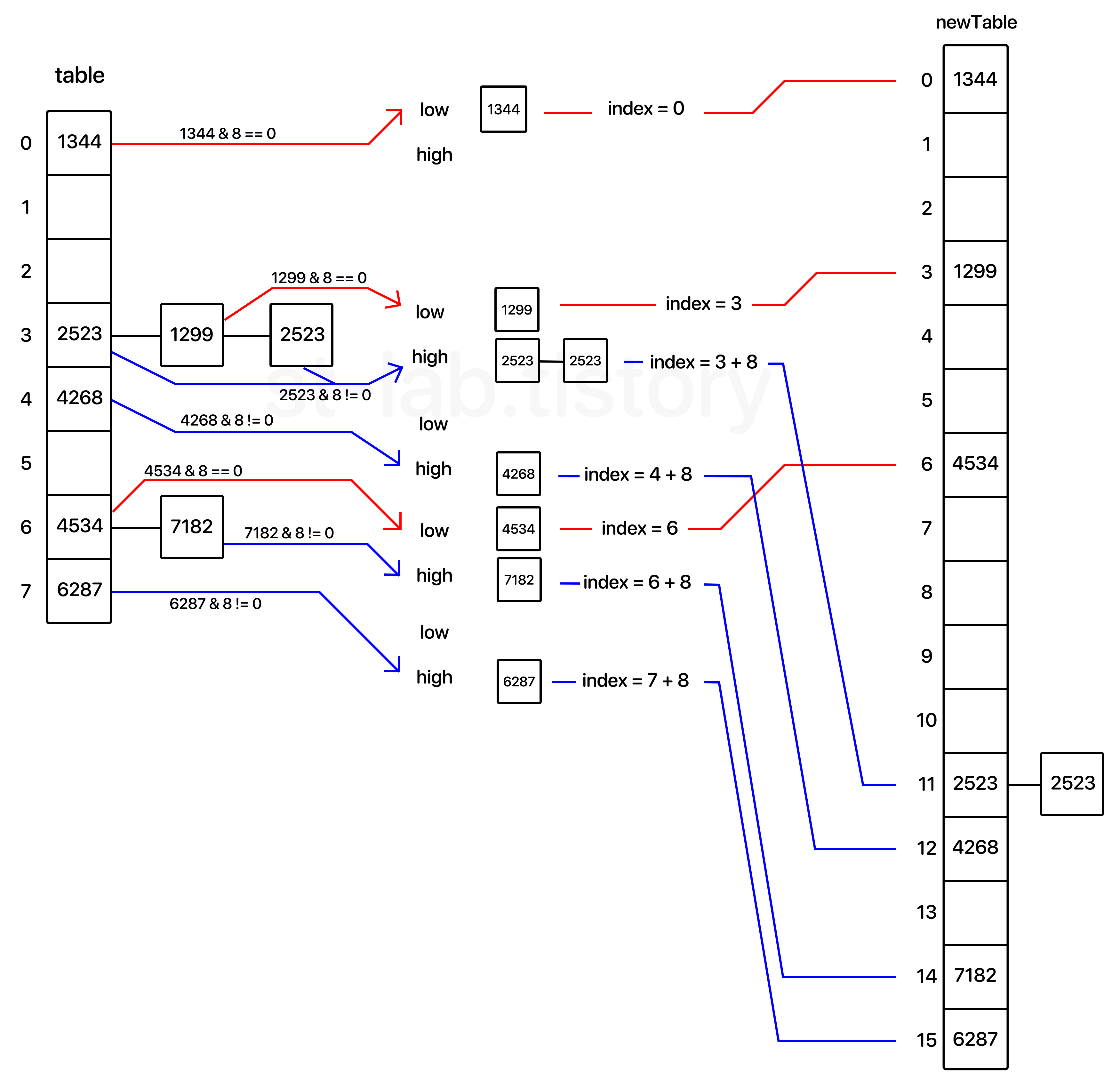
이러한 방식으로 각 인덱스별로 low와 high를 나누어 해당 노드들을 한 번에 추가하는 방법이 있다.
코드로 보면 다음과 같다.
@SuppressWarnings("unchecked") private void resize() { int oldCapacity = table.length; // 기존 용적 int newCapacity = oldCapacity << 1; // 새 용적 final Node<E>[] newTable = (Node<E>[]) new Node[newCapacity]; for(int i = 0; i < oldCapacity; i++) { Node<E> data = table[i]; if(data == null) { continue; } table[i] = null; // gc if(data.next == null) { /* * == data.hash % newCapacity * 2^n으로 000..0100..00 에서 -1을 한 0001..0011...11 꼴로 만든 뒤 * AND 연산에 의해 나머지값이 구해짐 */ newTable[data.hash & (newCapacity - 1)] = data; continue; } // 데이터가 두 개 이상 연결되어있을 경우 // 재자리 배치되는 노드(연결리스트) Node<E> lowHead = null; Node<E> lowTail = null; // 새로 배치되는 노드(연결리스트) Node<E> highHead = null; Node<E> highTail = null; /* * 재배치 되는 노드는 원래 자리에 그대로 있거나 * 원래자리에 새로 늘어난 크기만큼의 자리에 배치 되거나 둘 중 하나다. * * ex) * oldCapacity = 4, newCapacity = 8 * * 만약 데이터가 index2에 위치했다고 가정했을 때, * oldTable -> index_of_data = 2 * * 사이즈가 두 배 늘어 새로운 테이블에 배치 될 경우 두 가지 중 하나임 * newTable -> index_of_data = 2 또는 6 (2 + oldCapacity) * */ Node<E> next; // 다음 노드를 가리키는 노드 // 해당 인덱스에 연결 된 모든 노드를 탐색 do { next = data.next; // oldCapacity의 몫이 짝수일 경우 == low에 배치 됨 if((data.hash & oldCapacity) == 0) { // low에 처음 배치되는 노드일 경우 해당 노드를 head로 둔다. if(lowHead == null) { lowHead = data; } else { lowTail.next = data; } lowTail = data; // lowTail = lowTail.next와 같은 의미 } /* * data.hash & oldCapacity != 0 * * oldCapacity = 4, newCapacity = 8 일 때, * 재배치하려는 원소의 인덱스가 2라면 * * 2 또는 6에 위치하게 된다. * * 이 때, 6에 위치하는 경우라는 의미는 재배치 하기 이전의 사이즈였던 4에 대하여 * n % 4 = 2 이었을 때, n % 8 = 6이 된다는 말, * 즉, 8의 나머지에 대하여 4의 몫이 1이 된다는 말이다. * 쉽게 말하자면 4로 나눈 몫이 홀수 일 경우다. * * 비트로 생각하면 4에 대응하는 비트가 1인 경우다. * ex) * hash = 45 -> 0010 1101(2) * oldCap = 4 -> 0000 0100(2) * newCap = 8 -> 0000 1000(2) * * 재배치 이전 index = (hash & (oldCap - 1)) * 0010 1101(2) - 0000 0011(2) = 0000 0001(2) = index 1 * * 재배치 이후 index = (hash & (newCap - 1)) * 0010 1101(2) - 0000 0111(2) = 0000 0101(2) = index 5 * * 2진법으로 볼 때 새로운 위치에 배치되는 경우는 * hash & oldCap = 0010 1101(2) & 0000 0100(2) * = 0000 0100(2) 로 0이 아닌 경우다. */ else { // high에 처음 배치되는 경우 해당 노드가 head를 가리키도록 한다. if(highHead == null) { highHead = data; } else { highTail.next = data; } highTail = data; } data = next; // 다음 노드로 넘어간다. } while(data != null); /* * low 가 존재할 경우 low의 head를 원래 인덱스에 그대로 담아준다. * 이 떄 tail에 해당되는 노드가 참조하고 있는 다음 노드와의 연결을 끊어주어야 한다. * 안하면 각 인덱스의 마지막 노드(tail)도 다른 노드를 참조하게 되어버려 * 잘못된 참조가 발생할 수 있다. */ if(lowTail != null) { lowTail.next = null; newTable[i] = lowHead; } /* * high 가 존재할 경우 high의 head를 (원래 인덱스 + 이전 용적) 값에 담아준다. * 이 떄 tail에 해당되는 노드가 참조하고 있는 다음 노드와의 연결을 끊어주어야 한다. * 안하면 각 인덱스의 마지막 노드(tail)도 다른 노드를 참조하게 되어버려 * 잘못된 참조가 발생할 수 있다. */ if(highTail != null) { highTail.next = null; newTable[i + oldCapacity] = highHead; } } table = newTable; // 새 테이블을 연결해준다. }
[remove 메소드 구현]
그럼 삭제 및 반환은 어떻게 구현해야할까?
간단하다. 우리가 삽입 할 때 기존의 요소와 중복되는지를 검색했던 방식 그대로 하면 된다.
table에 해당 노드를 삭제를 해주고, 삭제된 노드와 연결 된 링크를 끊고 새로 이어줄 뿐이다.
이렇게 글로 쓰면 이해가 쉽게 되지 않을테니 한 번 그림으로 보자.
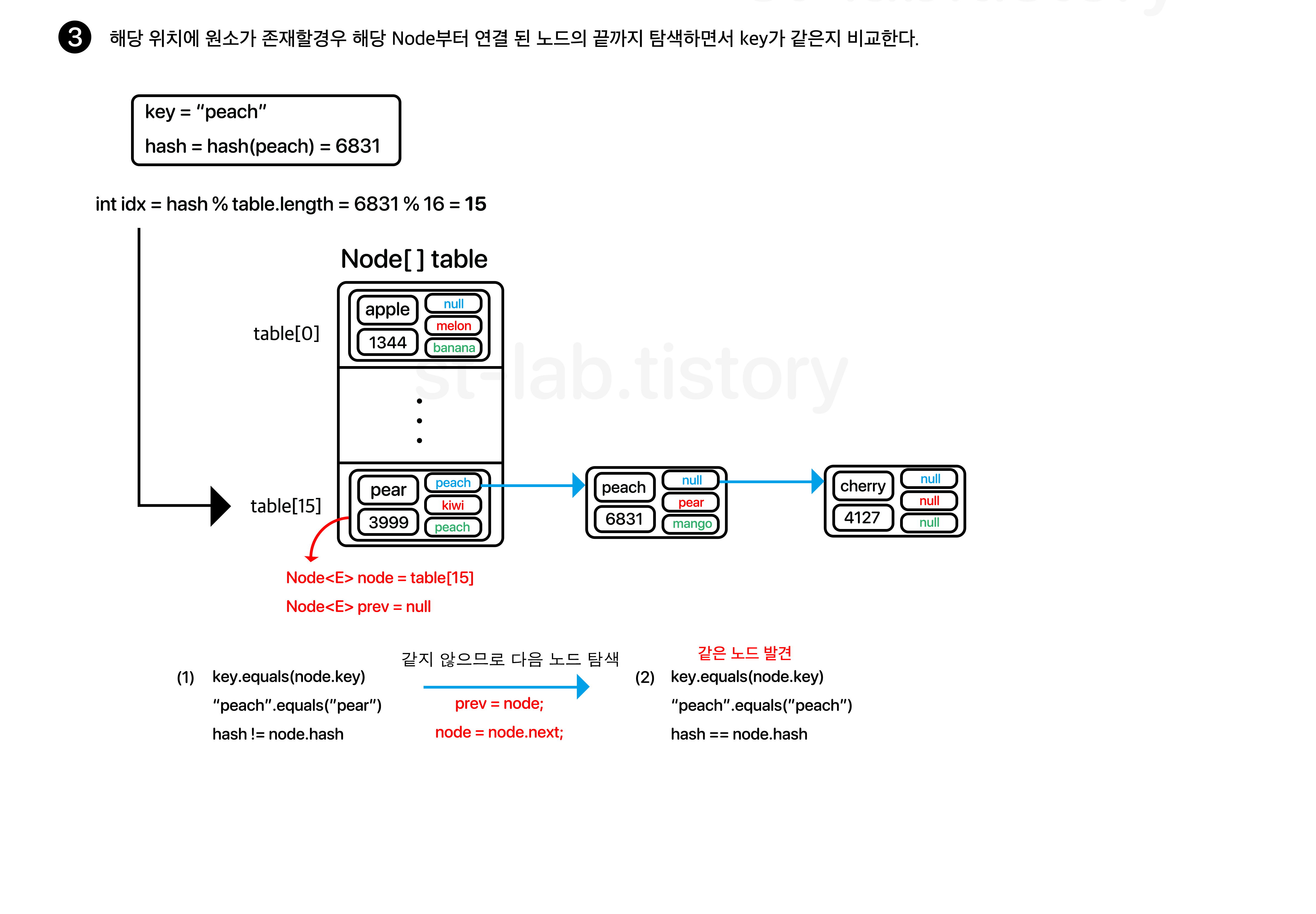
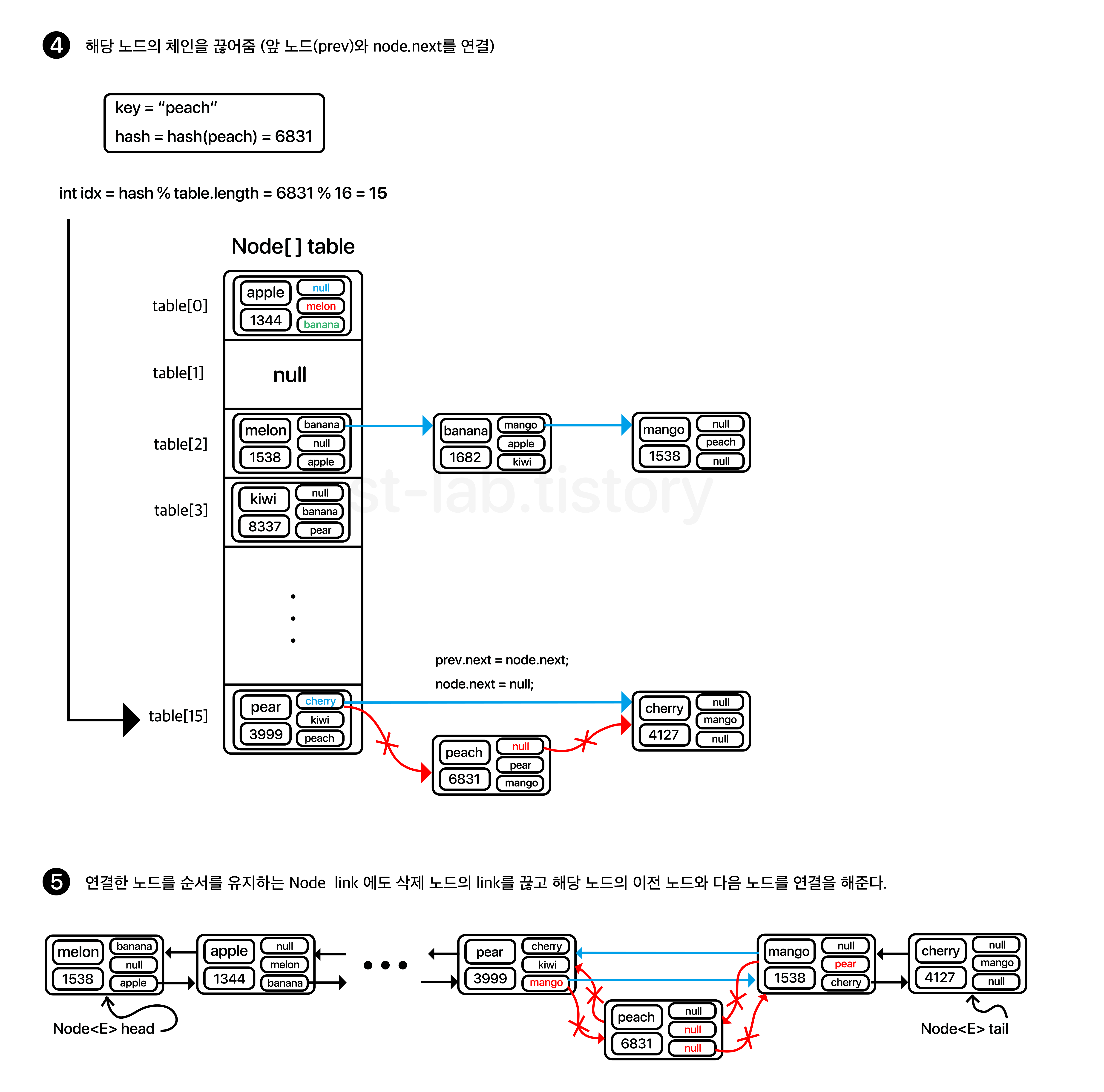
위와 같이 index를 찾고 해당 객체 내용이 같다면 해당 노드에 연결 된 링크들을 모두 끊어준 뒤, 그 앞과 뒤의 노드끼리 서로 연결해주면 된다.
그럼 이제 구현을 해보자. remove 구현 자체는 기존의 HashSet과 다를 건 없으니, 일단 연결리스트의 링크를 끊어주는 메소드부터 보도록 하자. 메소드 이름은 unlinkNode로 하겠다.
private void unlinkNode(Node<E> o) { Node<E> prevNode = o.prevLink; // 삭제하는 노드의 이전 노드 Node<E> nextNode = o.nextLink; // 삭제하는 노드의 이후 노드 /* * prevNode가 null이라는 것은 삭제한 노드가 head노드였다는 의미이므로 * 그 다음노드인 nextNode가 head가 된다. */ if (prevNode == null) { head = nextNode; } else { prevNode.nextLink = nextNode; o.prevLink = null; } /* * nextNode가 null이라는 것은 삭제한 노드가 tail이라는 의미로 * 이전 노드가 tail이 된다. */ if (nextNode == null) { tail = prevNode; } else { nextNode.prevLink = prevNode; o.nextLink = null; } }
앞, 뒤 노드를 연결하기 위해서는 위 이미지처럼 prev 변수를 하나를 두고 쓰는 것이 편리하다.
@Override public boolean remove(Object o) { // null이 아니라는 것은 노드가 삭제되었다는 의미다. return remove(hash(o), o) != null; } private Object remove(int hash, Object key) { int idx = hash % table.length; Node<E> node = table[idx]; Node<E> removedNode = null; Node<E> prev = null; if (node == null) { return null; } while (node != null) { // 같은 노드를 찾았다면 if (node.hash == hash && (node.key == key || node.key.equals(key))) { removedNode = node; // 삭제되는 노드를 반환하기 위해 담아둔다. // 해당노드의 이전 노드가 존재하지 않는 경우 (= table에 첫번째 체인 노드인 경우) if (prev == null) { table[idx] = node.next; } // 그 외엔 이전 노드의 next를 삭제할 노드의 다음노드와 연결해준다. else { prev.next = node.next; } // table의 체인을 끊었으니 다음으로 순서를 유지하는 link를 끊는다. unlinkNode(node); node = null; size--; break; // table에서 삭제되었으니 탐색 종료 } prev = node; node = node.next; } return removedNode; }
삭제 과정 위와 같이 하면 된다.
만약에 whie()문에서 같은 요소가 존재하지 않는다면 removedNode는 null 상태이므로 결국 null을 반환한다.
즉, 삭제할 노드가 없을 경우 null을 반환함으로써 상위 메소드에서 false를 반환하고, 삭제할 노드가 있을 경우 null이 아니기 때문에 true를 반환하는 원리다.
[remove 메소드 묶어보기]
private void unlinkNode(Node<E> o) { Node<E> prevNode = o.prevLink; Node<E> nextNode = o.nextLink; if (prevNode == null) { head = nextNode; } else { prevNode.nextLink = nextNode; o.prevLink = null; } if (nextNode == null) { tail = prevNode; } else { nextNode.prevLink = prevNode; o.nextLink = null; } } @Override public boolean remove(Object o) { return remove(hash(o), o) != null; } private Object remove(int hash, Object key) { int idx = hash % table.length; Node<E> node = table[idx]; Node<E> removedNode = null; Node<E> prev = null; if (node == null) { return null; } while (node != null) { if (node.hash == hash && (node.key == key || node.key.equals(key))) { removedNode = node; if (prev == null) { table[idx] = node.next; } else { prev.next = node.next; } unlinkNode(node); node = null; size--; break; } prev = node; node = node.next; } return removedNode; }
[size, isEmpty, contains, clear, equals 메소드 구현]
현재 LinkedHashSet에 저장 된 요소의 개수를 알고 싶을 때 size값을 리턴하기 위한 메소드로 size()를 하나 만들고, 해당 LinkedHashSet이 비어있는 상태인지를 확인하기 위한 isEmpty() 메소드를 만들 것이다.
또한 contains로 찾고자 하는 요소(key)가 HashSet에 존재하는지 볼 수 있도록 아주 간단하게 구현해볼 것이다. 그리고 현재 LinkedHashSet 객체와 파라미터로 주어지는 Object 객체가 같은지를 판별해주는 메소드인 equals도 작성해보도록 할 것이다.
[참고]
equals()메소드는 사실 인터페이스 Map으로 캐스팅하여(Set자체가 Map으로 구현되어있음) 서로 유사한 계열의 Set끼리도 객체 내용만 같으면 같을 수 있도록 구현되어있다. 하지만, 여기서는 LinkedHashSet으로 제한하여 구현하고자 할 것이다.
Java에서 제공하는 equals처럼 구현하려면 table의 사이즈를 알아야하는데, 그러면 Set인터페이스에 table을 두어야 한다. 문제는 가장 기본적으로 인터페이스의 멤버 변수는 상수다. 즉 변경할 수 없는 변수라 기존 LinkedHashSet의 구현 방식에 큰 지장이 생긴다.
그래서 다른 방법으로 Set 인터페이스에 Iterable 인터페이스를 extends하여 Iterator() 추상메소드를 선언한 뒤, 각 클래스 구현에서 Iterator을 구현을 해주는 방식으로 테이블에 저장 된 원소들을 순회한다.
하지만 이 방식까지 설명하기에는 글이 너무 길어지기 때문에 LinkedHashSet에 타입을 한정하여 구현할 것이다. 만약 Set 인터페이스를 구현하는 모든 클래스에 대해 비교하고싶은 경우는 필자의 깃허브에서 구현하고 있으니 참고하시길 바란다.
마지막으로 가끔 HashSet에 있는 모든 요소들을 비우고싶을 때가 있다. 그럴 때 쓸 수 있는 clear 메소드도 같이 보도록 하자.
size, isEmpty, contains, clear, equals 메소드
@Override public int size() { return size; } @Override public boolean isEmpty() { return size == 0; } @Override public boolean contains(Object o) { int idx = hash(o) % table.length; Node<E> temp = table[idx]; /* * 같은 객체 내용이어도 hash값은 다를 수 있다. * 하지만, 내용이 같은지를 알아보고 싶을 때 쓰는 메소드이기에 * hash값은 따로 비교 안해주어도 큰 지장 없다. * 단, o가 null인지는 확인해야한다. */ while (temp != null) { if (o == temp.key || (o != null && temp.key.equals(o))) { return true; } temp = temp.next; } return false; } @Override public void clear() { if (table != null && size > 0) { for (int i = 0; i < table.length; i++) { table[i] = null; } size = 0; } head = tail = null; // 마지막에 반드시 head와 tail을 끊어주어야 gc처리가 된다. } @SuppressWarnings("unchecked") @Override public boolean equals(Object o) { // 만약 파라미터 객체가 현재 객체와 동일한 객체라면 true if(o == this) { return true; } // 만약 o 객체가 LinkedHashSet 계열이 아닌경우 false if(!(o instanceof LinkedHashSet)) { return false; } LinkedHashSet<E> oSet; /* * Object로부터 LinkedHashSet<E>로 캐스팅 되어야 비교가 가능하기 때문에 * 만약 캐스팅이 불가능할 경우 ClassCastException 이 발생한다. * 이 경우 false를 return 하도록 try-catch문을 사용해준다. */ try { // LinkedHashSet 타입으로 캐스팅 oSet = (LinkedHashSet<E>) o; // 사이즈가 다르다는 것은 명백히 다른 객체다. if(oSet.size() != size) { return false; } for(int i = 0; i < oSet.table.length; i++) { Node<E> oTable = oSet.table[i]; while(oTable != null) { /* * 서로 Capacity가 다를 수 있기 때문에 index에 연결 된 원소를을 * 비교하는 것이 아닌 contains로 원소의 존재 여부를 확인해야한다. */ if(!contains(oTable)) { return false; } oTable = oTable.next; } } } catch(ClassCastException e) { return false; } // 위 검사가 모두 완료되면 같은 객체임이 증명됨 return true; }
[size, isEmpty, contains, clear, equals 메소드 묶어보기]
@Override public int size() { return size; } @Override public boolean isEmpty() { return size == 0; } @Override public boolean contains(Object o) { int idx = hash(o) % table.length; Node<E> temp = table[idx]; while (temp != null) { if (o == temp.key || (o != null && temp.key.equals(o))) { return true; } temp = temp.next; } return false; } @Override public void clear() { if (table != null && size > 0) { for (int i = 0; i < table.length; i++) { table[i] = null; } size = 0; } head = tail = null; } @SuppressWarnings("unchecked") @Override public boolean equals(Object o) { if(o == this) { return true; } if(!(o instanceof LinkedHashSet)) { return false; } LinkedHashSet<E> oSet; try { // LinkedHashSet 타입으로 캐스팅 oSet = (LinkedHashSet<E>) o; // 사이즈가 다르다는 것은 명백히 다른 객체다. if(oSet.size() != size) { return false; } for(int i = 0; i < oSet.table.length; i++) { Node<E> oTable = oSet.table[i]; while(oTable != null) { if(!contains(oTable)) { return false; } oTable = oTable.next; } } } catch(ClassCastException e) { return false; } return true; }
[toArray 메소드 구현]
LinkedHashSet의 link를 하는 목적이 보이는 중요한 메소드다.
그동안의 자료구조에서는 이 부분은 굳이 구현하는데 중요한 부분은 아니라 넘어가도 됐다. 다만 조금 더 많은 기능을 원할 경우 추가해주면 좋은 메소드로 넘어갔지만 이 번에는 LinkedHashSet에 있는 데이터들을 모두 얻고자 할 때, 특히 들어온 순서대로 유지하기 위해 해당 메소드를 사용 할 수 있다. (HashSet은 table 순회 방식으로 데이터 순서 유지가 안되었다.)
1. toArray() 메소드
toArray()는 크게 두 가지가 있다.
하나는 아무런 인자 없이 현재 있는 LinkedHashSet 요소들을 객체배열(Object[]) 로 반환해주는 Object[] toArray() 메소드가 있고, 다른 하나는 LinkedHashSet을 이미 생성 된 다른 배열에 복사해주고자 할 때 쓰는 T[] toArray(T[] a) 메소드가 있다.
즉 차이는 이런 것이다.
LinkedHashSet<Integer> hashset = new LinkedHashSet<>(); // get LinkedHashSet to array (using toArray()) Object[] s1 = hashset.toArray(); // get LinkedHashSet to array (using toArray(T[] a) Integer[] s2 = new Integer[10]; s2 = hashset.toArray(s2);
1번의 장점이라면 LinkedHashSet에 있는 요소의 수만큼 정확하게 배열의 크기가 할당되어 반환된다는 점이다.
2번의 장점이라면 객체 클래스로 상속관계에 있는 타입이거나 Wrapper(Integer -> int) 같이 데이터 타입을 유연하게 캐스팅할 여지가 있다는 것이다.
우리가 SinglyLinkedList나 DoublyLInkedList의 toArray() 처럼 요소 순회를 head를 통해 순서대로 데이터를 저장하여 반환하면 된다.
두 메소드 모두 구현해보자면 다음과 같다.
public Object[] toArray() { if (table == null || head == null) { return null; } Object[] ret = new Object[size]; int index = 0; // 들어온 순서대로 head부터 tail까지 순회한다. for(Node<E> x = head; x != null; x = x.nextLink) { ret[index] = x.key; index++; } return ret; } @SuppressWarnings("unchecked") public <T> T[] toArray(T[] a) { Object[] copy = toArray(); if (a.length < size) { return (T[]) Arrays.copyOf(copy, size, a.getClass()); } System.arraycopy(copy, 0, a, 0, size); return a; }
먼저 두 번째 toArray(T[] a) 의 경우 첫 번째 toArray() 로 보내도록 하겠다. (동작 구현이 겹치기 때문이다.)
첫 번째 toArray() 구현 자체는 어렵지 않을 것이다.
그리고 두 번째 toArray(T[] a) 의 경우
그러면 크게 두 가지로 나누어 볼 수 있다.
하나는 a 배열이 현재 LinkedHashSet에 담긴 요소보다 작은 사이즈일 경우다. 그럴 때는 Arrays 클래스의 copyOf()메소드를 활용하면 된다.
copyOf() 메소드에 대한 자세한 내용은 아래를 보면 된다.
Arrays (Java SE 11 & JDK 11 )
Compares two int arrays lexicographically over the specified ranges. If the two arrays, over the specified ranges, share a common prefix then the lexicographic comparison is the result of comparing two elements, as if by Integer.compare(int, int), at a rel
docs.oracle.com
쉽게 말하면 이렇다.
copyOf(원본 배열, 복사할 길이, 반환 될 배열 클래스(타입))
그 외에는 LinkedHashSet 요소 개수보다 a 배열이 더 큰 경우이므로, LinkedHashSet의 첫 번째 인덱스부터 size 위치까지의 요소를 a 배열에 0번째 인덱스부터 복사해주면 된다.
이는 System.arraycopy() 메소드를 써주면 된다.
System (Java SE 11 & JDK 11 )
Determines the current system properties. First, if there is a security manager, its checkPropertiesAccess method is called with no arguments. This may result in a security exception. The current set of system properties for use by the getProperty(String)
docs.oracle.com
[toArray 메소드 묶어보기]
public Object[] toArray() { if (table == null || head == null) { return null; } Object[] ret = new Object[size]; int index = 0; for(Node<E> x = head; x != null; x = x.nextLink) { ret[index] = x.key; index++; } return ret; } @SuppressWarnings("unchecked") public <T> T[] toArray(T[] a) { Object[] copy = toArray(); if (a.length < size) { return (T[]) Arrays.copyOf(copy, size, a.getClass()); } System.arraycopy(copy, 0, a, 0, size); return a; }
- 전체 코드
import java.util.Arrays; import Interface_form.Set; public class LinkedHashSet<E> implements Set<E>{ // 최소 기본 용적이며 2^n꼴 형태가 좋다. private final static int DEFAULT_CAPACITY = 1 << 4; // 3/4 이상 채워질 경우 resize하기 위한 임계값 private static final float LOAD_FACTOR = 0.75f; Node<E>[] table; // 요소의 정보를 담고있는 Node를 저장할 Node타입 배열 private int size; // 요소의 개수 // 들어온 순서를 유지할 linkedlist private Node<E> head; // 노드의 첫 부분 private Node<E> tail; // 노드의 마지막 부분 @SuppressWarnings("unchecked") public LinkedHashSet() { table = (Node<E>[]) new Node[DEFAULT_CAPACITY]; size = 0; head = null; tail = null; } // 보조 해시 함수 (상속 방지를 위해 private static final 선언) private static final int hash(Object key) { int hash; if (key == null) { return 0; } else { // hashCode()의 경우 음수가 나올 수 있으므로 절댓값을 통해 양수로 변환해준다. return Math.abs(hash = key.hashCode()) ^ (hash >>> 16); } } @SuppressWarnings("unchecked") private void resize() { int newCapacity = table.length * 2; // 기존 테이블의 두배 용적으로 생성 final Node<E>[] newTable = (Node<E>[]) new Node[newCapacity]; // 0번째 index부터 차례대로 순회 for (int i = 0; i < table.length; i++) { // 각 인덱스의 첫 번째 노드(head) Node<E> value = table[i]; // 해당 값이 없을 경우 다음으로 넘어간다. if (value == null) { continue; } table[i] = null; // gc Node<E> nextNode; // 현재 노드의 다음 노드를 가리키는 변수 // 현재 인덱스에 연결 된 노드들을 순회한다. while (value != null) { int idx = value.hash % newCapacity; // 새로운 인덱스를 구한다. /* * 새로 담을 index에 요소(노드)가 존재할 경우 * == 새로 담을 newTalbe에 index값이 겹칠 경우 (해시 충돌) */ if (newTable[idx] != null) { Node<E> tail = newTable[idx]; // 가장 마지막 노드로 간다. while (tail.next != null) { tail = tail.next; } /* * 반드시 value가 참조하고 있는 다음 노드와의 연결을 끊어주어야 한다. * 안하면 각 인덱스의 마지막 노드(tail)도 다른 노드를 참조하게 되어버려 * 잘못된 참조가 발생할 수 있다. */ nextNode = value.next; value.next = null; tail.next = value; } // 충돌되지 않는다면(=빈 공간이라면 해당 노드를 추가) else { /* * 반드시 value가 참조하고 있는 다음 노드와의 연결을 끊어주어야 한다. * 안하면 각 인덱스의 마지막 노드(tail)도 다른 노드를 참조하게 되어버려 * 잘못된 참조가 발생할 수 있다. */ nextNode = value.next; value.next = null; newTable[idx] = value; } value = nextNode; // 다음 노드로 이동 } } table = null; table = newTable; // 새로 생성한 table을 table변수에 연결 } private void linkLastNode(Node<E> o) { Node<E> last = tail; // 마지막 노드를 갖고온다. tail = o; // tail을 새로운 노드 o가 가리키도록 갱신해준다. /* * 만약 마지막 노드가 null이라는 것은 노드에 저장된 데이터가 없는, * 즉 head 노드도 null인 상태라는 것이다. * 그러므로 head도 새 노드인 o를 가리키도록 한다. */ if (last == null) { head = o; } /* * last가 null이 아닐경우 새 노드 o의 앞의 노드를 가리키는 노드를 last로 두고, * last의 다음 노드는 새 노드인 o를 가리키도록 한다. */ else { o.prevLink = last; last.nextLink = o; } } @Override public boolean add(E e) { return add(hash(e), e) == null; } private E add(int hash, E key) { int idx = hash % table.length; Node<E> newNode = new Node<E>(hash, key, null); // 새로운 노드 if (table[idx] == null) { table[idx] = newNode; } else { Node<E> temp = table[idx]; Node<E> prev = null; while (temp != null) { if ((temp.hash == hash) && (temp.key == key || temp.key.equals(key))) { return key; } prev = temp; temp = temp.next; } prev.next = newNode; } size++; linkLastNode(newNode); // table에 저장이 끝났으면 해당 노드를 연결해준다. // 데이터의 개수가 현재 table 용적의 75%을 넘어가는 경우 용적을 늘려준다. if (size >= LOAD_FACTOR * table.length) { resize(); } return null; } private void unlinkNode(Node<E> o) { Node<E> prevNode = o.prevLink; // 삭제하는 노드의 이전 노드 Node<E> nextNode = o.nextLink; // 삭제하는 노드의 이후 노드 /* * prevNode가 null이라는 것은 삭제한 노드가 head노드였다는 의미이므로 * 그 다음노드인 nextNode가 head가 된다. */ if (prevNode == null) { head = nextNode; } else { prevNode.nextLink = nextNode; o.prevLink = null; } /* * nextNode가 null이라는 것은 삭제한 노드가 tail이라는 의미로 * 이전 노드가 tail이 된다. */ if (nextNode == null) { tail = prevNode; } else { nextNode.prevLink = prevNode; o.nextLink = null; } } @Override public boolean remove(Object o) { // null이 아니라는 것은 노드가 삭제되었다는 의미다. return remove(hash(o), o) != null; } private Object remove(int hash, Object key) { int idx = hash % table.length; Node<E> node = table[idx]; Node<E> removedNode = null; Node<E> prev = null; if (node == null) { return null; } while (node != null) { // 같은 노드를 찾았다면 if (node.hash == hash && (node.key == key || node.key.equals(key))) { removedNode = node; // 삭제되는 노드를 반환하기 위해 담아둔다. // 해당노드의 이전 노드가 존재하지 않는 경우 (= table에 첫번째 체인 노드인 경우) if (prev == null) { table[idx] = node.next; } // 그 외엔 이전 노드의 next를 삭제할 노드의 다음노드와 연결해준다. else { prev.next = node.next; } // table의 체인을 끊었으니 다음으로 순서를 유지하는 link를 끊는다. unlinkNode(node); node = null; size--; break; // table에서 삭제되었으니 탐색 종료 } prev = node; node = node.next; } return removedNode; } @Override public int size() { return size; } @Override public boolean isEmpty() { return size == 0; } @Override public boolean contains(Object o) { int idx = hash(o) % table.length; Node<E> temp = table[idx]; /* * 같은 객체 내용이어도 hash값은 다를 수 있다. * 하지만, 내용이 같은지를 알아보고 싶을 때 쓰는 메소드이기에 * hash값은 따로 비교 안해주어도 큰 지장 없다. * 단, o가 null인지는 확인해야한다. */ while (temp != null) { if (o == temp.key || (o != null && temp.key.equals(o))) { return true; } temp = temp.next; } return false; } @Override public void clear() { if (table != null && size > 0) { for (int i = 0; i < table.length; i++) { table[i] = null; } size = 0; } head = tail = null; // 마지막에 반드시 head와 tail을 끊어주어야 gc처리가 된다. } @SuppressWarnings("unchecked") @Override public boolean equals(Object o) { // 만약 파라미터 객체가 현재 객체와 동일한 객체라면 true if(o == this) { return true; } // 만약 o 객체가 LinkedHashSet 계열이 아닌경우 false if(!(o instanceof LinkedHashSet)) { return false; } LinkedHashSet<E> oSet; /* * Object로부터 LinkedHashSet<E>로 캐스팅 되어야 비교가 가능하기 때문에 * 만약 캐스팅이 불가능할 경우 ClassCastException 이 발생한다. * 이 경우 false를 return 하도록 try-catch문을 사용해준다. */ try { // LinkedHashSet 타입으로 캐스팅 oSet = (LinkedHashSet<E>) o; // 사이즈가 다르다는 것은 명백히 다른 객체다. if(oSet.size() != size) { return false; } for(int i = 0; i < oSet.table.length; i++) { Node<E> oTable = oSet.table[i]; while(oTable != null) { /* * 서로 Capacity가 다를 수 있기 때문에 index에 연결 된 원소를을 * 비교하는 것이 아닌 contains로 원소의 존재 여부를 확인해야한다. */ if(!contains(oTable)) { return false; } oTable = oTable.next; } } } catch(ClassCastException e) { return false; } // 위 검사가 모두 완료되면 같은 객체임이 증명됨 return true; } public Object[] toArray() { if (table == null || head == null) { return null; } Object[] ret = new Object[size]; int index = 0; // 들어온 순서대로 head부터 tail까지 순회한다. for(Node<E> x = head; x != null; x = x.nextLink) { ret[index] = x.key; index++; } return ret; } @SuppressWarnings("unchecked") public <T> T[] toArray(T[] a) { Object[] copy = toArray(); if (a.length < size) { return (T[]) Arrays.copyOf(copy, size, a.getClass()); } System.arraycopy(copy, 0, a, 0, size); return a; } }
위 코드는 아래 깃허브에서도 소스 코드를 편리하게 보실 수 있다. 또한 깃허브에 올라가는 코드들은 조금 더 기능을 추가하거나 수정되어 올라가기에 약간의 차이는 있을 수 있지만 전체적인 구조는 바뀌지 않으니 궁금하시거나 참고하실 분들은 아래 링크로 가서 보시는 걸 추천한다.
[소스코드 모아보기]
kdgyun/Data_Structure
Contribute to kdgyun/Data_Structure development by creating an account on GitHub.
github.com
- 정리
이 번에는 만약 이전 HashSet 구현을 보고왔다면 그리 어렵지 않았을 것이다.
개념 자체가 HashSet 기능에 순서를 유지하는 link만 더 추가하여 연결해준 것이기 때문에 기본적인 자료구조 지식을 갖고 그동안 하나씩 구현해보았다면 금방 구현했을 것이다.
참고로 만약 사용자 클래스를 사용하고자 한다면 반드시 hashCode()와 equals를 재정의(Override)하셔야 한다. 그래야 객체가 동일한지 아닌지를 정확하게 비교할 수 있다.
그렇지 않을 경우 같은 내용을 담고 있을지라도 new로 생성된 객체들은 모두 서로다른 객체로 hashCode()가 달리 나오기 때문이다.
그리고 가장 중요한 것, 바로 순서가 유지되는지 한 번 확인해보자.
public class test { public static void main(String[] args) { LinkedHashSet<Integer> s = new LinkedHashSet<Integer>(); s.add(71); s.add(36); s.add(44); s.add(12); s.add(96); s.add(38); s.add(17); s.add(48); s.add(20); s.add(77); // 테이블에 저장 된 데이터 System.out.println("[테이블 순회]"); for(int i = 0; i < s.table.length; i++) { System.out.print("index " + i + " : "); Node<Integer> v = s.table[i]; if(v == null) { System.out.print("null"); } while(v != null) { System.out.print(v.key + " "); v = v.next; } System.out.println(); } // 연결 순서가 유지되는 데이터 System.out.print("\n순서 유지 : "); Object[] a = s.toArray(); for(Object v : a) { System.out.print(v + " "); } } }
(구현 패키지와 같은 곳에 test를 한 것이라 table에 접근이 가능하다.)
위와 같이 table에 저장 되어있는 상태와, 실제로 우리가 사용할 때 toArray()같은 방식으로 데이터를 얻어서 출력하면 어떤 차이가 있는지 확인 할 수 있다.
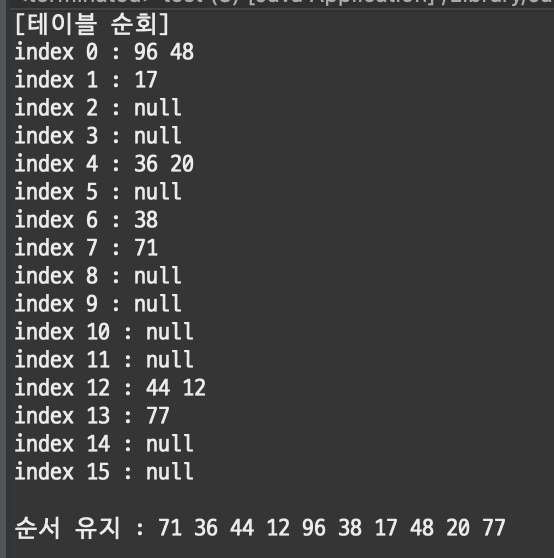
보면 테이블에 저장 된 방식은 순서가 유지되지 않지만, 각 노드들은 순서를 유지하도록 link를 하기때문에 뽑아올 땐 순서가 유지가 되는 것을 볼 수 있다.
이렇게 LinkedHashSet을 구현해보았는데 당연히 어려울 수 있다. 혹여 이해가 안되는 부분, 또는 질문이 있다면 언제든 댓글을 남겨주시면 된다. 최대한 빠르게 답변드리겠다.
'자료구조 > Java' 카테고리의 다른 글
| 자바 [JAVA] - Binary Search Tree (이진 탐색 트리) 구현하기 (13) | 2022.09.24 |
|---|---|
| 자바 [JAVA] - Hash Set (해시 셋) 구현하기 (14) | 2021.04.14 |
| 자바 [JAVA] - Set Interface (셋 인터페이스) (0) | 2021.04.09 |
| 자바 [JAVA] - Priority Queue (우선순위 큐) 구현하기 (24) | 2021.03.04 |
| 자바 [JAVA] - 배열을 이용한 Heap (힙) 구현하기 (52) | 2021.02.10 |
댓글을 사용할 수 없습니다.