[백준] 10757번 : 큰 수 A+B - JAVA [자바]
10757번: 큰 수 A+B
두 정수 A와 B를 입력받은 다음, A+B를 출력하는 프로그램을 작성하시오.
www.acmicpc.net
- 문제

Java로 풀 경우 매우 쉽게 풀 수 있는 문제다.
- 알고리즘 [접근 방법]
참고로 일반적으로 큰 수를 쓸 때 쓰는 long형은 264-1으로 약 1844경 정도 된다.
하지만 이 번 문제의 경우 입력 범위가 최대 1010000 이므로 long형을 아득히 넘는다.
그러면 이를 어떻게 풀어야 할까?
크게 두 가지 방식이 있다.
먼저 덧셈 과정을 직접 구현하는 방법이 있다. 그리고 Java에서 제공하는 BIgInteger 클래스를 이용하는 방법이 있다.
이 번에는 이 두 방식 모두 보여주려고 한다.
먼저 덧셈을 구현하는 방식이다.
가장 간단한 방식은 각각 입력받은 수를 배열로 나타내어 서로를 더하는 것이다. 덧셈 과정을 생각해보자. 우리가 어릴 때 배웠던 덧셈 과정을 생각해보면 다음과 같다.
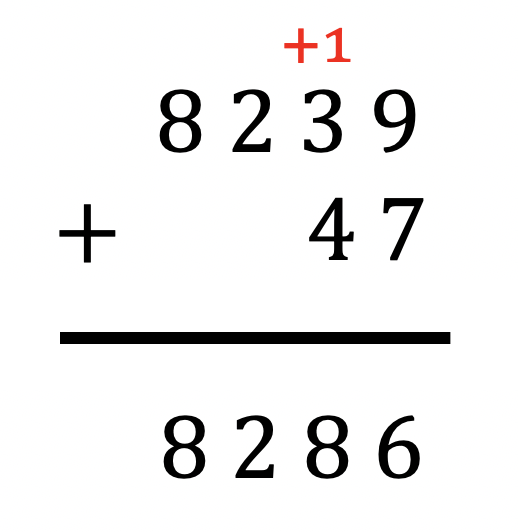
즉, 가장 낮은 자리 수부터 덧셈을 하며, 10이 넘어가면 다음 자리값에 +1을 해준다.
근데, 만약 받은 숫자를 배열로 채울 때 각 자릿값을 앞(왼쪽)에서 부터 채우게 되면 이런 엉뚱한 결과가 발생할 수 있다.

즉, 이렇게 되지 않도록 배열에 채울 때는 앞 인덱스(index)에 1의 자리수부터 채워나가야 좀 더 편하게 코드를 짤 수 있다.
또한, 배열의 인덱스는 각 자리수를 의미하기 때문에 만약 두 수의 각 자리값을 더해서 나온 결과가 10이 넘을 수가 있다.
그렇기 때문에 각 자리는 10으로 나눈 '나머지 값'을 저장해야 하며, 10이 넘었을 때는 올림이 발생했다는 의미이므로 '다음 자리수'에 +1을 해주어야 한다.
위 예시를 그림으로 보자면 다음과 같다.

그리고 위 구조를 코드로 옮기면 다음과 같이 된다.
String str_A = input();
String str_B = input();
int max_length = max(str_A.length(), str_B.length());
int[] A = new int[max_length + 1]; // 마지막 자리수 올림이 있을 수 있으므로 +1
int[] B = new int[max_length + 1]; // 마지막 자리수 올림이 있을 수 있으므로 +1
// A 초기화
for(int i = A.length - 1, int idx = 0; i >= 0; i--, idx++) {
A[idx] = str_A.charAt(i) - '0'; // 맨 뒤 문자부터 역순으로 하나씩 저장
}
// B 초기화
for(int i = B.length - 1, int idx = 0; i >= 0; i--, idx++) {
B[idx] = str_B.charAt(i) - '0'; // 맨 뒤 문자부터 역순으로 하나씩 저장
}
// 덧셈
for(int i = 0; i < max_length; i++) {
int value = A[i] + B[i];
A[i] = value % 10; // 더한 값의 10으로 나눈 나머지가 자리값이 됨
A[i + 1] = A[i + 1] + (value / 10); // 더한 값의 10으로 나눈 몫이 올림값이 됨
}
// A배열 역순 출력
// 가장 높은 자리수가 0일 수도 있기 때문에 0이 아닐 경우에만 출력
if(A[max_length] != 0) {
print(A[max_length]);
}
for(int i = max_length - 1; i >= 0; i--) {
print(A[i]);
}
이런 과정을 거치면 된다.
물론 위와같이 구현 할 수도 있고, 다른 방법으로는 BigInteger 클래스를 사용할 수도 있다.
보통 long형이 넘어가는 매우 큰 수에 대해서 사용하게 되는데, 자세한 API는 다음 링크를 보면 된다.
docs.oracle.com/javase/8/docs/api/java/math/BigInteger.html
BigInteger (Java Platform SE 8 )
Immutable arbitrary-precision integers. All operations behave as if BigIntegers were represented in two's-complement notation (like Java's primitive integer types). BigInteger provides analogues to all of Java's primitive integer operators, and all relevan
docs.oracle.com
클래스 객체이기 때문에 당연히 선언 및 생성을 해주어야 하고, 생성할 때 파라미터로 "문자열"을 넘겨주어야 한다.
BigInteger A = new BigInteger(input());
BigInteger B = new BigInteger(input());
/*
* add() 메소드는 해당 BigInteger 객체와 파라미터(인자)로 들어온
* BigInteger객체의 더한 값을 BigInteger 타입으로 반환한다.
*/
A = A.add(B);
print(A.toString());
이를 토대로 이제 출력과 몇 가지 소스만 만들어주면 된다.
- 4가지 방법을 사용하여 풀이한다.
알고리즘을 두 개 설명했다. 직접 구현 방식과 기존에 Java에서 제공하는 BigInteger 클래스를 이용하는 방식. 이 두 개와 각 방식에 대해 입력방법을 달리하여 성능의 차이를 보고자 한다.
즉, 다음과 같이 네 가지의 방식을 살펴보고자 한다.
1. Scanner + 직접구현
2. Scanner + BigInteger
3. BufferedReader + 직접구현
4. BufferedReader + BigInteger
- 풀이
- 방법 1 : [Scanner + 직접구현]
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String str_A = in.next();
String str_B = in.next();
// 두 개의 수 중 가장 긴 자리수 길이를 구해둠
int max_length = Math.max(str_A.length(), str_B.length());
int[] A = new int[max_length + 1]; // 마지막 자리수 올림이 있을 수 있으므로 +1
int[] B = new int[max_length + 1]; // 마지막 자리수 올림이 있을 수 있으므로 +1
// A 초기화
for(int i = str_A.length() - 1, idx = 0; i >= 0; i--, idx++) {
A[idx] = str_A.charAt(i) - '0'; // 맨 뒤 문자부터 역순으로 하나씩 저장
}
// B 초기화
for(int i = str_B.length() - 1, idx = 0; i >= 0; i--, idx++) {
B[idx] = str_B.charAt(i) - '0'; // 맨 뒤 문자부터 역순으로 하나씩 저장
}
// 덧셈
for(int i = 0; i < max_length; i++) {
int value = A[i] + B[i];
A[i] = value % 10; // 더한 값의 10으로 나눈 나머지가 자리값이 됨
A[i + 1] += (value / 10); // 더한 값의 10으로 나눈 몫이 올림값이 됨
}
// A배열 역순 출력
// 가장 높은 자리수가 0일 수도 있기 때문에 0이 아닐 경우에만 출력
StringBuilder sb = new StringBuilder();
if(A[max_length] != 0) {
sb.append(A[max_length]);
}
for(int i = max_length - 1; i >= 0; i--) {
sb.append(A[i]);
}
System.out.println(sb);
}
}
가장 기본적인 방법이라 할 수 있겠다.
참고로 모든 출력은 StringBuilder 로 통일했다. 워낙 자리수가 크기 때문에 하나하나씩 출력하는 것은 매우 비효율적이기 때문.
- 방법 2 : [Scanner + BigInteger]
BigInteger 클래스를 사용하는 방법이다. 참고로 BigInteger는 java.math 패키지에 존재한다.
import java.util.Scanner;
import java.math.BigInteger;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
BigInteger A = new BigInteger(in.next());
BigInteger B = new BigInteger(in.next());
A = A.add(B);
System.out.println(A.toString());
}
}
크게 어려울 것은 없을 것이다. 엄청 코드가 간단해진 것을 볼 수 있다.
- 방법 3 : [BufferedReader + 직접구현]
입력 방법을 Scanner 대신 BufferedReader 을 사용하면서 직접 덧셈을 구현하는 방법이다. 단, BufferedReader 는 문자열을 한 줄로 읽기 때문에 A과 B을 구분하기 위해 공백을 기준으로 문자열을 분리해주어야하니 StringTokenizer 을 사용하여 풀도록 하겠다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
String str_A = st.nextToken();
String str_B = st.nextToken();
// 두 개의 수 중 가장 긴 자리수 길이를 구해둠
int max_length = Math.max(str_A.length(), str_B.length());
int[] A = new int[max_length + 1]; // 마지막 자리수 올림이 있을 수 있으므로 +1
int[] B = new int[max_length + 1]; // 마지막 자리수 올림이 있을 수 있으므로 +1
// A 초기화
for(int i = str_A.length() - 1, idx = 0; i >= 0; i--, idx++) {
A[idx] = str_A.charAt(i) - '0'; // 맨 뒤 문자부터 역순으로 하나씩 저장
}
// B 초기화
for(int i = str_B.length() - 1, idx = 0; i >= 0; i--, idx++) {
B[idx] = str_B.charAt(i) - '0'; // 맨 뒤 문자부터 역순으로 하나씩 저장
}
for(int i = 0; i < max_length; i++) {
int value = A[i] + B[i];
A[i] = value % 10; // 더한 값의 10으로 나눈 나머지가 자리값이 됨
A[i + 1] += (value / 10); // 더한 값의 10으로 나눈 몫이 올림값이 됨
}
// A배열 역순 출력
// 가장 높은 자리수가 0일 수도 있기 때문에 0이 아닐 경우에만 출력
StringBuilder sb = new StringBuilder();
if(A[max_length] != 0) {
sb.append(A[max_length]);
}
for(int i = max_length - 1; i >= 0; i--) {
sb.append(A[i]);
}
System.out.println(sb);
}
}
- 방법 4 : [BufferedReader + BigInteger]
방법 2에서 Scanner 대신 BufferedReader 을 사용하여 풀이하는 방법이다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
import java.math.BigInteger;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
BigInteger A = new BigInteger(st.nextToken());
BigInteger B = new BigInteger(st.nextToken());
A = A.add(B);
System.out.println(A.toString());
}
}
- 성능

채점 번호 : 25920698 - 방법 4 : BufferedReader + BigInteger
채점 번호 : 25920686 - 방법 3 : BufferedReader + 직접구현
채점 번호 : 25920669 - 방법 2 : Scanner + BigInteger
채점 번호 : 25920656 - 방법 1 : Scanner + 직접구현
입력의 경우는 확실히 Scanner 보다는 BufferedReader 가 빠른 걸 볼 수 있다.
또한 BigInteger 클래스는 아무래도 문자열 검사, 음수, 양수 검사 등 거쳐야하는 과정이 많기 때문에 그렇다.
- 정리
이 번 문제 또한 어려운 점은 없었을 것이다. 보통은 구현의 귀찮음 때문에 Java의 경우 BigInteger로 쉽게 풀이할 수 있지만, C, C++의경우 직접 구현하거나, 사용자 라이브러리를 갖고와서 써야하기 때문에 알고리즘 문제인만큼 한 번 직접 과정을 구현해보는 것을 추천한다.
'JAVA - 백준 [BAEK JOON] > 기본 수학 1' 카테고리의 다른 글
| [백준] 2775번 : 부녀회장이 될테야 - JAVA [자바] (27) | 2020.04.05 |
|---|---|
| [백준] 10250번 : ACM 호텔 - JAVA [자바] (12) | 2020.04.04 |
| [백준] 2869번 : 달팽이는 올라가고 싶다 - JAVA [자바] (38) | 2020.04.01 |
| [백준] 1193번 : 분수찾기 - JAVA [자바] (41) | 2020.03.31 |
| [백준] 2292번 : 벌집 - JAVA [자바] (17) | 2020.03.29 |