[백준] 2579번 : 계단 오르기 - JAVA [자바]
2579번: 계단 오르기
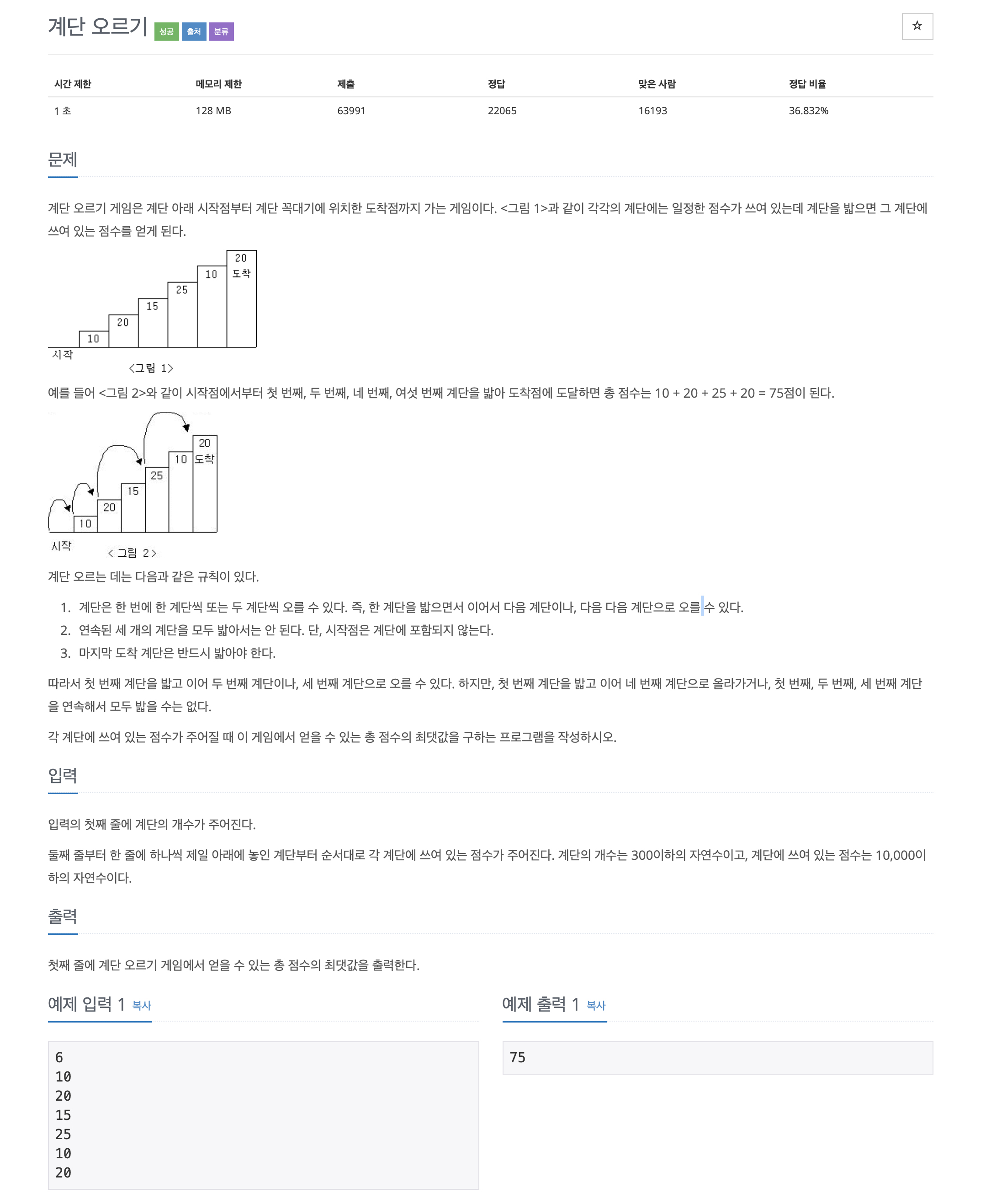
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점
www.acmicpc.net
-
문제
생각보다 많은 분들이 틀렸던 문제다. 특히 문제 조건을 제대로 이해하지 못하거나 동적계획법을 제대로 이해하지 못해 틀리는 경우가 대다수였던 것 같다. 조건들을 유의하면서 풀어야 하니 차근차근 알아보자.
- 알고리즘 [접근 방법]
문제는 어렵지 않다. 문제에서 나온 것처럼 크게 다음과 같은 세 가지 조건을 만족해야한다.
1. 계단을 오를 때 한 계단, 또는 두 계단을 오를 수 있다.
2. 연속된 3개의 계단을 밟으면 안된다. (즉, 한 계단씩 올라갈 때 최대 연속으로 2번만 한계단씩 오를 수 있다는 의미다.)
3. 마지막 계단은 '반드시' 밟아야 한다.
생각보다 이 문제를 재귀로 풀어내지 못하는 분들이 많았다. 만약 필자의 동적계획법 포스팅들을 봤다면 쉽게 이해할 수 있으리라 생각하지만, 혹시 모르니 다시 한 번 자세하게 살펴보도록 하자.
그동안 필자가 풀이 방법을 Top-Down 방식, 즉 큰 문제부터 작은문제로 들어가는 방식이였다. 이 때 재귀호출을 통해 작은문제로 쪼개서 들어가는 것. 이 것이 Top-Down 방식이다. Top-Down방식이 있다면 당연히 그 반대인 Bottom-UP 방식도 있다. Bottom-UP 방식은 작은문제부터 풀어가며 전체 문제를 풀어가는 방식이다. 이 방법은 대개 반복문을 통해 구현된다.
그럼 두 가지 방식 모두 살펴보도록 하자. 우리가 동적계획법을 짤 때 주의해야 할 점이 있다. Memoization(메모이제이션)을 할 때 이전에 계산한 값을 저장할텐데 이번 문제는 연속으로 3계단을 밟을 수 없다. 그렇기 때문에 잘못 재귀호출 하면 모든 계단이 더해지거나 이를 초과한 값이 나오는 등 우리가 원하는 값과는 엉뚱한 값을 받을 수 있다.
기본적인 알고리즘은 이렇다.
static int find(int N) {
if(dp[N] == null) {
dp[N] = Math.max(find(N - 2), find(N - 3) + arr[N - 1]) + arr[N];
}
return dp[N];
}
여기서 다른 점이 보이는가? 재귀호출을 할 때 N-2 와 N-3 은 재귀호출을 하지만 N-1 은 재귀호출을 하지 않는다.
잘 생각해보자. N-1 값을 재귀호출 한다면 어떻게 될까? 만약 N=5라고 한다면 N=4, N= 3,... 해서 dp[N]이 null이 아닐 때 까지, 즉 메모이제이션이 아닐 때까지 호출된다. find(N-1)을 호출하여 N = 5 값을 넣었다고 가정하면 DP[4] 이 메모이제이션이 되어있다고 할 때 이전 계단(N-3)을 밟은 상태인지 알 수 있는가? 알 수 없다. 그렇기 때문에 이에 대한 해결 방법으로는 연속 된 블럭의 경우의 수는 재귀호출이 아니라 이미 입력받은 배열의 값을 더해주어야 한다.
한 마디로 두 계단 전의 경우와(N-2) 와 직전 계단을 밟고(N-1) 그 이전에는 두 계단 이전의 경우(N-3)에서 연속되지 않는 위치인 N-2와 N-3에 대해서만 재귀호출을 해주어야 한다. (아마 이 부분에서 많이 틀리신 것 같다.)
Bottom-Up 방법도 마찬가지다. 계단 1층부터 하나씩 값을 더해가면서 채워나가 마지막 계단에서 누적 된 합을 구하면 되는데 DP[i-1]을 누적합을 구하는데 사용한다면 위 재귀와 마찬가지로 올바른 결과가 나오지 않는다.
즉, 현재 인덱스 i 에 대해 두 칸 전(i - 2)의 '메모이제이션 값'과 첫 칸 전(i - 1)의 값 + 셋 째칸 전(i - 3)의 '메모이제이션 값' 중 큰 값을 현재 i 계단의 값과 합하여 DP배열에 저장(Memoization)을 해주면 된다.
쉽게 말하면 다음과 같이 반복문으로 짤 수 있다.
for (int i = 3; i <= N; i++) {
DP[i] = Math.max(DP[i - 2] , DP[i - 3] + arr[i - 1]) + arr[i];
}
이 때 주의할 점은 i - 3, 세 번째 칸 이전 것의 값을 찾을 때 i가 3 미만의 수라면 음수로 참조할 수 없는 인덱스에 접근하게 된다. ArrayIndexOutOfBoundsException 가 뜬다는 말이다.
초기화까지 코드로 넣는다면 아래와 같다.
[재귀 : Top-Down]
// 재귀 dp는 int[] 배열이 아닌 Integer[] 객체배열을 쓸 것이다.
dp[0] = arr[0];
dp[1] = arr[1];
// N 이 1이 입력될 수도 있기 때문에 예외처리를 해줄 필요가 있다.
if (N >= 2) {
DP[2] = arr[1] + arr[2];
}
static int find(int N) {
if(dp[N] == null) {
dp[N] = Math.max(find(N - 2), find(N - 3) + arr[N - 1]) + arr[N];
}
return dp[N];
}
[반복문 : Bottom - Up]
/*
반복문 DP배열은 int[] 배열로 쓸 것이기 때문에
index 0은 초기화해줄 필요 없다.
*/
DP[1] = arr[1];
// N 이 1이 입력될 수도 있기 때문에 예외처리를 해줄 필요가 있다.
if (N >= 2) {
DP[2] = arr[1] + arr[2];
}
for (int i = 3; i <= N; i++) {
DP[i] = Math.max(DP[i - 2] , DP[i - 3] + arr[i - 1]) + arr[i];
}
나머지는 코드를 보면서 설명하도록 하겠다.
- 4가지 방법을 사용하여 풀이한다.
위에서 설명한 두 가지 방식인 Top-Down 과 Bottom-Up을 토대로 각 알고리즘별 입력을 달리하여 성능을 비교하고자 한다. 정리하자면 다음 네 가지 방식을 보여주려한다.
1 . 재귀(Top-Down) + Scanner
2. 재귀(Top-Down) + BufferedReader
3. 반복문(Bottom-Up) + Scanner
4. 반복문(Bottom-Up) + BufferedReader
- 풀이
- 방법 1 : [재귀(Top-Down) + Scanner]
import java.util.Scanner;
public class Main {
static Integer dp[];
static int arr[];
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
dp = new Integer[N + 1];
arr = new int[N + 1];
for(int i = 1; i <= N; i++) {
arr[i] = in.nextInt();
}
dp[0] = arr[0]; // 디폴트값이 null이므로 0으로 초기화 해주어야한다.
dp[1] = arr[1];
if(N >= 2) {
dp[2] = arr[1] + arr[2];
}
System.out.println(find(N));
}
static int find(int N) {
// 아직 탐색하지 않는 N번째 계단일 경우
if(dp[N] == null) {
dp[N] = Math.max(find(N - 2), find(N - 3) + arr[N - 1]) + arr[N];
}
return dp[N];
}
}
가장 기본적인 방법이라 할 수 있겠다. 큰 문제를 호출하여 작은 문제로 호출하여 풀어나가는 방식을 Top-Down 방식이라 한다.
- 방법 2 : [재귀(Top-Down) + BufferedReader]
입력 방법을 Scanner 대신 BufferedReader 을 사용하여 풀이하는 방법이다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
static Integer dp[];
static int arr[];
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
dp = new Integer[N + 1];
arr = new int[N + 1];
for(int i = 1; i <= N; i++) {
arr[i] = Integer.parseInt(br.readLine());
}
dp[0] = arr[0]; // 디폴트값이 null이므로 0으로 초기화 해주어야한다.
dp[1] = arr[1];
if(N >= 2) {
dp[2] = arr[1] + arr[2];
}
System.out.println(find(N));
}
static int find(int N) {
// 아직 탐색하지 않는 N번째 계단일 경우
if(dp[N] == null) {
dp[N] = Math.max(find(N - 2), find(N - 3) + arr[N - 1]) + arr[N];
}
return dp[N];
}
}
아마 재귀로 구현하는 것에 익숙치 않은 분들은 이해가 잘 안될 수도 있다. 만약 그렇다면 직적 그림으로 그려가면서 하나씩 처리해보자. 그래도 이해가 안되면 댓글을 남겨주시길 바란다.
- 방법 3 : [반복문(Bottom-Up) + Scanner]
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
int[] DP = new int[N + 1];
int[] arr = new int[N + 1];
for (int i = 1; i <= N; i++) {
arr[i] =in.nextInt();
}
// index = 0 은 시작점이므로 0이다.
DP[1] = arr[1];
// N 이 1이 입력될 수도 있기 때문에 예외처리를 해줄 필요가 있다.
if (N >= 2) {
DP[2] = arr[1] + arr[2];
}
for (int i = 3; i <= N; i++) {
DP[i] = Math.max(DP[i - 2] , DP[i - 3] + arr[i - 1]) + arr[i];
}
System.out.println(DP[N]);
}
}
아마 대부분은 이러한 방식이 가장 쉽게 느낄 것 같다. 이렇게 작은 문제부터 풀어나가는 방식을 Bottom-Up 방식이라 한다. (대부분 for문으로 구현됨)
- 방법 4 : [반복문(Bottom-Up) + BufferedReader]
입력 방법을 Scanner 대신 BufferedReader 을 사용하여 풀이하는 방법이다. 아마 필자가 알기로는 자바 제출자 중 이 방법으로 푼 사람이 대부분인 것 같다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[] DP = new int[N + 1];
int[] arr = new int[N + 1];
for (int i = 1; i <= N; i++) {
arr[i] = Integer.parseInt(br.readLine());
}
// index = 0 은 시작점이다.
DP[1] = arr[1];
// N 이 1이 입력될 수도 있기 때문에 예외처리를 해줄 필요가 있다.
if (N >= 2) {
DP[2] = arr[1] + arr[2];
}
for (int i = 3; i <= N; i++) {
DP[i] = Math.max(DP[i - 2] , DP[i - 3] + arr[i - 1]) + arr[i];
}
System.out.println(DP[N]);
}
}
음.. 별달리 설명할 것이 없다.
- 성능

채점 번호 : 22092428 - 방법 4 : 반복문(Bottom-Up) + BufferedReader
채점 번호 : 22092422 - 방법 3 : 반복문(Bottom-Up) + Scanner
채점 번호 : 22092418 - 방법 2 : 재귀(Top-Down) + BufferedReader
채점 번호 : 22092409 - 방법 1 : 재귀(Top-Down) + Scanner
알고리즘상으로는 차이가 거의 없다.
입력의 경우는 확실히 Scanner 보다는 BufferedReader 가 빠른 걸 볼 수 있다.
- 정리
문제 자체가 어렵다기보다는 함정이 숨어있는 문제였다. 아마 문제 자체가 그렇게 노리고 만들어진 것 같았고, 많은 분들도 여기에 속은 것 같다.
오늘은 이전과는 달리 두 가지 알고리즘으로 나누어 풀었는데, 두 방식 모두 장단점이 있는데 재귀의 경우 점화식을 그대로 가져다가 쓸 수 있어 설계가 쉬운 대신 메모리나 시간이 반복문에 비해 무겁다는게 단점이고 반복문의 경우 메모리나 시간측면에서 일반적으로 재귀에 비해 빠르나, 그래프같은 복잡한 자료구조에 동적계획법을 적용한다면 설계할 것이 늘어난다.
쉽게 생각하면 문제를 '분해'하느냐, '결합'하느냐의 차이다.
만약 문제나 풀이가 이해가 안된다면 댓글에 남겨주시면 된다. 최대한 빠르게 답변드리도록 하겠다.
'JAVA - 백준 [BAEK JOON] > 동적 계획법 1' 카테고리의 다른 글
| [백준] 10844번 : 쉬운 계단 수 - JAVA [자바] (46) | 2020.08.29 |
|---|---|
| [백준] 1463번 : 1로 만들기 - JAVA [자바] (36) | 2020.08.28 |
| [백준] 1932번 : 정수 삼각형 - JAVA [자바] (17) | 2020.08.26 |
| [백준] 1149번 : RGB거리 - JAVA[자바] (18) | 2020.08.11 |
| [백준] 9461번 : 파도반 수열 - JAVA [자바] (11) | 2020.08.05 |