[백준] 2231번 : 분해합 - JAVA [자바]
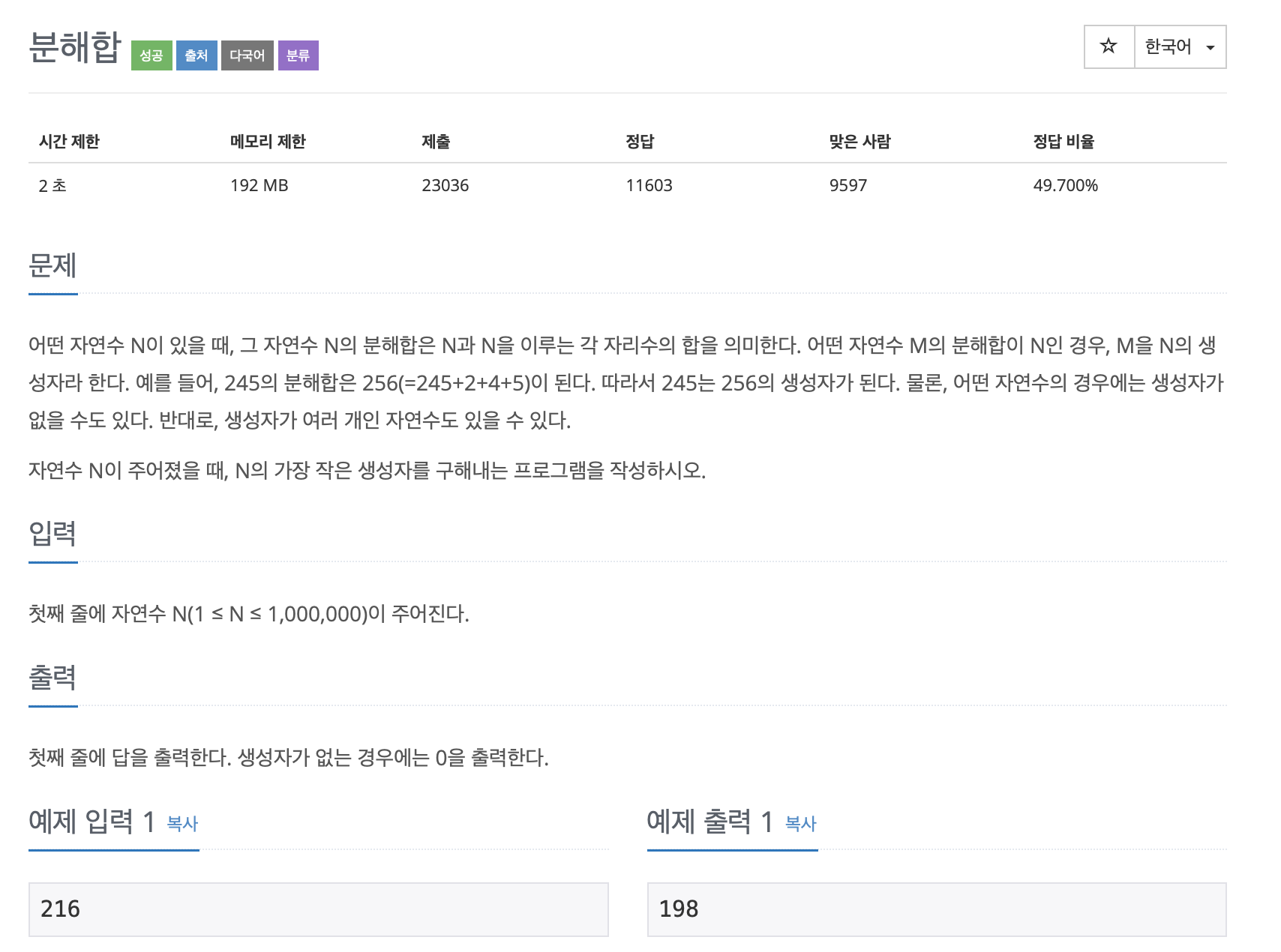
2231번: 분해합
문제 어떤 자연수 N이 있을 때, 그 자연수 N의 분해합은 N과 N을 이루는 각 자리수의 합을 의미한다. 어떤 자연수 M의 분해합이 N인 경우, M을 N의 생성자라 한다. 예를 들어, 245의 분해합은 256(=245+2+
www.acmicpc.net
- 문제
이번 문제도 브루트포스를 이용하여 푸는 문제다!
- 알고리즘 [접근방법]
문제가 그리 어렵지 않다.
198 = 198 + 1 + 9 + 8 = 216
예로들어 198 이라는 생성자가 주어졌을 때 198 의 분해합은 198 + 1 + 9 + 8 = 216 이다.
반대로 216 의 생성자는 여러가지가 있다.
예로들어 앞선 예제처럼 198 이 될 수도 있고 207 이 될 수도 있다.
즉, 생성자의 경우에는 1개 이상이기 때문에 최솟값을 찾기 위해서는 작은 수 부터 찾아야한다는 것을 알 수 있다.
가장 기본적인 방법은 1 부터 입력받은 N 까지 한 개씩 모두 대입해보는 것이다.
이게 가장 기본적인 브루트포스 방식이다.
만약 탐색 도중 생성자를 찾으면 종료하고 해당 생성자를 출력하며, N 을 넘길 때 까지 생성자를 찾지 못하면 0을 출력하면 된다.
간략하게 코드로 짜면 다음과 같을 것이다.
for(int i = 0; i < N; i++) {
int number = i;
int sum = 0; // 각 자릿수 합 변수
while(number != 0) {
sum += number % 10; // 각 자릿수 더하기
number /= 10;
}
// i 값과 각 자릿수 누적합이 같을 경우 (생성자를 찾았을 경우)
if(sum + i == N) {
result = i;
break;
}
}
여기에 조금 더 응용한 방법은 다음과 같다.
어떤 임의의 수 N이 들어올 때, 해당 수 N 은 K + K의 각 자릿수 합이다.
예로들어 네자릿수 정수 N 이 들어오면 해당 N 을 만드는 생성자는 임의의 K + K의 각 자릿수가 되는 것이다.
즉, 수식으로 보면 다음과 같다.
N(4) = K + k1 + k2 + k3 + k4
그리고 이항을 하면 다음과 같다.
N(4) - (k1 + k2 + k3 + k4) = K
즉, 네자릿수 N 의 각 자릿수의 합이 최대일 때는 언제인가?
9 + 9 + 9 + 9 일 것이다.
즉, 우리는 입력받은 정수 N 에 대하여 자릿수의 길이만큼 9를 빼주면 된다.
그 미만의 수는 생성자가 될 수 없다는 것은 자명하다는 것이다.
정리하자면
N - (9 × K의 길이) 부터 탐색하여 N 까지만 탐색하면 된다.
코드로 보자면 다음과 같을 것이다.
// i 는 가능한 최솟값인 N - 9 * N의 각 자릿수부터 시작
for(int i = (N - (N_length * 9)); i < N; i++) {
int number = i;
int sum = 0; // 각 자릿수 합 변수
while(number != 0) {
sum += number % 10; // 각 자릿수 더하기
number /= 10;
}
// i 값과 각 자릿수 누적합이 같을 경우 (생성자를 찾았을 경우)
if(sum + i == N) {
result = i;
break;
}
}
위와같이 두 가지 방법으로 접근 할 수 있다.
- 4가지 방법을 이용하여 풀이한다.
앞서 설명한 두 가지 알고리즘을 비교해보고자 한다.
그리고 각 알고리즘별로 입력방법을 달리하여 풀어본다.
입력은 Scanner 와 BufferedReader 을 통한 방법으로 보여줄 것이다.
- 풀이
- 방법 1
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
int result = 0;
for(int i = 0; i < N; i++) {
int number = i;
int sum = 0; // 각 자릿수 합 변수
while(number != 0) {
sum += number % 10; // 각 자릿수 더하기
number /= 10;
}
// i 값과 각 자릿수 누적합이 같을 경우 (생성자를 찾았을 경우)
if(sum + i == N) {
result = i;
break;
}
}
System.out.println(result);
}
}
가장 기본적인 방법이라 할 수 있겠다.
0 부터해서 N 이전까지 만족하는 값을 찾기 전까지는 계속 탐색하는 방법이다.
- 방법 2
방법 1 에서 Scanner 대신 BufferedReader 을 사용하는 방법이다.
알고리즘은 0 부터 N 직전까지 탐색하는 방법이다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int result = 0;
for(int i = 0; i < N; i++) {
int number = i;
int sum = 0; // 각 자릿수 합 변수
while(number != 0) {
sum += number % 10; // 각 자릿수 더하기
number /= 10;
}
// i 값과 각 자릿수 누적합이 같을 경우 (생성자를 찾았을 경우)
if(sum + i == N) {
result = i;
break;
}
}
System.out.println(result);
}
}
- 방법 3
좀 더 응용한 알고리즘(N - 자릿수 * 9 부터 시작)을 사용한 방법이다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 자릿수의 길이를 알기위해 일단 문자열로 입력받는다.
String str_N = in.nextLine();
// 해당 문자열의 길이 변수
int N_len = str_N.length();
// 문자열을 정수(int)로 변환
int N = Integer.parseInt(str_N);
int result = 0;
// i 는 가능한 최솟값인 N - 9 * N의 각 자릿수부터 시작
for(int i = (N - (N_len * 9)); i < N; i++) {
int number = i;
int sum = 0; // 각 자릿수 합 변수
while(number != 0) {
sum += number % 10; // 각 자릿수 더하기
number /= 10;
}
// i 값과 각 자릿수 누적합이 같을 경우 (생성자를 찾았을 경우)
if(sum + i == N) {
result = i;
break;
}
}
System.out.println(result);
}
}
아무래도 탐색 범위가 좁아진 만큼 성능은 더 좋을 것이다.
- 방법 4
방법 3 의 Scanner 대신 BufferedReader 을 사용한 방법이다.
알고리즘 자체는 동일하다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 자릿수의 길이를 알기위해 일단 문자열로 입력받는다.
String str_N = br.readLine();
// 해당 문자열의 길이 변수
int N_len = str_N.length();
// 문자열을 정수(int)로 변환
int N = Integer.parseInt(str_N);
int result = 0;
// i 는 가능한 최솟값인 N - 9 * N의 각 자릿수부터 시작
for(int i = (N - (N_len * 9)); i < N; i++) {
int number = i;
int sum = 0; // 각 자릿수 합 변수
while(number != 0) {
sum += number % 10; // 각 자릿수 더하기
number /= 10;
}
// i 값과 각 자릿수 누적합이 같을 경우 (생성자를 찾았을 경우)
if(sum + i == N) {
result = i;
break;
}
}
System.out.println(result);
}
}
- 성능

위에서 부터 순서대로
채점 번호 : 19919085 - 방법 4 : BufferedReader
채점 번호 : 19919083 - 방법 3 : Scanner
채점 번호 : 19919080 - 방법 2 : BufferedReader
채점 번호 : 19919075 - 방법 1 : Scanner
입력의 경우 확실히 Scanner 보다는 BufferedReader 가 빠르고
탐색 범위를 좁히니 시간이 더욱 단축되는 것을 볼 수 있다.
- 정리
다들 브루트 포스 문제는 그렇게 어렵지 않게 풀 수 있을 것이다.
그냥 완전탐색 알고리즘만 만들고 만족하는 값을 찾을 때 까지 돌리면 되기 때문이다.
다만 같은 브루트 포스 알고리즘이라도 자명하게 불가능한 범위를 제외시키면 성능을 더욱 향상시킬 수 있으니, 이러한 부분에서 고민을 해보는 과정을 거치면 좋을 것 같다.
'JAVA - 백준 [BAEK JOON] > 브루트 포스' 카테고리의 다른 글
| [백준] 1436번 : 영화감독 숌 - JAVA [자바] (89) | 2020.05.27 |
|---|---|
| [백준] 1018번 : 체스판 다시 칠하기 - JAVA [자바] (52) | 2020.05.26 |
| [백준] 7568번 : 덩치 - JAVA [자바] (20) | 2020.05.21 |
| [백준] 2798번 : 블랙잭 - JAVA [자바] (15) | 2020.05.19 |