[백준] 1002번 : 터렛 - JAVA [자바]
https://www.acmicpc.net/problem/1002
1002번: 터렛
각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.
www.acmicpc.net
- 문제
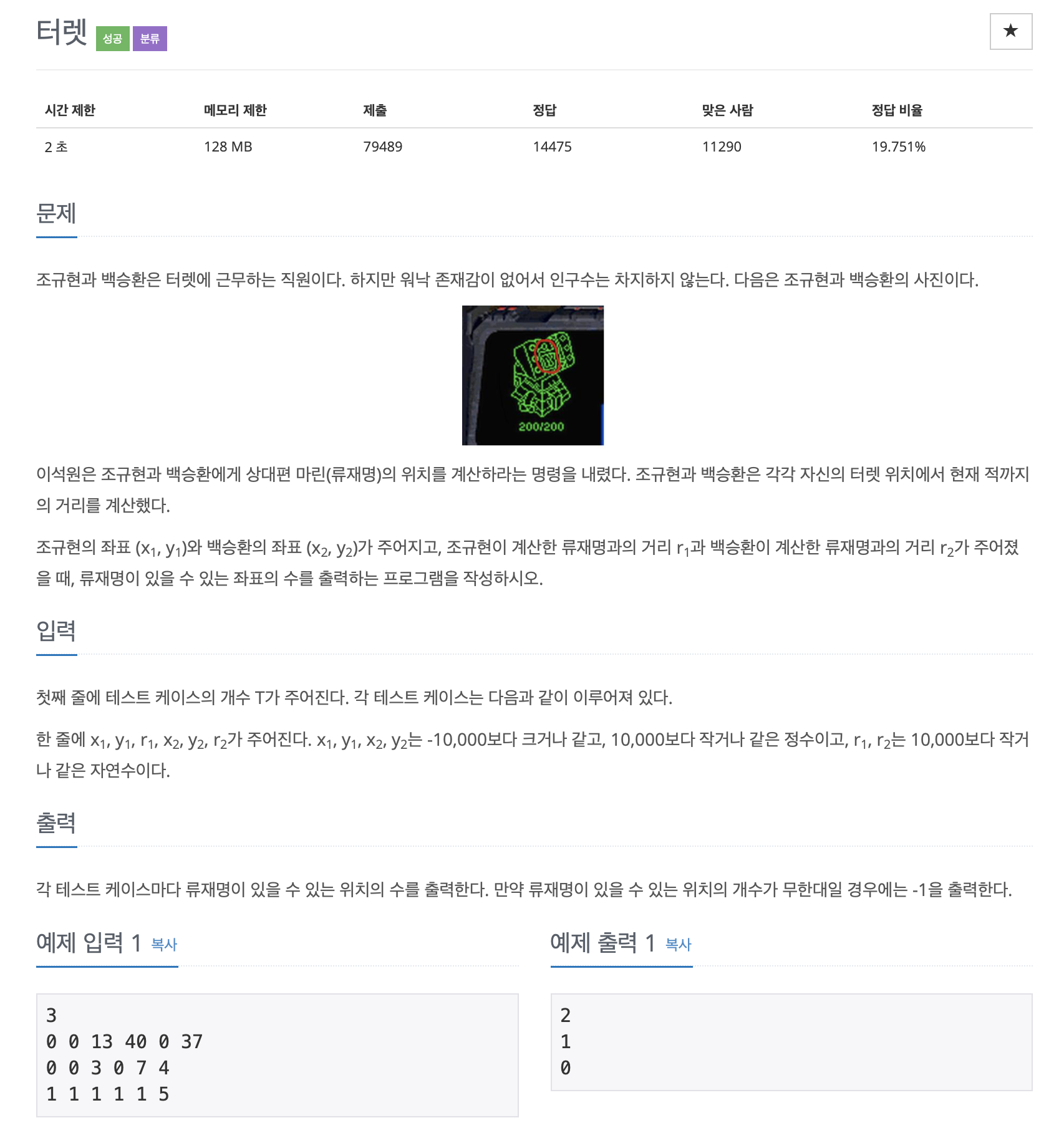
필자가 처음 문제를 볼 때 뭔 말인가 싶었다..
그래도 이해만 한다면 매우매우 쉬운 문제이니 차근차근 풀어보자.
- 알고리즘 [풀이 방법]
일단 문제부터 이해해보자.
문제에서의 조규현과 백승환을 각각 A, B 라고 한다면 더 이해하기 쉽다.
좌표상에서 A터렛의 위치 (𝑥₁, 𝑦₁) 가 주어지고, B터렛의 위치 (𝑥₂, 𝑦₂) 가 주어진다.
그리고 마린(류재명)을 C라고 할 때,
A 와 B가 자신의 위치로부터의 거리를 각각 계산한 것이다.
즉, A로부터 C까지의 거리가 𝑟₁ 이고,
B로부터 C까지의 거리가 𝑟₂ 라는 것이다.
그렇게 𝑥₁, 𝑦₁, 𝑟₁, 𝑥₂, 𝑦₂, 𝑟₂ 가 주어졌을 때 C가 있을 수 있는 위치의 수를 찾으라는 것이다.
그림으로 생각하자면 다음과 같다.
각 터렛의 위치를 중심으로 C와의 거리를 반지름으로 하는 원을 그린다.
결과적으로 우리가 찾아야 하는 것은 반지름이 𝑟₁ 인 A 와 반지름이 𝑟₂ 인 B 의 접점의 개수 라는 뜻이다.
그렇다면 두 원의 접점의 개수에 대해 경우의 수를 생각해보면 된다.
1. 두 원의 중심이 같고, 반지름도 같을 때 ( 접점의 개수가 무한할 때 )
𝑥₁ = 𝑥₂, 𝑦₁ = 𝑦₂, 𝑟₁ = 𝑟₂

가장 쉽게 먼저 찾을 수 있는 조건이다.
2. 접점이 없을 때
2-1 ) 두 점 사이의 거리가 각 원의 반지름의 합보다 클 때
( (𝑥₂ - 𝑥₁)² + (𝑦₂ - 𝑦₁)² )½ > 𝑟₁ + 𝑟₂
좀 더 쉽게 풀면 (𝑥₂ - 𝑥₁)² + (𝑦₂ - 𝑦₁)² > (𝑟₁ + 𝑟₂)²

2-1 ) 한 원 안에 다른 원이 있으면서 접점이 없을 때
이 부분에서 조금 어려워 하는 분들이 계신데 생각보다 어렵지 않다.
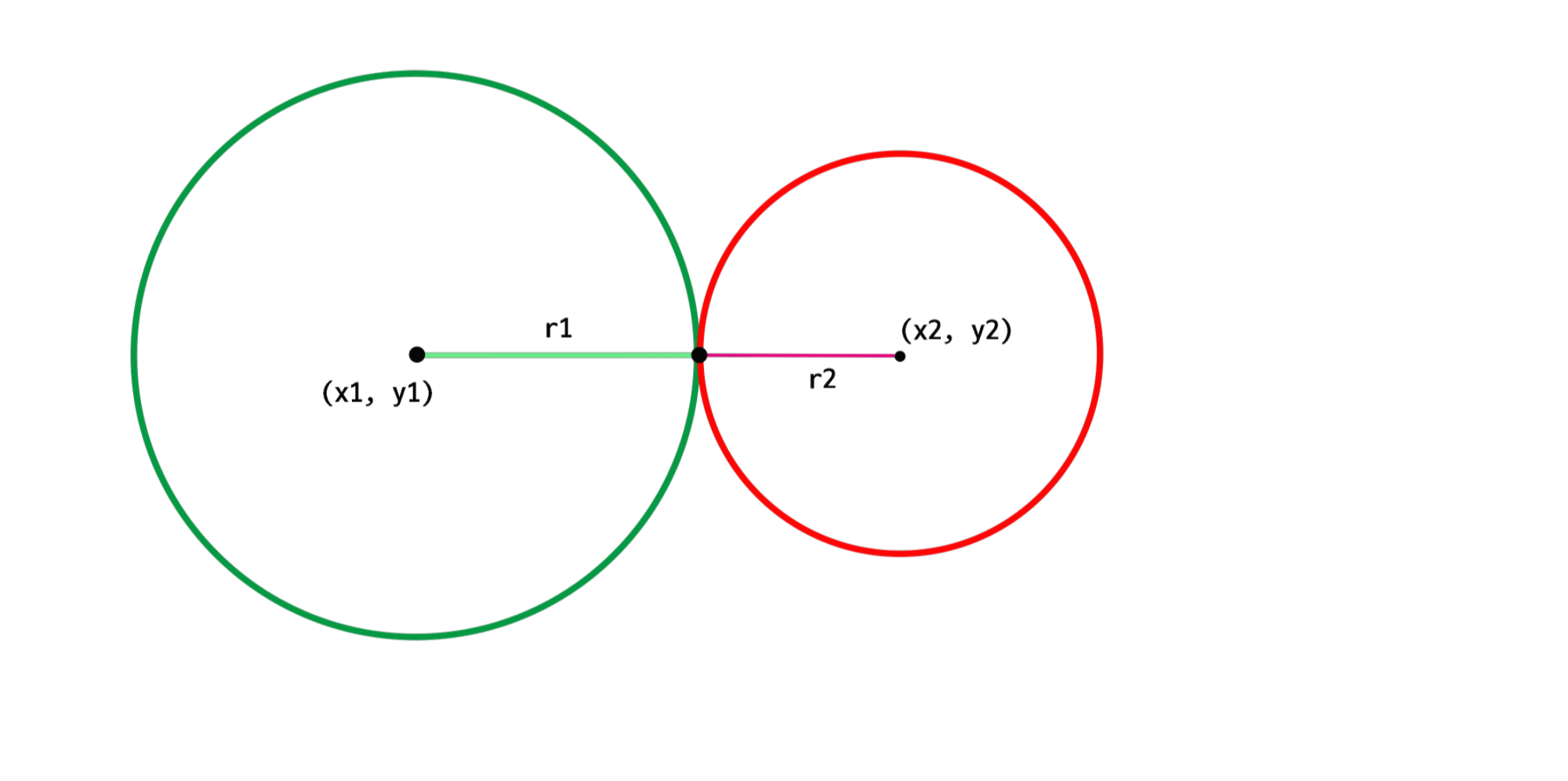
초록색 원과 빨간색 원이 아래와 같을 때, 접점을 갖지 않으려면 반지름이 같지 않으면서 반지름의 차가 두 원간의 중점 거리보다 크면 된다.
즉, 아래와 같은 식을 만족하면 된다.
( (𝑥₂ - 𝑥₁)² + (𝑦₂ - 𝑦₁)² )½ < ∣𝑟₂ - 𝑟₁∣
좀 더 쉽게 풀면 (𝑥₂ - 𝑥₁)² + (𝑦₂ - 𝑦₁)² < (𝑟₂ - 𝑟₁)²

3. 접점이 한 개일 때
3-1 ) 내접할 때
아까 위에서 원 안에 원이 있으면서 내접하지 않은 경우에서 조금만 생각해보면 바로 나온다.
바로 두 반지름의 차가 두 좌표간의 차랑 같으면 내접한다는 것이다.
( (𝑥₂ - 𝑥₁)² + (𝑦₂ - 𝑦₁)² )½ = ∣𝑟₂ - 𝑟₁∣
좀 더 쉽게 풀면 (𝑥₂ - 𝑥₁)² + (𝑦₂ - 𝑦₁)² = (𝑟₂ - 𝑟₁)²

3-2 ) 외접할 때
외접 할 때는 더 쉽다.
두 좌표간의 거리가 두 반지름의 합과 같으면 외접이다.
즉, 아래 공식을 만족하면 된다.
( (𝑥₂ - 𝑥₁)² + (𝑦₂ - 𝑦₁)² )½ = 𝑟₂ + 𝑟₁
좀 더 쉽게 풀면 (𝑥₂ - 𝑥₁)² + (𝑦₂ - 𝑦₁)² = (𝑟₂ + 𝑟₁)²
이렇게 조건을 다 찾으면 된다.
그리고 만약 위 조건에 만족하지 않는다면 당연히 접점은 두 개다.
그리고 추가로 좌표간의 거리, 즉 ( (𝑥₂ - 𝑥₁)² + (𝑦₂ - 𝑦₁)² )½ 을 구하기 위해 double 형으로 변수를 선언하여 아래와 같이 푸는 사람들이 많다.
double distance = Math.sqrt(Math.pow(x2 - x1, 2) + Math.pow(y2 - y1, 2));
그런데 좌표를 비교할 때 우리는 == 연산자를 써야하는데 double 형(또는 float형) 의 경우는 약간의 오차가 발생할 수 있다.
(아마 백준에서 이러한 케이스 입력이 없는 것인지 일단 풀리긴 하나, 절대 권장하는 방법이 아니다.)
이는 부동소수점 타입이 정확한 값이 아니라 근사치로 처리하기 때문이다.
이러한 특성으로 인해 조금의 오차가 있을 경우 두 실수는 같지 않을 수도 있다.
간단한 예로 0.1 + 0.2 == 0.3 참이 아니다.
못믿겠다면 아래 코드를 실행해보면 된다.
class Main {
public static void main(String[] args) {
double a = 0.1;
double b = 0.2;
double c = 0.3;
if(a + b == c) System.out.print("참입니다.");
else System.out.print("거짓입니다.");
}
}
실제로 돌려보면 아래와 같이 나온다.

그래서 이번에 풀이 하는 방법은 거리를 구할 때, Math.sqrt() 를 쓰는게 아니라 제곱되어있는 형태로
즉 (𝑥₂ - 𝑥₁)² + (𝑦₂ - 𝑦₁)² 을 쓰는 것이다.
그래서 필자가 경우의 수들마다 수식을 설명 할 때 쉽게 풀어쓴 이유도 위와 같은 이유 때문이다.
- 3가지 방법을 이용하여 풀이한다.
입력과 출력을 달리하여 풀어볼 것이다. 수식을 푸는 문제라 알고리즘 자체는 별로 고민할 것이 없다.
입력은 Scanner 와 BufferedReader 을 통한 방법으로 보여줄 것이며,
출력은 각 테스트케이스마다 출력하는 방법과 StringBuilder 을 써서 프로그램 종료 시점에 한 번에 출력하는 방법을 쓸 것이다.
- 풀이
- 방법 1
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int T = in.nextInt();
while (T-- > 0) {
int x1 = in.nextInt();
int y1 = in.nextInt();
int r1 = in.nextInt();
int x2 = in.nextInt();
int y2 = in.nextInt();
int r2 = in.nextInt();
System.out.println(tangent_point(x1, y1, r1, x2, y2, r2));
}
}
// 접점 개수 구하는 함수
public static int tangent_point(int x1, int y1, int r1, int x2, int y2, int r2) {
int distance_pow = (int)(Math.pow(x2 - x1, 2) + Math.pow(y2 - y1, 2)); // 중점간 거리 distance의 제곱
// case 1 : 중점이 같으면서 반지름도 같을 경우
if(x1 == x2 && y1 == y2 && r1 == r2) {
return -1;
}
// case 2-1 : 두 원의 반지름 합보다 중점간 거리가 더 길 때
else if(distance_pow > Math.pow(r1 + r2, 2)) {
return 0;
}
// case 2-2 : 원 안에 원이 있으나 내접하지 않을 때
else if(distance_pow < Math.pow(r2 - r1, 2)) {
return 0;
}
// case 3-1 : 내접할 때
else if(distance_pow == Math.pow(r2 - r1, 2)) {
return 1;
}
// case 3-2 : 외접할 때
else if(distance_pow == Math.pow(r1 + r2, 2)) {
return 1;
}
else {
return 2;
}
}
}
가장 기본적인 방법이라 할 수 있겠다.
알고리즘은 위에서 설명한 그대로 수식을 썼고, 해당 case 마다 접점의 개수를 return 을 해주면 된다.
참고로 무한대일 경우는 -1 을 출력하라고 백준에서 설명하고 있으니 이 점 유의하시길
- 방법 2
Scanner 대신 BufferedReader 을 쓰는 방법이다.
알고리즘 자체는 직전과 같고, 다만 BufferedReader 는 입력 메소드 readLine() 이 한 줄을 통째로 읽기 때문에 StringTokenizer 을 통해 문자열을 분리하고자 한다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int T = Integer.parseInt(br.readLine());
while (T-- > 0) {
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int r1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
int r2 = Integer.parseInt(st.nextToken());
System.out.println(tangent_point(x1, y1, r1, x2, y2, r2));
}
}
// 접점 개수 구하는 함수
public static int tangent_point(int x1, int y1, int r1, int x2, int y2, int r2) {
int distance_pow = (int)(Math.pow(x2 - x1, 2) + Math.pow(y2 - y1, 2)); // 중점간 거리 distance의 제곱
// case 1 : 중점이 같으면서 반지름도 같을 경우
if(x1 == x2 && y1 == y2 && r1 == r2) {
return -1;
}
// case 2-1 : 두 원의 반지름 합보다 중점간 거리가 더 길 때
else if(distance_pow > Math.pow(r1 + r2, 2)) {
return 0;
}
// case 2-2 : 원 안에 원이 있으나 내접하지 않을 때
else if(distance_pow < Math.pow(r2 - r1, 2)) {
return 0;
}
// case 3-1 : 내접할 때
else if(distance_pow == Math.pow(r2 - r1, 2)) {
return 1;
}
// case 3-2 : 외접할 때
else if(distance_pow == Math.pow(r1 + r2, 2)) {
return 1;
}
else {
return 2;
}
}
}
- 방법 3
입력에서는 BufferedReader 가 좋기에 입력 방법을 바꾸었다.
그런데 생각해보면 출력에서도 너무 반복적으로 출력하는 것 같단 생각이 들지 않는가?
그래서 출력할 문자열들을 하나로 묶어준 뒤, 프로그램 종료 시점에 한 번에 출력하는 방법으로 바꾸고자 한다.
위 방법을 이용하기 위해 StringBuilder 을 사용할 것이다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int T = Integer.parseInt(br.readLine());
while (T-- > 0) {
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int x1 = Integer.parseInt(st.nextToken());
int y1 = Integer.parseInt(st.nextToken());
int r1 = Integer.parseInt(st.nextToken());
int x2 = Integer.parseInt(st.nextToken());
int y2 = Integer.parseInt(st.nextToken());
int r2 = Integer.parseInt(st.nextToken());
sb.append(tangent_point(x1, y1, r1, x2, y2, r2)).append('\n');
}
System.out.println(sb);
}
// 접점 개수 구하는 함수
public static int tangent_point(int x1, int y1, int r1, int x2, int y2, int r2) {
int distance_pow = (int)(Math.pow(x2 - x1, 2) + Math.pow(y2 - y1, 2)); // 중점간 거리 distance의 제곱
// case 1 : 중점이 같으면서 반지름도 같을 경우
if(x1 == x2 && y1 == y2 && r1 == r2) {
return -1;
}
// case 2-1 : 두 원의 반지름 합보다 중점간 거리가 더 길 때
else if(distance_pow > Math.pow(r1 + r2, 2)) {
return 0;
}
// case 2-2 : 원 안에 원이 있으나 내접하지 않을 때
else if(distance_pow < Math.pow(r2 - r1, 2)) {
return 0;
}
// case 3-1 : 내접할 때
else if(distance_pow == Math.pow(r2 - r1, 2)) {
return 1;
}
// case 3-2 : 외접할 때
else if(distance_pow == Math.pow(r1 + r2, 2)) {
return 1;
}
else {
return 2;
}
}
}
앞으로도 문제를 풀 때 출력을 반복적으로 할 일이 많으면 StringBuilder 을 써주면서 출력할 문자를 하나로 묶어준 뒤 나중에 한 번에 출력하면 좋은 효율을 보일 것이다.
자세한 성능은 아래에서 보자.
- 성능

위에서 부터 순서대로
채점 번호 : 19596033 - 방법 3 : BufferedReader + StringBuilder
채점 번호 : 19596023 - BufferedReader
채점 번호 : 19596020 - Scanner
위 성능에서 보다시피 데이터가 충분히 많으면 많을수록 입력과 출력 방법만 바뀌어도 성능이 좋아진다는 것을 볼 수 있다.
- 정리
문제가 어렵지는 않았다.
다만 접점의 개수를 구하는데 각 경우의 수를 모두 찾아내야 하는데 이 부분에서 하나를 까먹거나 double 형의 문제점을 알고있지 못한다면 틀릴 수도 있다.
(다른 풀이를 보면 double 형으로도 풀리긴 하는 것 같긴 한데 아무래도 이러한 경우가 발생할 경우는 제외시킨건지... 여튼 double 형 연산은 매우 조심해서 다루어야 한다. 최대한 피할 수 있으면 피하는게 더 좋고..)
'JAVA - 백준 [BAEK JOON] > 기하 1' 카테고리의 다른 글
| [백준] 3053번 : 택시 기하학 - JAVA [자바] (4) | 2020.05.03 |
|---|---|
| [백준] 4153번 : 직각삼각형 - JAVA [자바] (3) | 2020.05.02 |
| [백준] 3009번 : 네 번째 점 - JAVA [자바] (2) | 2020.05.01 |
| [백준] 1085번 : 직사각형에서 탈출 - JAVA [자바] (2) | 2020.04.28 |