[백준] 4673번 : 셀프 넘버 - [C++]
https://www.acmicpc.net/problem/4673
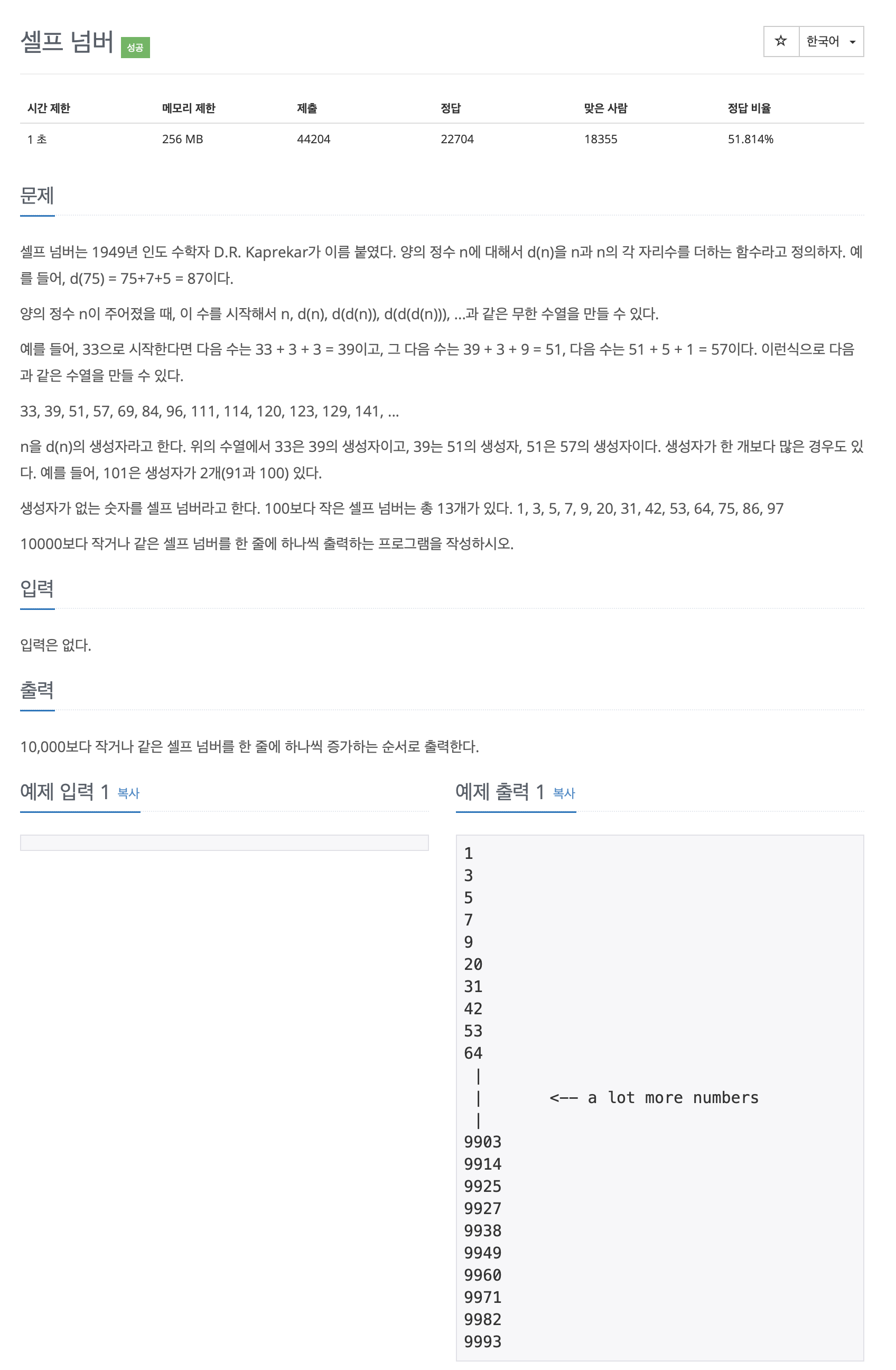
4673번: 셀프 넘버
셀프 넘버는 1949년 인도 수학자 D.R. Kaprekar가 이름 붙였다. 양의 정수 n에 대해서 d(n)을 n과 n의 각 자리수를 더하는 함수라고 정의하자. 예를 들어, d(75) = 75+7+5 = 87이다. 양의 정수 n이 주어졌을 때,
www.acmicpc.net
- 문제
※ 주의할 점
- 한 줄에 하나씩 출력해야한다. 그렇다고 a lot more numbers 문자를 출력하는 것은 절대 아니다.
- 양의 정수. 즉 0보다 크고 10000 보다 작거나 같은 수 중에 셀프 넘버(self number) 을 출력하면 된다.
- 알고리즘 [접근 방법]
먼저 설명하기에 앞서 함수를 굳이 쓰지 않아도 된다. 그러나 함수 카테고리인 만큼 함수를 이용하여 풀어보고자 한다. 그러니 만약 코드를 보고 함수를 쓰고싶지 않다면 쓰지 않고 해도 백준에서는 출력값만 맞으면 성공으로 되니 독자들의 판단하에 선택하면 된다.
그럼 먼저 셀프 넘버 알고리즘을 구현해보자.
구현 방식은 1 부터 10000까지 검사한 뒤, 해당 수를 생성자로 하는 수가 있으면 그 수를 거르는 것이다.
먼저 함수는 아래와같이 짠다.
int d(int number) { // 함수 d
}
int main(int argc, char const *argv[]) {
for (int i = 1; i < 10001; i++) {
int n = d(i);
}
return 0;
}
1 부터 10000까지 검사할 때 메인에서 d 함수로 숫자를 넣어보며 return 되는 수는 해당 number를 생성자로 하는 수로 구성 할 것이다.
그럼 d 함수를 좀 더 구체적으로 작성해보자.
1. 먼저 number 라는 수를 받게되면 number 을 생성자로 하는 수를 리턴시킬 것이기 때문에 sum 이란 변수를 하나 생성한다.
그리고 초기 값은 number 로 한다. (이후 과정에서 왜 number 로 초기화 하는지 알려줄 것이다.)
int d(int number) {
int sum = number;
}
2. 셀프넘버를 찾기 위한 반복문을 작성해준다.
int d(int number) {
int sum = number;
while(number != 0) {
}
}
일단 각 자리수를 더해주기 위해서 나머지 연산자와 나눗셈 연산자로 10 단위씩 number 을 줄여 갈 것이기 때문에 number 가 0 이 아닐 때 까지 계속 반복해준다.
3. number 의 첫 번째 자리수를 구하기 위해 % 연산자를 사용하여 sum 에 더해주고, 이후 / 로 10을 줄인다.
int d(int number) {
int sum = number;
while(number != 0) {
sum = sum + (number % 10); // 첫 째 자리수
number = number / 10; // 10을 나누어 첫 째 자리를 없앤다.
}
return sum;
}즉, 위 알고리즘 대로 한다면 아래와 같다.
1234 라는 수가 들어왔다고 가정하자. (number = 1234)
그럼 1234 라는 수를 생성자로 하는 수는 다음과 같다.
1234 + 1 + 2 + 3 + 4 = 1244
즉 sum 에 먼저 1234 라는 수를 선언과 함께 초기화 시켜주었고, 다음 반복문부터 각 자리수를 더해주는 방식인 것이다.
[반복문]
첫 번째 반복 )
number % 10 = 4 이므로 sum 에 4 가 더해져 sum 은 1238 이 된다.
number / 10 = 123 이고 이 수가 새로운 number 가 된다. 즉 number = 123 이 된다.
두 번째 반복 )
number % 10 = 3 이므로 sum 에 3 이 더해져 sum 은 1241 이 된다.
number / 10 = 12 이고 이 수가 새로운 number 가 된다. 즉 number = 12 가 된다.
세 번째 반복 )
number % 10 = 2 이므로 sum 에 2 가 더해져 sum 은 1243 이 된다.
number / 10 = 1 이고 이 수가 새로운 number 가 된다. 즉 number = 1 이 된다.
네 번째 반복 )
number % 10 = 1 이므로 sum 에 1 이 더해져 sum 은 1244 가 된다.
number / 10 = 0 이고 이 수가 새로운 number 가 된다. 즉 number = 0 이 된다.
이후 while 조건문에 의해 number 가 0 이므로 반복문을 탈출한다.
그리고 sum 을 return 해주면 된다.
4. return 된 수는 생성자가 있는 수, 즉 출력하면 안되는 수 이므로 boolean 배열을 통해 true 로 바꾸어 준다.
int d(int number) {
int sum = number;
while (number != 0) {
Psum = sum + (number % 10); // 첫 째 자리수
number = number / 10; // 10을 나누어 첫 째 자리를 없앤다.
}
return sum;
}
int main(int argc, char const *argv[]) {
bool check[10001]{ false };
for (int i = 1; i < 10001; i++) {
int n = d(i);
if (n < 10001) { // 10000 이 넘는 수는 필요가 없다.
check[n] = true
}
}
return 0;
}즉, 메인에서 보면 d 함수에 의해 리턴된 수 n 을 boolean 배열의 인덱스로 사용하여 해당 위치를 true 로 바꾸어 주는 것이다.
이때 문제에서 나와있듯이 1 부터 10000까지이므로 10001 이상의 수는 필요 없다.
위 과정이 끝나면 마지막으로는 boolean 배열에서 false 인 원소의 위치(인덱스)를 출력해주면 된다.
- 2가지 방법을 사용하여 풀이한다.
이 번 문제의 경우 입력은 따로 없고 정해진 답을 출력하는 것이기 때문에 한 가지 풀이만 하겠다.
- 풀이
#include <iostream>
using namespace std;
int d(int number) {
int sum = number;
while (number != 0) {
sum = sum + (number % 10); // 첫 째 자리수ˇ
number = number / 10; // 10을 나누어 첫 째 자리를 없앤다.
}
return sum;
}
int main(int argc, char const *argv[]) {
bool check[10001] = { false, };
for (int i = 1; i < 10001; i++) {
int n = d(i);
if (n < 10001) { // 10000 이 넘는 수는 필요가 없다.
check[n] = true;
}
}
for (int i = 1; i < 10001; i++) {
if (!check[i]) {
cout << i << "\n";
}
}
return 0;
}
그렇게 크게 바뀌는 것도 없고 어렵지는 않을 것이다.
- 성능

채점 번호 : 41700479 - 방법 1
- 정리
이 번 문제는 크게 어렵지는 않았을 것이다.
여담으로 개인 사정이 있어 매우 바쁜 나날을 보내왔기에... 최근 포스팅을 올리지 못했었다. 그래도 이제는 조금은 여유가 생겨 차근차근 다시 정리해나가고자 한다.
그 동안 댓글에 대한 답변밖에 드리지 못했는데, 많은 분들이 꾸준히 찾아주셔서 정말 감사하다는 말씀 드리고 싶다.
만약 어렵거나 이해가 안되는 부분이 있다면 언제든 댓글 남겨주시기를 바란다.
'C++ - 백준 [BAEK JOON] > 함수' 카테고리의 다른 글
| [백준] 1065번 : 한수 - [C++] (0) | 2022.04.12 |
|---|---|
| [백준] 15596번 : 정수 N개의 합 - [C++] (2) | 2022.01.08 |