[백준] 11047번 : 동전 0 - JAVA [자바]
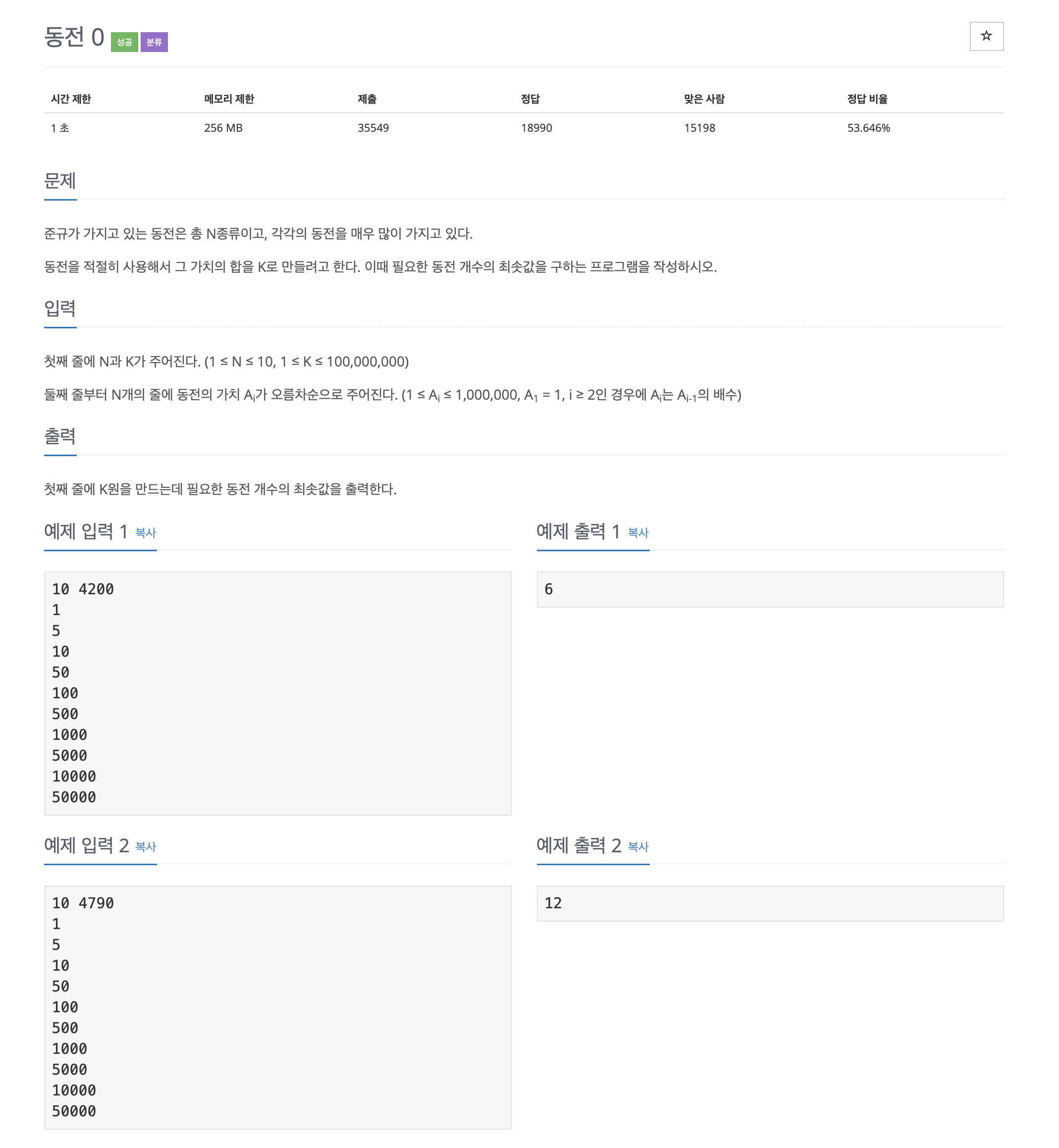
11047번: 동전 0
첫째 줄에 N과 K가 주어진다. (1 ≤ N ≤ 10, 1 ≤ K ≤ 100,000,000) 둘째 줄부터 N개의 줄에 동전의 가치 Ai가 오름차순으로 주어진다. (1 ≤ Ai ≤ 1,000,000, A1 = 1, i ≥ 2인 경우에 Ai는 Ai-1의 배수)
www.acmicpc.net
-
문제
그리디 알고리즘의 첫 문제다. 사실 그리디 알고리즘이 무엇인지는 몰라도 쉽게 풀 수 있는 문제지만, 일단 그리디 알고리즘에 대해 알고가도록 하자.
- 알고리즘 [접근 방법]
1. 그리디 알고리즘 (Greedy Algorithm)
먼저 그리디 알고리즘이 뭔지 알아보자. 그리디 알고리즘이란, 말 그대로 greedy, 즉 탐욕 알고리즘이다. 왜 탐욕 알고리즘일까? 그리디 알고리즘에서 가장 중요한 키워드는 '매 번의 선택에서 가장 좋아보이는 선택을 하여 적절한 답을 찾아간다'는 것이다.
역시 말로 설명하기는 어려우니 그림으로 설명해보도록 하겠다.
일단 여행을 떠나보자. 서울에서 출발하여 부산을 가려 한다. 그리고 다음 사진과 같이 경로들이 있고 각 경로에 따른 소요 시간이 적혀있다.
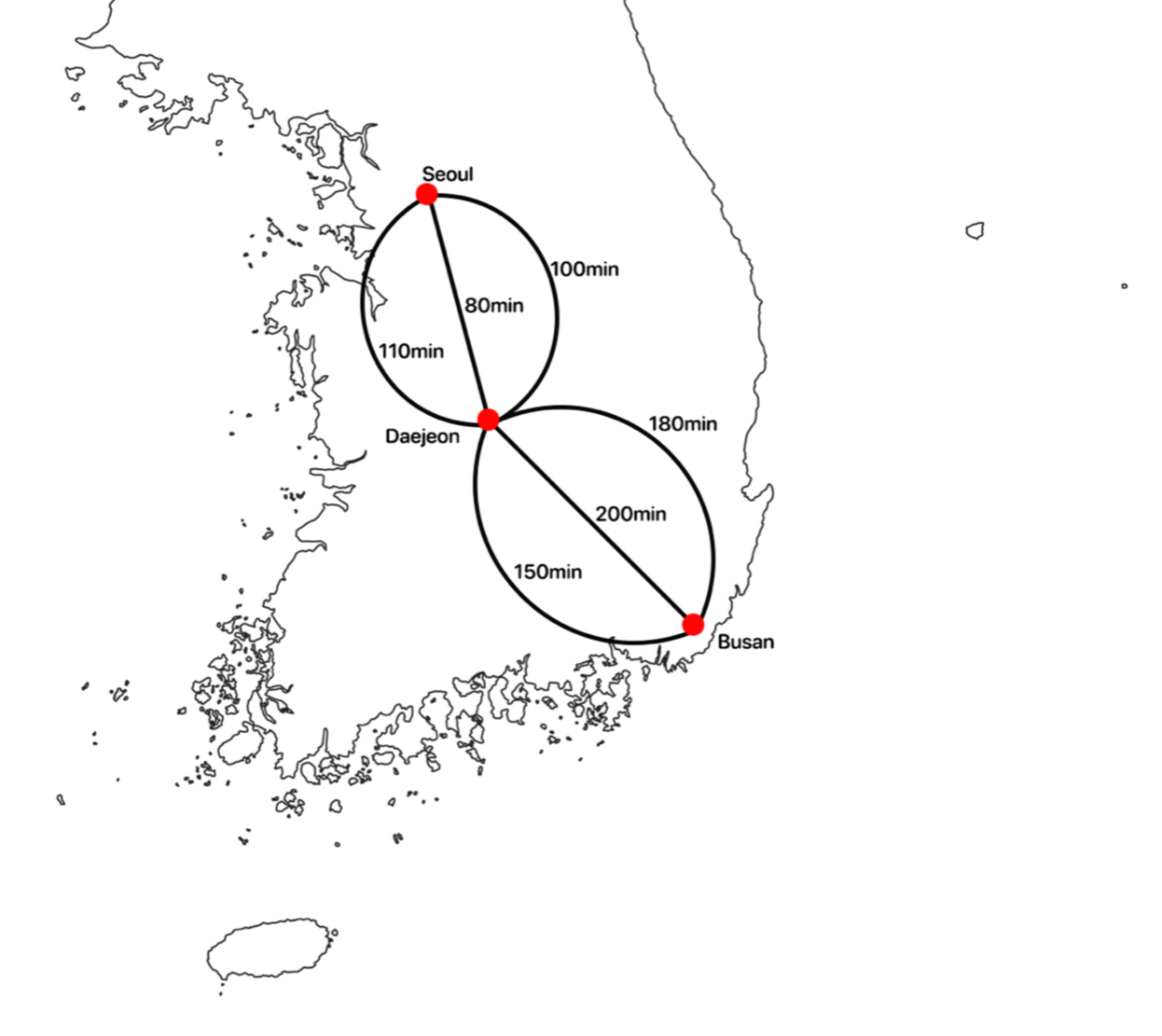
그리고 여러분들이 최대한 빠르게 서울에서 부산까지 가고싶을 때 어떻게 선택할까?
먼저 서울에서 대전을 가는 경로는 3개가 있다. 이 중 가장 적게 소요되는 경로의 경우 80분이 걸린다고 한다. 당연 빠르게 가려면 80분짜리 경로를 선택 할 것이다.
그 다음 대전에서 부산으로 가는 경로도 3개가 있다. 이 세 개중 150분이 걸리는 경로가 가장 시간이 적게 소요된다. 즉, 전체 루트로는 서울-대전 : 80분, 대전-부산 : 150분이라는 시간으로 총 230분(3시간 50분)이 걸린다.
이렇게 '각 단계별로 최선의 선택지를 선택'하는 것이 바로 그리디 알고리즘이다.
이 알고리즘은 꽤 좋아보이지만 여러분이 명심해야 할 것은 '그리디 알고리즘은 항상 최적의 해를 도출해내는 것은 아니다.'라는 것이다. 위 지도에서 새로 도로가 건설되어 다음과 같은 루트가 새로 생겼다고 해보자.

만약 그리디 알고리즘대로 한다면 각 순간 별 최적의 선택을 해야하니, 서울에서 이동하는 경로 중 가장 적게소요되는 '대전으로 가는 80분짜리 경로'를 선택한 뒤, 대전에서 부산으로 가는 경로 중 가장 적게 소요되는 '150분짜리 경로'를 선택하게 될 것이다.
하지만, 실제로는 서울에서 원주를 거쳐 부산으로 가는 길이 130분 + 90분 = 220분(3시간 40분)으로 앞선 240분(3시간 50분)보다 더욱 빨리 도착할 수 있다.
이런식으로 그리디 알고리즘은 '최적해에 근사하는 방법'인 것일뿐 항상 최적해를 만족하는 것이 아니다.
그리디 알고리즘이 잘 활용 될 수 있는 문제들은 대개 특징이 있는데, 1)이전의 탐욕 선택이 이후의 선택에 영향을 주지 않는다(독립적)는 점과 2)전체 최적해가 부분 문제에 대해서도 최적해를 만족한다는 것이다.
첫 번째 이미지에서는 서울에서 부산으로 이어지는 경로는 서울-대전-부산 경로밖에 없다. 즉, 서울-대전과 대전-부산의 경로는 각 독립적이기 때문에 서울-대전 경로에서 어떤 것을 선택하느냐에 따라서 대전-부산 경로의 선택에 영향을 미치지 않는다. 즉, 일단 첫 번째 조건을 만족한다.
또한 각 도시별 경로는 독립적이기 때문에 결과적으로 서울-대전의 최적해는 곧 전체 최적해의 부분 문제가 되고, 대전-부산의 최적해 또한 마찬가지다. 즉, 각 부분 문제의 최적해는 전체 문제의 최적해이자, 반대로 말하면 전체 최적해가 부분 문제에 대해서도 최적해를 만족한다는 것이다.
두 번째 이미지에서는 그럼 왜 최적해를 만족하지 못할까?
일단 서울에서 부산을 가는 도중 두 가지 도시로 나뉜다. 서울-대전을 잇는 경로와 서울-원주를 잇는 경로로 나뉘게 된다. 그렇게 되면, 이후 선택지는 대전-부산 또는 원주-부산경로로 나뉘게 되는데, 이는 처음 선택했던 경로에 따라 결정할 수 있는 경로에 영향을 미치기 때문에 독립적이지 않게 된다. 결과적으로, 독립적이지 않다는 것은 전체 최적해에 대해 부분 문제 또한 독립적이지 않아 항상 최적해를 만족하지 않는다까지 이어질 수 있다.
물론 장점은 뚜렷하다. 동적계획법과 달리 최적해를 100% 보장해주진 못하지만 각 순간별 최적 선택을 하기 때문에 근사 해를 구하는 속도가 매우 빠르다는 것이다. 그래서 동적계획법과 그리디 알고리즘은 서로 상호보완하여 같이 쓰이기도 한다. 예로들어 위의 두 번째 지도 이미지보다 더욱 많은 경로들이 있을 때 일정 구간을 분기점으로 두고 그 안에서는 동적계획법을 통해 가장 빠른 루트를 구하여 가는 방식이 있다.
그러면 대표적인 문제들은 무엇인가? 라는 물음이 나올 것이다.
대표적으로 거스름 돈 문제나 활동 선택, 최소 신장 트리 문제들이 대표적이다. 이 문제들은 그리디 알고리즘 포스팅을 하면서 차근차근 알게 될 것이다.
2. 동전 0 문제 알고리즘
그럼 문제로 돌아와서 알고리즘을 한 번 보도록 하자.
위 문제를 보면 각 동전들은 '서로 배수 관계에 있다'는 것을 볼 수 있다. 5는 1의 배수이고, 10은 5의 배수이고, ... 이렇게 모든 동전들은 서로 배수관계에 놓여있다. 이렇게 배수관계에 놓여있을 경우 풀리는 대표적인 문제가 바로 거스름돈 문제와 이번 문제와 같은 것들이다.
(실제로 화폐를 제작할 때에도 대부분 이런 식으로 배수관계가 되도록 한다고 한다.)
그럼 그리디 알고리즘을 어떻게 적용할 수 있을까?
아까 말했던 것처럼 '최적해'를 찾아 나가는 것이다. K원을 만들 때 최소한의 개수를 이용해야 하니 당연하게도 가장 큰 가치를 지닌 동전부터 선택하는 것이 당연할 것이다.
즉, N개의 동전 중 가장 큰 가치를 지닌 동전부터 탐색하여 동전의 가치가 K보다 클 경우는 넘어가고, 아닐경우는 최대 구성 가능한 개수를 더해주면 된다.
int[] coin = new int[N]; // 동전 가치가 입력되었다고 가정
int count = 0;
for(int i = N - 1; i >= 0; i--) {
// 현재 동전의 가치가 K보다 작거나 같아야지 구성가능하다.
if(coin[i] <= K) {
// 현재 가치의 동전으로 구성할 수 있는 개수를 더해준다.
count += (K / coin[i]);
K = K % coin[i];
}
}
매우 쉽지 않은가?
그리디 알고리즘 장점 중 하나가 동적계획법보다 코드가 간결해지는 것도 있다. 만약 동적계획법으로 풀었다면 결과는 같았더라도 중첩탐색이 이루어지기 때문에 결과적으로 시간이 더욱 오래걸렸을 것이다.
그럼 이를 바탕으로 전체 코드를 보자.
- 2가지 방법을 사용하여 풀이한다.
이번 문제는 크게 비교할 것은 없어서 Scanner와 BufferedReader를 통한 입력방법에 따른 성능비교를 할 것이다.
1 . Scanner
2. BufferedReader
- 풀이
- 방법 1 : [Scanner + StringBuilder]
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
int K = in.nextInt();
int[] coin = new int[N];
for(int i = 0; i < N; i++) {
coin[i] = in.nextInt();
}
int count = 0;
for(int i = N - 1; i >= 0; i--) {
// 현재 동전의 가치가 K보다 작거나 같아야지 구성가능하다.
if(coin[i] <= K) {
// 현재 가치의 동전으로 구성할 수 있는 개수를 더해준다.
count += (K / coin[i]);
K = K % coin[i];
}
}
System.out.println(count);
}
}
가장 기본적인 방법이라 할 수 있겠다.
- 방법 2 : [BufferedReader + StringBuilder]
입력 방법을 Scanner 대신 BufferedReader 을 사용하여 풀이하는 방법이다. 단, BufferedReader 는 문자열을 한 줄로 읽기 때문에 N과 K를 구분하기 위해 공백을 기준으로 문자열을 분리해주어야하니 StringTokenizer 을 사용하여 풀도록 하겠다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int[] coin = new int[N];
for(int i = 0; i < N; i++) {
coin[i] = Integer.parseInt(br.readLine());
}
int count = 0;
for(int i = N - 1; i >= 0; i--) {
// 현재 동전의 가치가 K보다 작거나 같아야지 구성가능하다.
if(coin[i] <= K) {
// 현재 가치의 동전으로 구성할 수 있는 개수를 더해준다.
count += (K / coin[i]);
K = K % coin[i];
}
}
System.out.println(count);
}
}
- 성능

채점 번호 : 22831962 - 방법 2 : BufferedReader
채점 번호 : 22831950 - 방법 1 : Scanner
입력의 경우 확실히 Scanner 보다는 BufferedReader 가 빠른 걸 볼 수 있다.
- 정리
이 문제는 아마 대부분 쉽게 풀었을 것이다. 그대신 그리디 알고리즘에 대해 좀 더 알아갈 수 있도록 하기 위해 그리디 알고리즘 설명을 추가하였다. 많은 분들이 찾아보았으면 좋겠다만, 문제가 워낙 쉬웠던터라..
'JAVA - 백준 [BAEK JOON] > 그리디 알고리즘' 카테고리의 다른 글
| [백준] 13305번 : 주유소 - JAVA [자바] (26) | 2021.01.13 |
|---|---|
| [백준] 1541번 : 잃어버린 괄호 - JAVA [자바] (12) | 2020.10.08 |
| [백준] 11399번 : ATM - JAVA [자바] (8) | 2020.10.07 |
| [백준] 1931번 : 회의실배정 - JAVA [자바] (44) | 2020.10.05 |